В.П. Пинчук
Анализ и построение алгоритмов и структуры данных для спец. КСС. -
Запорожье: ЗНТУ, 2010.
Анализ алгоритмов сортировки и поиска
1. Алгоритмы поиска
2. Сортировка методом парных перестановок
3. Метод пузырька
4. Метод вставки
5. Метод слияния
6. Метод вычерпывания
7. Результаты тестирования
Алгоритмы поиска
Задача
Дано: одномерный массив А размером n и искомое значение key.
Требуется: определить, содержит ли массив А значение key и, если да, то получить номер соответствующего элемента массива А.
Поиск в неупорядоченном массиве (последовательный поиск)
Достоинством алгоритма последовательного поиска является то, что он работает на неупорядоченных последовательностях. Недостаток - невысокая эффективность, алгоритм имеет линейный порядок, асимптотический класс O(n).
Искомое значение key последовательно сравнивается с элементами массива А. Наихудший случай будем иметь, когда искомое значение отсутствует в массиве, наилучший – когда искомое значение совпадает с первым элементом массива. Отсюда:
t £ Const×n,
или t = f(n) = O(n).
Т.о. рассматриваемый алгоритм является линейным по времени.
Поиск в упорядоченном массиве. Алгоритм бинарного поиска
Алгоритм бинарного поиска применим в случае, когда последовательность предварительно упорядочена. Ниже приведен пример функции, выполняющей бинарный поиск для массива, упорядоченного по возрастанию.
int b_find(int* A, int n, int key) // key – искомое значение
{ int p = 0, q = n-1, k; // [p,q] – отрезок массива
while (q >= p) { k = p + (q-p)/2; // k – номер среднего эл-та
if (A[k] == key) return k;
if (A[k] < key) p = k + 1;
else q = k - 1;
}
Return -1; // значение key не найдено
}
На каждом шаге этого алгоритма текущий отрезок массива делится на две части, размеры которых отличаются не более чем на единицу. Размер текущего отрезка массива на каждом шаге уменьшается в 2 раза (даже немного больше, чем в 2 раза, т.к. средний элемент на каждом шаге выбывает). Процесс завершается, когда размер очередного отрезка массива оказывается равным единице. Отсюда время будет равно:
t £ Const×log2(n).
Отсюда: t = f(n) = O(log2(n)).
Результаты прямых экспериментов
Абсолютное время решения задачи поиска для n = 100 000 000 (худший случай, процессор E8400):
последовательный поиск: 80650 мкс
бинарный поиск: 3 мкс
Задачи сортировки. Сортировка методом парных перестановок
Алгоритмы решения задачи сортировки лежат в основе многих приложений (особенно следует отметить базы данных и экспертные системы). Задача поиска элемента с заданным значением решается намного быстрее, если массив предварительно упорядочен.
Назовем некоторые основные методы решения задачи сортировки:
- метод пузырька (существуют разные модификации);
- метод вставки;
- метод слияния.
Для представления алгоритмов будем использовать язык С++. Напомним, что, согласно правилам этого языка, элементы массива, имеющего n элементов имеют номера от 0 и до n-1.
Метод парных перестановок
Основой этого алгоритма является операция парного упорядочивания (упорядочивание пары соседних элементов массива). Пары упорядочиваются последовательно, начиная с первой пары (элементы с номерами 0, n-1) и до последней (элементы с номерами n-2, n-1). Для того, чтобы гарантировать полное упорядочивание любого массива, необходимо выполнить n-1 проходов парного упорядочивания. Таким образом, алгоритм содержит двойной цикл. Ниже представлен фрагмент программы, выполняющий сортировку массива A размером n элементов по убыванию.
Рассматриваем направление сортировки - по возрастанию.
void sort_pair(int* A, int n)
{ int i, k;
for (i = 0; i < n - 1; i++) // множитель n-1
for (k = 0; k < n - 1; k++) // множитель n-1
if (A[k] > A[k+1]) swp(A[k], A[k+1]); // время = с
}
Здесь swp(x,y) - процедура парного обмена (кстати, это реальная функция из модуля syst.h).
Вложенные циклы не зависимы друг от друга. Поэтому:
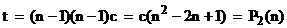 .
.
Отсюда, на основании базовой теоремы 1, получаем:
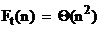 .
.
Метод пузырька
В следующем варианте метода пузырька, алгоритм построен несколько иначе. Вначале среди всех элементов массива находится наибольший и, затем, этот элемент меняется местами с первым элементом массива. На следующем шаге выполняется такая же процедура с отрезком массива "второй элемент - последний элемент". Работа алгоритма завершается после обработки отрезка массива "предпоследний элемент - последний элемент".
Программная реализация алгоритма:
void sort_bubble(int* A, int n)
{ int i, j, im;
for (i = 0; i < n-1; i++) // суммировать по i от 0 по n-2
{ im = i; // время = c1
for (j = i+1; j < n; j++) // множитель n-i-1
if (A[j] > A[im]) im = j; // время = c2 , худший случай
swp(A[im], A[i]); // время = c3
}
}
Время работы алгоритма можно еще немного уменьшить, если в отрезке массива определять наибольший и наименьший элементы и перемещать их в первую и последнюю позиции отрезка массива соответственно.
Здесь внутренний цикл зависим от внешнего. Оцениваем худший случай. Общее время работы процедуры будет равно:
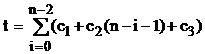 .
.
Отсюда:
 .
.
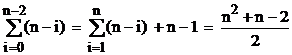 .
.
И тогда:
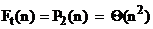 .
.