Шифр
Проверил:.
Ухта 2009 г.
Содержание.
| 1. | Задание на выполнение контрольной работы……………... | |
| 2. | Решение, расчет передаточной функции………………….. | |
| 3. | С помощью критерия устойчивости Гурвица…………… | |
| 4. | С помощью критерия устойчивости Рауса………………. | |
| 5. | С помощью критерия устойчивости Михайлова………… | |
| 6. | С помощью критерия устойчивости Найквиста…………. | |
| 7. | По логарифмическим частотным характеристикам………. | |
| 8. | Меры по обеспечению устойчивости………………………. |
Контрольная работа №2.
Задание на выполнение контрольной работы.
Вариант №1
Исследовать систему автоматического управления, представленную структурной схемой на устойчивость:
1. С помощью критерия устойчивости Гурвица
2. С помощью критерия устойчивости Рауса
3. С помощью критерия устойчивости Михайлова
4. С помощью критерия устойчивости Найквиста
5. По логарифмическим частотным характеристикам.
В случае, если система неустойчива, предложить меры по обеспечению устойчивости.
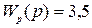 ;
; 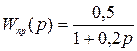 ;
;  ;
; 
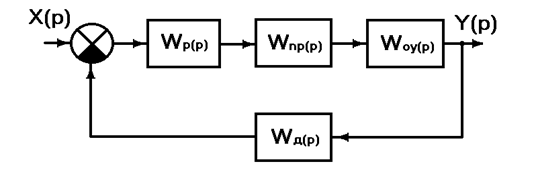 |
Решение:
Найдем передаточную функцию W(p).

где:
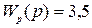 ;
;
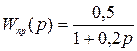 ;
;
 ;
;

Подставив значения получим:
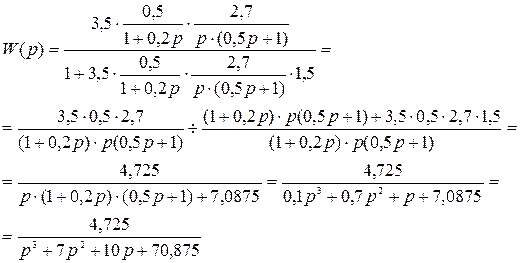
Исследуем систему на устойчивость с помощью критерия Гурвица.
Этот критерий является алгебраическим. Если задана передаточная функция системы W(p) = B(p) / A(p), то для получения характеристического уравнения надо приравнять к нулю ее знаменатель

Порядок составления матрицы Гурвица следующий. В левом верхнем углу матрицы записывается коэффициент  . По главной диагонали располагаются коэффициенты характеристического уравнения по мере убывания индексов. Над элементами главной диагонали записываются коэффициенты по убыванию индексов, под элементами - по возрастанию индексов. Там, где индекс больше n или меньше нуля, записываются нули.
. По главной диагонали располагаются коэффициенты характеристического уравнения по мере убывания индексов. Над элементами главной диагонали записываются коэффициенты по убыванию индексов, под элементами - по возрастанию индексов. Там, где индекс больше n или меньше нуля, записываются нули.
Далее надо вычислить определители Гурвица, которые получают из матрицы путем отчёркивания равного числа строк и столбцов в левом верхнем углу матрицы.
Из коэффициентов характеристического уравнения составим сначала главный определитель Гурвица:

диагональные миноры:

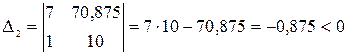 .
.
 < 0.
< 0.
Критерий устойчивости Гурвица формулируется следующим образом: система устойчива, если все определители Гурвица больше нуля, т. е.  Так как миноры матрицы меньше нуля, следовательно, система не устойчива.
Так как миноры матрицы меньше нуля, следовательно, система не устойчива.
Исследуем систему на устойчивость методом Рауса.
Составим таблицу:
В первой строке таблицы записываем в порядке возрастания индексов коэффициенты характеристического уравнения, имеющие четный индекс; а0,а2,а4, и т.д.; во второй строке - коэффициенты характеристического уравнения, имеющие нечетный индекс; а1,а3,а5.

| 
| ||
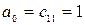
| 
| ||

| 
| ||
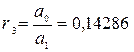
| с13 = а2 – r3а3= =-0,125 | ||
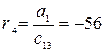
| с14 = а3 – r4с23= =70,875 |
Из таблицы видно, что система будет неустойчивой, так как в колонке “1” есть отрицательное число, а именно с13 = -0,125. А условие устойчивости Рауса формулируется так: д ля того, чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак.
Критерий устойчивости Михайлова
В отличие от алгебраического критерия Гурвица, этот критерий является частотным. Он основан на построении годографа характеристического вектора  Годографом называется кривая, прочерчиваемая концом вектора
Годографом называется кривая, прочерчиваемая концом вектора  на комплексной плоскости при изменении частоты
на комплексной плоскости при изменении частоты  от 0 до
от 0 до  . Характеристический вектор
. Характеристический вектор  получается из характеристического уравнения путем замены
получается из характеристического уравнения путем замены  на
на 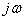 .
.
Критерий устойчивости Михайлова формулируется следующим образом: система устойчива, если годограф характеристического вектора, начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении n квадрантов, где n - порядок характеристического уравнения системы.

Характеристический вектор  можно представить в виде:
можно представить в виде:


где  - действительная, а
- действительная, а  - мнимая часть вектора
- мнимая часть вектора 
Действительная часть:


Корни уравнения:


Мнимая часть:
V = - 1 w 3 + 10 w = - w (1 w 2 -10)
- w (1 w 2 - 10) = 0
Корни уравнения:
w3 = 0.
Годограф Михайлова. 
Система не устойчива.
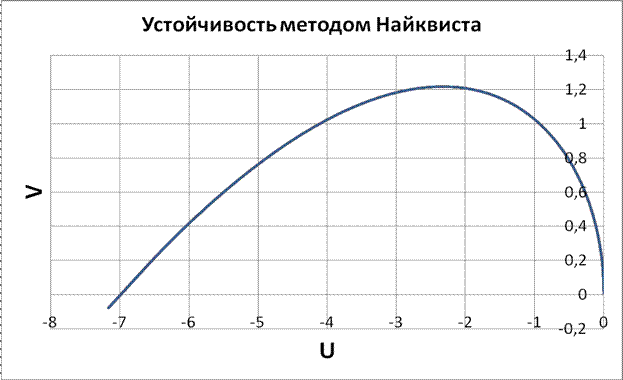
С помощью критерия устойчивости Найквиста
Критерий устойчивости Найквиста - один из способов судить об устойчивости замкнутой системы управления - по её разомкнутой АФЧХ. Является одним из частотных критериев устойчивости. С помощью этого критерия оценить устойчивость весьма просто, без необходимости вычисления полюсов передаточной функции замкнутой системы.
Так же, как и критерий Михайлова, критерий Найквиста является частотным. Он основан на построении годографа передаточной функции H(j  ) разомкнутой системы. Критерий устойчивости Найквиста формулируется следующим образом: замкнутая система устойчива, если годограф передаточной функции H(j
) разомкнутой системы. Критерий устойчивости Найквиста формулируется следующим образом: замкнутая система устойчива, если годограф передаточной функции H(j  ) разомкнутой системы не охватывает на комплексной плоскости точку с координатами (-1, j0).
) разомкнутой системы не охватывает на комплексной плоскости точку с координатами (-1, j0).
Вид разорванной предложенной системы,

Найдем передаточную функцию W(p).
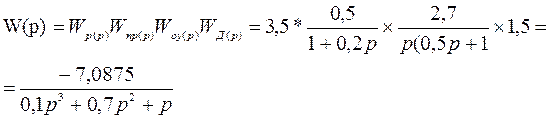
Выделим мнимую и действительную части:


V = - 0,1j w 3 + w
В результате получаем не устойчивую систему, так как кривая охватывает точку (-1;0).
Проверим разомкнутую систему на устойчивость методом Рауса.

Составим таблицу:

| 
| ||

| 
| ||

| |||
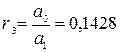
| с13 = а2 – r3а3= =1 | ||

| с14 = а3 – r4с23= =0 |
Так как С13=0 система находится на границе устойчивости (неопределенная).