Урок
Тема:Взаимное расположение двух прямых в пространстве.
Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми
Цель работы: Обобщить и систематизировать знания по теме «Взаимное расположение
прямых и плоскостей»; закрепить умения использовать полученные знания для решения
задач
Ход урока
Вопросы для рассмотрения
| 1.Взаимное расположение двух прямых в пространстве |
| 2.Признак скрещивающихся прямых |
| 3.Угол между скрещивающимися прямыми |
Взаимное расположение двух прямых в пространстве
Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Определение |
| Две пересекающиеся прямые | 
| Две прямые называют пересекающимися прямыми, если они имеют единственную общую точку. |
| Две параллельные прямые | 
| Две прямые называют параллельными прямыми, если они лежат в одной плоскости и не имеют общих точек |
| Две скрещивающиеся прямые | 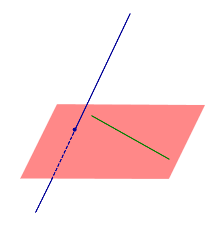
| Две прямые называют скрещивающимися прямыми, если не существует плоскости, содержащей обе прямые. |
С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.
| Фигура | Рисунок | Тип утверждения и формулировка |
| Две различные точки | 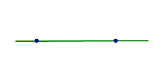
| Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия. |
| Прямая линия и точка, не лежащая на этой прямой | 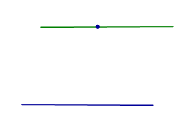
| Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой. |
| Две пересекающиеся прямые | 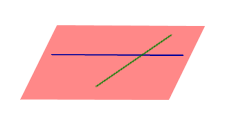
| Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
| Две параллельные прямые | 
| Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
Признак скрещивающихся прямых
Признак скрещивающихся прямых. Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).
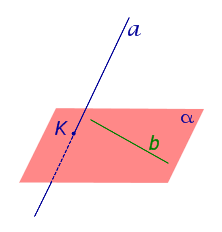
Рис.1
Доказательство. Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».
Для этого предположим, что прямая a, пересекающая плоскость в точке K, и прямая b, лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α. Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K, не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости. Мы получили противоречие с тем, что по условию прямая a пересекает плоскость, а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.