Направление «Строительство» бакалавры 2020-2021 учебный год.
Практические занятия IкурсеII семестр, д/о (1ч лек.+2 часа практ.)
Занятие 1. Методы интегрирования дифференциальных уравнений 1-го
порядка. Дифференциальные уравнения первого порядка с разделяющимися
переменными и однородные.
Занятие 2. Линейные дифференциальные уравнения первого порядка.
Обзор методов интегрирования дифференциальных уравнений первого
порядка.
Занятие 3. Дифференциальные уравнения второго порядка, допускающие
понижение порядка f(х, у’, у’’) =0и f(у,у’,у”) = 0 и методы интегрирования.
Занятие 4. Комплексные числа в алгебраической форме и действия с ними.
Решение квадратных уравнений с отрицательным дискриминантом.
Однородные линейные дифференциальные уравнения с постоянными
коэффициентами. Фундаментальная система решений. Общее решение.
Задача Коши.
Занятие 5. Метод неопределённых коэффициентов для линейного
неоднородного дифференциального уравнения соспециальной правой
частью.правило наложения решений. Желательно использовать одинаковые
обозначения на кафедре.
Занятие 6. Метод неопределенных коэффициентов (продолжение). Метод
вариации произвольных постоянных.
Занятие 7. Подготовка к КР №2. «Дифференциальные уравнения» (выдача
пробного варианта КР №2).
Занятие 8. Контрольная работа КР №2 «Дифференциальные уравнения».
Занятие 9. Комбинаторика (основные формулы). Классическое определение
вероятности. Геометрическое определение вероятности.
Занятие 10. Теорема сложения вероятностей. Условная вероятность. Теорема
умножения вероятностей. Надежность систем, состоящих из последовательно
|
|
соединенных и параллельно соединенных элементов.
Занятие 11. Формула полной вероятности и формула Байеса.
Занятие 12. Испытания Бернулли. Формула Бернулли. Локальная и
интегральная формулы Муавра — Лапласа. Формула Пуассона. Простейший
поток событий.
Занятие 13. Дискретная случайная величина. Закон (ряд) распределения
дискретной случайной величины. Математическое ожидание и дисперсия.
Функция распределения.
Занятие 14. Непрерывная случайная величина. Функция распределения.
Плотность вероятности. Нахождение вероятности попадания случайной
величины в интервал. Нахождение функции распределения по известной
плотности. Математическое ожидание и дисперсия непрерывной случайной
величины.
Занятие 15. Нормальное распределение. Плотность вероятности.
Вероятностный смысл параметров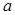 
и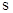 
. Вероятность попадания случайной
величины в произвольный интервал и в интервал, симметричный| относительно математического ожидания.
Занятие 16. Обзорное (типы экзаменационных задач).
Компьютерный практикум
Направление «Строительство» бакалавры 2020-2021 учебный год.
(0+1 ч КоП)
Занятие 1. Обзор методов вычисления неопределенных интегралов. Интегрирование
рациональных дробей. Интегрирование иррациональных функций с помощью степенной замены. Контрольные задания компьютерного практикума.
Занятие 2. Определенный интеграл по отрезку и его геометрические приложения. Контрольные задания компьютерного практикума.
Занятие 3. Компьютерное тестирование по теме «Неопределенный интеграл».
|
|
Занятие 4. Дифференциальные уравнения 1-го порядка. Задача Коши. Метод Эйлера. Контрольные задания компьютерного практикума.
Занятие 5. Компьютерное тестирование по теме «Обыкновенные дифференциальные уравнения».
Занятие 6. Обработка результатов эксперимента. Нахождение доверительных интервалов для математического ожидания и среднеквадратического отклонения нормально распределенной случайной величины. Контрольные задания компьютерного практикума.
Занятие 7. Статистическая оценка параметров распределения. Построение гистограммы по данной статистической совокупности. Контрольные задания компьютерного практикума.
Занятие 8. Компьютерное тестирование по теме «Теория вероятностей».