Так как выполнены неравенства
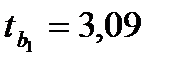> tкрит.(0,05;10)=2,23; 
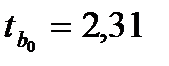> tкрит.(0,05;10)=2,23,
то следует вывод о том, что коэффициенты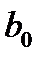 
и 
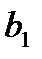значимы.
В ячейках Е15, Е16 получены границы доверительного интервала для генерального коэффициента регрессии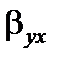 
с уровнем значимости 
:
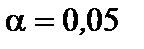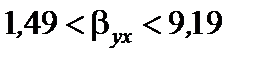
Проверка значимости уравнения регрессии (ячейки Е12, Е13):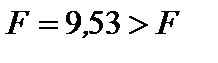 
крит.=4,96. Уравнение значимо с уровнем доверия 1-0,05=0,95=95%.
Построение доверительных границ для уравнения регрессии по формулам:
,
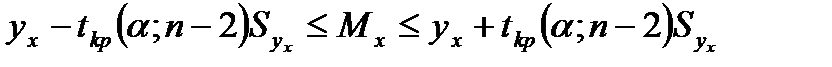где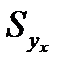 
- оценка групповой средней 
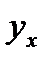, вычисляется по формуле:
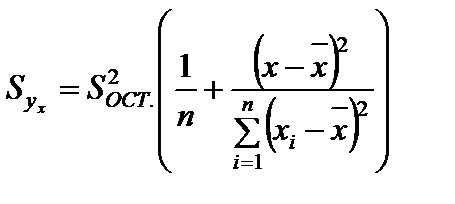
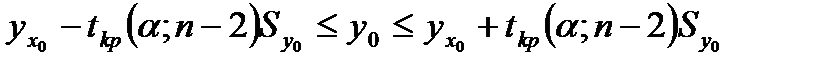
Пусть переменная х будет изменяться в диапазоне x=5; 5,3;…8. Таблица для вычислений доверительных границ строится в диапазоне F1:M12.
В диапазоне F1:M1 ввести обозначения x, Syx, Sy0, Yx, Y01, Yx1, Yx2, Y02.
В F2, F3 ввести числа 5 и 5,3, затем выделить ячейки F2:F3 и маркером заполнения протянуть вниз до F12.
В G2 ввести формулу
=E$6*КОРЕНЬ((1/12+(F2-E$4)^2/(11*ДИСП(A$2:A$13))))
и маркером заполнения протянуть ячейку G2 вниз до G12.
В ячейку Н2 ввести формулу
=E$6*КОРЕНЬ((1+1/12+(F2-E$4)^2/(11*ДИСП(A$2:A$13))))
и маркером заполнения протянуть ячейку Н2 вниз до Н12.
В диапазоне I2:M2 ввести формулы, указанные в таблице. Ввыделить диапазон I2:M2 и протянуть вниз до строки 12.
| I | J | K | L | M | |
| Yx | Y01 | Yx1 | Yx2 | Y02 | |
| =E$3+E$2*F2 | =I2-E$11*H2 | =I2-E$11*G2 | =I2+E$11*G2 | =I2+E$11*H2 |
В результате получится таблица для построения доверительных границ
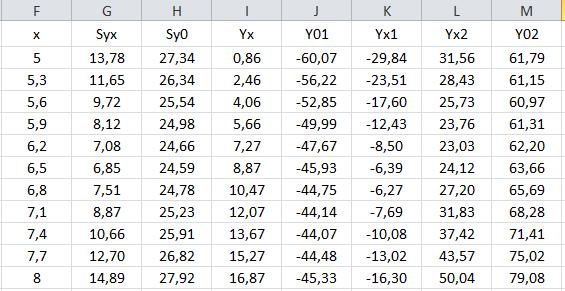
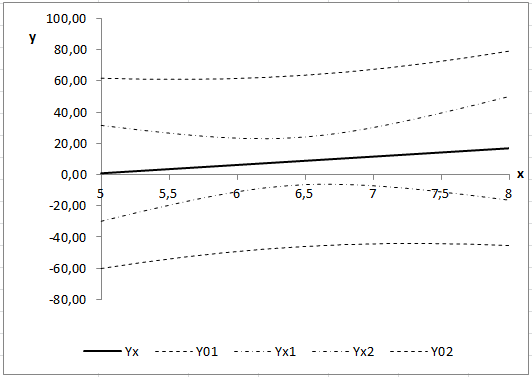
Чтобы построить график уравнения регрессии и графики доверительных границ, выделить диапазон F1:F12, затем, удерживая нажатой клавишу Ctrl, выделить диапазон I1:M12 и с помощью Мастера диаграмм построить диаграмму «Точечная».
На графике Yx1, Yx2 обозначают нижнюю и верхнюю доверительные границы для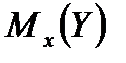 
, вычисляемые по формуле, а Y01 и Y02 обозначают нижнюю и верхнюю доверительные границы для индивидуальных значений 
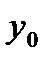, вычисляемые по формуле.
Решение с помощью Пакета анализа
Загрузить Пакет анализа и выбрать инструмент «Регрессия ».
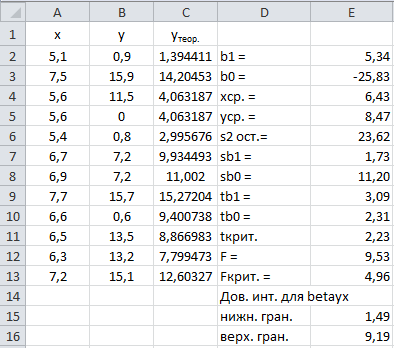
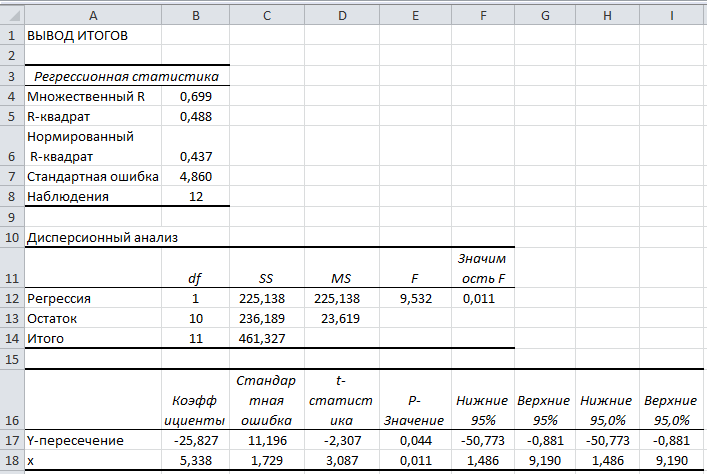
В диалоговом окне ввести следующие данные: Входной интервал Y: В1:В13, Входной интервал Х: А1:А13, поставить флажок в строках Метки и Уровень надёжности, в Параметрах выхода указать Новый рабочий лист и нажать кнопку ОК. Результаты представлены на рис.
Пример 3. Получить уравнение множественной регресии.
| X1 | 2,7 | 3,2 | 3,7 | 4,2 | 4,7 | 5,2 | 5,7 | 6,2 | 6,7 | 7,2 |
| X2 | 1,5 | 2,3 | 2,5 | 3,7 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,15 |
| Y |
Построить уравнение множественной линейной регрессии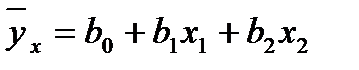 
. Проверить для уровня 
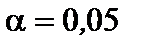значимость уравнения регрессии. Проверить значимость коэффициентов регрессии для уровня 
.
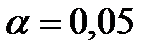Последовательность выполнения
Ввести данные в диапазоне A1:D15. В ячейках А1, В1, С1 и ввести метки переменных X1, X2, Y.
Вызвать Пакет анализа, инструмент «Регрессия » и в диалоговом окне ввести параметры: Входной интервал Y: $C$1:$C$11; Входной интервал Х: $А$1:$B$11; Выходной интервал: $А$15; отметить галочками все пункты в разделе Остатки. Нажать кнопку Ок. Результат состоит из четырёх таблиц и 2-х графиков.
Выводы:
Коэффициенты уравнения регрессии приведены в ячейках В17:В20, уравнение линейной регрессии имеет вид:
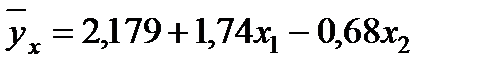
В разделе «Дисперсионный анализ» проводится оценка значимости уравнения регрессии. Значение в ячейке F26 практически равно нулю, т. е. это значение меньше уровня 0,05, что говорит о том, что уравнение регрессии значимо.
В ячейках D17:D19 приведены значения t-статистики, а в ячейках Е17:Е19 - значимости этих статистик. Так как значения в ячейках Е17 и Е18 близки к нулю (и меньше 0,05), то коэффициенты 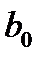и 
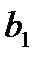значимы, а коэффициент 
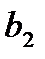незначим, так как Р-значение для него равно 0,234 (больше 0,05). Кроме того, доверительный интервал для этого коэффициента включает ноль (-1,912; 0,554). Необходимо исключить из уравнения регрессии слагаемое с х2 и повторить процедуру.
Пример 4. Построить по данным из таблицы уравнение нелинейной регрессии
| X | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 | 6,5 |
| Y | 1,2 | 1,8 | 1,9 | 2,1 | 2,2 | 2,9 | 3,7 | 4,3 | 4,5 | 4,9 | 5,1 | 5,2 |
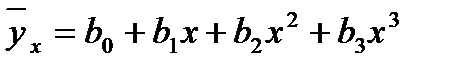; оценить значимость уравнения регрессии с уровнем 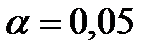; оценить значимость коэффициентов уравнения регрессии с уровнем .
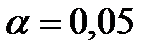Выполнение.
1. В ячейки A1:D1 ввести метки X, X2, X3 и Y.
2. Ввести значения переменной Х в диапазоне А2:А13.
3. В ячейку В2 ввести формулу: =A2^2 и протянуть маркером заполнения до вниз до В13.
4. В ячейку С2 ввести формулу: =A2^3 и протянуть маркером заполнения до вниз до С13.
5. Вызвать инструмент «Регрессия» Пакета анализа. В диалоговом окне указать:
Входной интервал Y: D1:D13, Входной интервал Х: А1:C13, поставить флажок в строках Метки и Уровень надёжности, в Параметрах выхода указать Новый рабочий лист и нажать кнопку ОК. Результаты представлены на рис.6.
1) Уравнение регрессии имеет вид: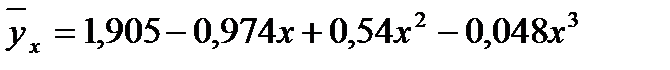 
. Уравнение регрессии значимо, так как значимость критерия Фишера (ячейка F12) <0,05. Коэффициент 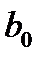незначим, так как Р-значение для него равно 0,157 (больше 0,05). Кроме того, доверительный интервал для этого коэффициента включает ноль
(-2,41; 0,463). Необходимо исключить из уравнения регрессии слагаемое с х (диапазон А1:А13) и повторить процедуру, поставив флажки в категории Остатки и Нормальная вероятность. Полученное уравнение регрессии имеет вид:
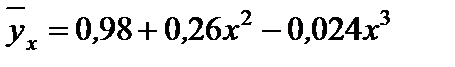
Уравнение регрессии значимо, все его коэффициенты значимы.
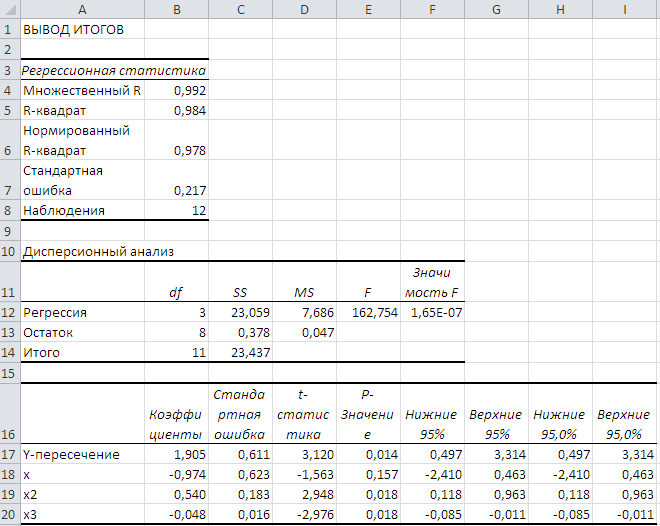
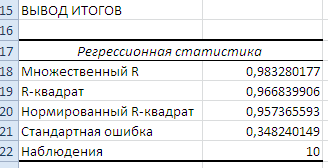
Рис.6.
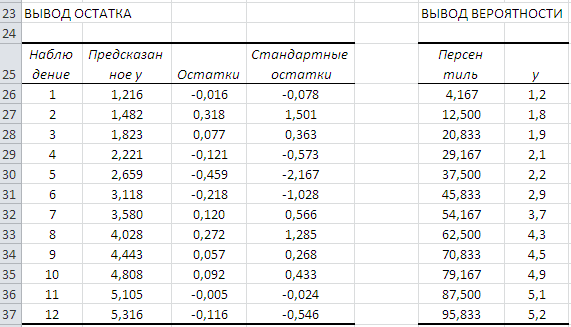
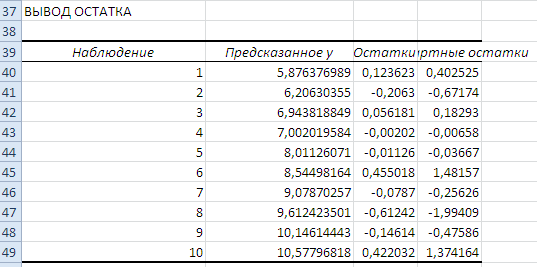
Будут выведены ещё две таблицы. В таблице ВЫВОД ОСТАТКА представлены: Наблюдение – порядковый номер в таблице исходных данных; Предсказанное у - значение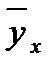 
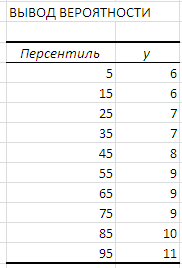
, рассчитанное по уравнению регрессии; Остатки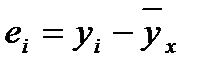 
; Стандартные остатки. В таблице ВЫВОД ВЕРОЯТНОСТИ представлены: Персентиль – рассчитывается для каждого значения 
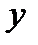как сумма предшествующего вычисленного персентиля и h=100% /наблюдения; начальное и конечное значения персентиля рассчитываются как 0+h/2 и
100-h/2 соответственно; 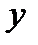- значения, расположенные в порядке возрастания.
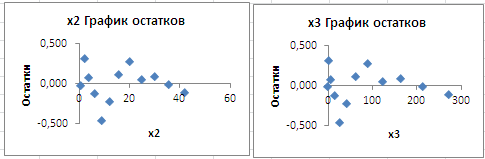
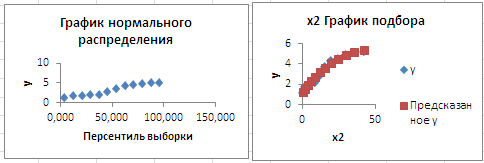
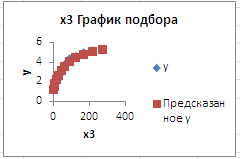
Кроме таблиц, Excel представляет графики: График нормального распределения строится по данным таблицы Вывод вероятности; Графики остатков для переменных х2 и х3; Графики подбора для переменных х2 и х3.
