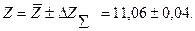Задача 1. Обработка результатов измерения величины Y.
Для величины y построить гистограмму плотности распределения результатов наблюдений, исключить промахи, рассчитать значение величины y и погрешность ее определения с учетом класса точности средств измерения, результат записать в виде
y = yср ± ΔyΣ
при заданной доверительной вероятности Р.
Дано: ряд равноточных измерений величины y (табл.1.1): доверительная вероятность Р = 0,9 класс точности СИ  .
.
Табл.1.1
| i | ||||||||
| y(i) | 14.32 | 16.06 | 21.61 | 14.4 | 15.55 | 15.14 | 14.64 | 14.88 |
| i | ||||||||
| y(i) | 15.71 | 14.4 | 14.73 | 14.88 | 15.52 | 16.11 | 15.66 | 14.59 |
Расставим измерения в порядке увеличения их значений (табл.1.2):
Табл.1.2
| i | ||||||||
| y(i) | 14.32 | 14.4 | 14.4 | 14.59 | 14.64 | 14.73 | 14.88 | 14.88 |
| i | ||||||||
| y(i) | 15.14 | 15.52 | 15.55 | 15.66 | 15.71 | 16.06 | 16.11 | 21.61 |
Определим нижнюю и верхнюю границы результатов и полученный числовой диапазон разобьем на 10 равных интервалов. Для каждого интервала рассчитываем число попаданий измерений, и представим результат на рис.1.1
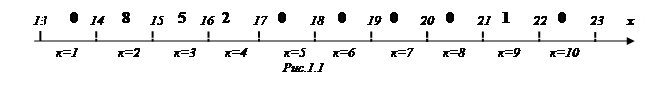
Определим относительную частоту попаданий результатов измерения в каждый из интервалов по формуле sк = nк/n, где: n=16 – общее число измерений, nк – число измерений, находящихся на к-том интервале:
s1 =0; s2 =0,5; s3 =0,3125; s4 =0,125; s5 = 0; s6 =0; s7 =0; s8 = 0; s9 =0,0625; s10 = 0
Очевидно, что сумма этих значений равна 1.  На рис.1.2 представлена гистограмма плотности распределения результатов наблюдений, где ширине прямоугольников соответствует величине участков разбиения, а высоте- величина sк. Из гистограммы следует, что в результатах измерений возможно наличие промаха при максимальном значении результата измерения. Проведем проверку данной гипотезы, воспользовавшись критерием Романовского.
На рис.1.2 представлена гистограмма плотности распределения результатов наблюдений, где ширине прямоугольников соответствует величине участков разбиения, а высоте- величина sк. Из гистограммы следует, что в результатах измерений возможно наличие промаха при максимальном значении результата измерения. Проведем проверку данной гипотезы, воспользовавшись критерием Романовского.
Рассчитаем среднее значение величины y
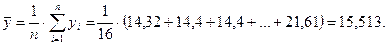
Определим СКО результатов наблюдений относительно среднего значения
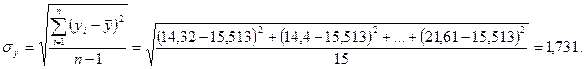
По табл.2.2 (1) при доверительной вероятности Р=0,9 и числе измерений n=16 выбираем коэффициент βt=2,49. Для всех значений yi определяем соотношение
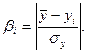
Значения βi для минимальных и максимальных значений результатов наблюдений приведены в табл.1.3. Остальные результаты не анализируем, т.к. промахи всегда находятся среди крайних значений.
| i | … | … | … | |||||||
| βi | 0.689 | 0.643 | 0.643 | … | … | … | 0.114 | 0.316 | 0.345 | 3.522 |
Из сравнения величин βt=2,49 и βi следует, что результат наблюдений y16=21,606 является промахом, т.к. β16=3,522 > βt=2,49, а остальные являются достоверными.
Сформируем ряд наблюдений величины y при исключенных промахах:
| i | ||||||||
| y(i) | 14.32 | 14.4 | 14.4 | 14.59 | 14.64 | 14.73 | 14.88 | 14.88 |
| i | |||||||
| y(i) | 15.14 | 15.52 | 15.55 | 15.66 | 15.71 | 16.06 | 16.11 |
Рассчитаем среднее значение величины х при числе измерений n = 15:

Определим опытное СКО среднего значения измеряемой величины

 По таблице коэффициентов Стьюдента для n=15 и Р=0,9 определяем значение
По таблице коэффициентов Стьюдента для n=15 и Р=0,9 определяем значение 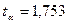 и рассчитываем величину максимально возможного отклонения измеренного значения величины х от его истинного значения без учета погрешности средств измерения
и рассчитываем величину максимально возможного отклонения измеренного значения величины х от его истинного значения без учета погрешности средств измерения
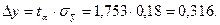
Рассчитаем максимальную погрешность используемых средств измерения с классом точности γ=0.01 и пределом измерений YN=100 по формуле
ΔСИ=(γ∙ YN)/100 =(0,01∙100)/100 = 0,01.
Суммарную погрешность измерений определим по соотношению
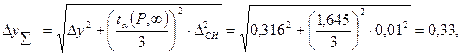
где tα =1,645 - значение коэффициента Стьюдента при Р=0,9 и бесконечном числе измерений n = ∞.
Ввиду того, что погрешность следует записывать с учетом не более двух значащих цифр, результат измерений представим в виде
y = 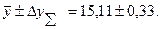
при доверительной вероятности Р=0,9.
Задача 2. Расчет значения величины Z.
По значениям величин х =  ± Δх = 14,23 ± 0,50 и у =
± Δх = 14,23 ± 0,50 и у = 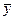 ± Δ у = 15,11 ± 0,33 рассчитать значение величины
± Δ у = 15,11 ± 0,33 рассчитать значение величины
Z = y/x+10.
Пример решения.
Среднее значение величины Z определим по формуле
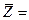 y/x+10=11,06.
y/x+10=11,06.
Величину максимальной погрешности параметра Z рассчитаем по соотношению

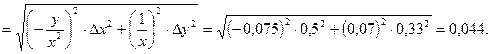 .
.
Результат определения величины Z запишем в виде: