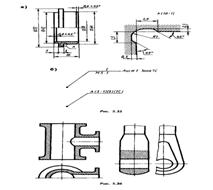
Рис. 159. Ступенчатый (а) и ломаный (б) разрезы
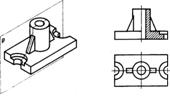
Рис. 160. Изображение ребер жесткости на разрезах
6) Ступенчатым называется сложный разрез, образованный двумя и более секущими параллельными плоскостями (рис. 159, а). Ступенчатые разрезы могут быть фронтальными, профильными и горизонтальными.
7)Местным разрезом называется разрез, служащий для выяснения устройства предмета лишь в отдельном ограниченном месте.
8)
| Соединение вида и разреза |
Соединение частей вида и разреза. Форма многих деталей не всегда может быть выявлена построением только видов, фронтального, горизонтального и профильного разрезов (рис. 164, а). Если форму детали отобразить только видами спереди и сверху, то не будет определено внутреннее устройство детали и глубина выемки. Если выполнить фронтальный разрез и вид сверху детали, то невозможно будет уяснить высоту элемента верхней части детали, называемого бобышкой. В этом случае допускается соединять части вида и разреза, границу между которыми проводят сплошной тонкой волнистой линией (рис. 164, б).
Бобышка представляет собой выступ на поверхности детали, предназначенный для крепления каких-либо других деталей. Как правило, бобышки имеют цилиндрические резьбовые отверстия или запрессованные резьбовые втулки. Бобышки могут быть прямоугольной или цилиндрической формы.
Соединение половин вида и разреза. На чертежах допускается соединять половину вида с половиной разреза в том случае, если оба изображения — симметричные. Изображения половин вида и разреза разделяются штрихпунктирной осевой линией. При соединении половин вида и разреза вид располагают слева или над осевой линией, а разрез — справа или под ней (рис. 165).
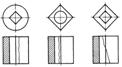
Есть исключение из рассмотренного правила. Если на чертеже с осью симметрии совпадает изображение ребра, то соединять половину вида с половиной разреза нельзя. В этом случае соединяют часть вида и часть разреза так, чтобы на изображении не исчезла линия контура (рис. 166).
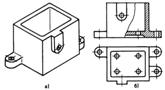 Рис. 164. Соединение частей вида и разреза
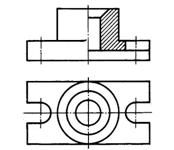Рис. 165. Соединение половин вида и разреза
|
9) Выносной элемент — изображение в более крупном масштабе какой-либо части предмета, содержащее подробности, не указанные на соответствующем изображении; он может отличаться от основного изображения по содержанию (например, изображение может быть видом, а выносной элемент — разрезом). Пример обозначения выносного элемента (рис. 5.35, а) — пояснение формы канавки для выхода шлифовального круга.
Исключены из условных надписей над изображениями (видами, разрезами, выносными элементами) слова «Лист», «Зона». Так, например, обозначение выносного элемента 1, выполненного в М 5:1 и расположенного на листе 2 в зоне 7С, теперь будет обозначаться так: А (5:1) (2) (7С) (рис. 5.35,6).
11)АКСОНОМЕТРИЯ — один из методов проецирования (получения проекции предмета на плоскости), с помощью которого наглядно изображают пространственные тела на плоскости бумаги. А. Делится на три вида: 1) изометрию (измерение по всем трем координатным осям одинаковое); 2) диметрию (измерение по двум координатным осям одинаковое, а по третьей — другое); 3) триметрию (измерение по всем трем осям различное). В каждом из этих видов проецирование м. б. прямоугольным и косоугольным.
- аксонометрические чертежи обратимы;
- аксонометрическая и вторичная проекции точки вполне определяют её положение в пространстве.
Аксонометрические проекции обратимы, если известна аксонометрия трех главных направлений измерений фигуры и коэффициенты искажения по этим направлениям.
Аксонометрические проекции фигуры являются её проекциями на плоскости произвольного положения при произвольно выбранном направлении проецирования.
В пространстве всегда возможно такое положение натуральной системы прямоугольных координат и такой размер натурального масштаба по осям, параллельной проекцией которых является данная аксонометрическая система.
Немецкий ученый Карл Польке (1810-1876) сформулировал основную теорему аксонометрии: три отрезка прямых произвольной длины, лежащих в одной плоскости и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на координатных осях от начала.
Виды аксонометрических проекций.
Аксонометрические проекции в зависимости от направления проецирования разделяют на:
косоугольные, когда направление проецирования не перпендикулярно плоскости аксонометрических проекций;
прямоугольные, когда направление проецирования перпендикулярно плоскости аксонометрических проекций.
В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:
изометрия — все три коэффициента искажения равны между собой (u = v = w);
диметрия — два коэффициента искажения равны между собой и отличаются от третьего (и не равно v = w или и= v не равно w);
триметрия — все три коэффициента искажения не равны между собой (u не равно v не равно w).
13) 1.1. Изометрическая проекция
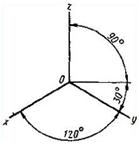
1.1.2. Коэффициент искажения по осям х, у, z равен 0,82. Изометрическую проекцию для упрощения, как правило, выполняют без искажения по осям х, у,z, т. е. приняв коэффициент искажения равным 1.
1.2. Диметрическая проекция
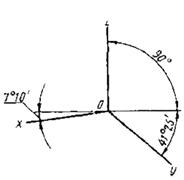
1.2.2. Коэффициент искажения по оси у равен 0,47, а по осям х и z- 0,94. Диметрическую проекцию, как правило, выполняют без искажения по осям х и z и с коэффициентом искажения 0,5 по оси у.
2.1. Фронтальная изометрическая проекция
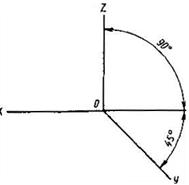
Допускается применять фронтальные изометрические проекции с углом наклона оси у 30 и 60.2.1.2. Фронтальную изометрическую проекцию выполняют без искажения по осям х, у, z.
Горизонтальная изометрическая проекция
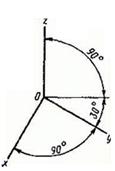
Допускается применять горизонтальные изометрические проекции с углом наклона оси у 45 и 60, сохраняя угол между осями х и у 90.2.2.2. Горизонтальную изометрическую проекцию выполняют без искажения по осям х, у и z.
2.3. Фронтальная диметрическая проекция
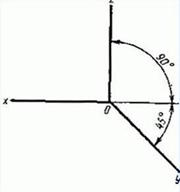
Допускается применять фронтальные диметрические проекции с углом наклона оси у 30 и 60. Коэффициент искажения по оси у равен 0,5, а по осям х и z-1.
14) 1.1. Изометрическая проекция
1.1.3. Окружности, лежащие в плоскостях, параллельных плоскостям проекций проецируются на аксонометрическую плоскость проекций в эллипсы. Если изометрическую проекцию выполняют без искажения по осям х, у, z, то большая ось эллипсов 1, 2,3 равна 1,22, а малая ось-0,71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям х, у, z, то большая ось эллипсов 1, 2,3 равна диаметру окружности, а малая ось-0,58 диаметра окружности.
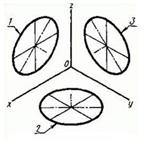
1.2. Диметрическая проекция
1.2.3. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы. Если диметрическую проекцию выполняют без искажения по осям х и z, то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1- 0,95, эллипсов 2 и 3-0,35 диаметра окружности. Если диметрическую проекцию выполняют с искажением по осям х и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1- 0,9, эллипсов 2 и 3- 0,33 диаметра окружности.
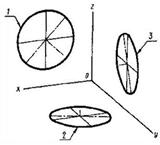
2.1. Фронтальная изометрическая проекция
2.1.3. Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций,-в эллипсы. Большая ось эллипсов 2 и 3 равна 1,3, а малая ось-0,54 диаметра окружности.
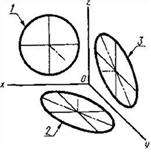
2.2. Горизонтальная изометрическая проекция
2.2.3. Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций-в эллипсы. Большая ось эллипса 1 равна 1,37, а малая ось-0,37 диаметра окружности. Большая ось эллипса 3 равна 1,22, а малая ось-0,71 диаметра окружности.
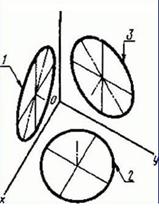
2.3. Фронтальная диметрическая проекция
2.3.2. Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций,-в эллипсы. Большая ось эллипсов 2 и 3 равна 1,07, а малая ось-0,33 диаметра окружности.
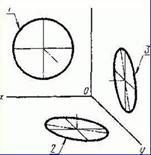
15)Эллипс — плоская кривая, являющаяся геометрическим местом точек, сумма расстояний от каждой из которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.
Эллипсом называется геометрическое место точек М плоскости, сумма расстояний которых от двух данных точек F1 и F2 есть величина постоянная и равная отрезку АВ (рис. 37, а). Точки F1 и F2 называются фокусами эллипса; отрезок АВ — большой осью; отрезок CD, перпендикулярный к АВ, — малой осью; точка О — центром эллипса. Большую ось выражают через 2а, малую — через 2 b, отрезок F1 F2 (расстояние между фокусами) — через 2с.
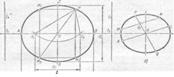
Прямые, соединяющие произвольную точку М эллипса с фокусами, называются радиус-векторами данной точки. Согласно определению, сумма расстояний любой точки эллипса до его фокусов, т. е. сумма радиус-векторов, равна длине большой оси:
MF1 + MF2 = АВ = 2а.
Из этого следует, что CF1+ CF2= 2а, но CF1= CF2, следовательно, CF1 = а. Поэтому для нахождения фокусов эллипса, если даны его оси, необходимо из конца малой оси, например точки С, провести дугу радиусом, равным а (половине большой оси), которая пересечет большую ось в точках F1 и F2 — фокусах эллипса.
Между величинами а, b и с существует следующая зависимость:
а2 = b2 + с2.
Уравнение эллипса выражается формулой
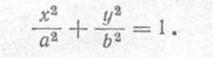
Отношение величины малой оси эллипса к большой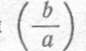 
называется коэффициентом сжатия эллипса, а отношение фокусного расстояния к большой оси — эксцентриситетом эллипс, а отношения фокусного расстояния к большой оси - эксцентриситетом эллипса 
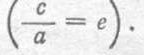Директрисами называются прямые l1 и l2 (см. рис. 37, а), параллельные малой оси эллипса и отстоящие от его центра на расстоянии
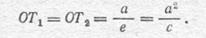
Каждой точке эллипса соответствуют две точки, расположенные симметрично относительно большой и малой осей, и одна точка, расположенная симметрично относительно центра эллипса. На рис. 37, а точки, симметричные точке М, обозначены М1, М2, М3.
Прямая, проходящая через центр эллипса, называется его диаметром. Большая и малая оси называются главными диаметрами эллипса. Два диаметра эллипса называются сопряженными, если каждый из них делит пополам хорды, параллельные другому диаметру. Для построения диаметра PQ, сопряженного диаметру KL (рис. 37, б), проводят хорду MN, параллельную диаметру KL, и делят ее пополам. Соединив точки О и 01, получают диаметр PQ, сопряженный данному.
16) Hа чертеже сечения выделяют штриховкой. Вид ее зависит от гpафического обозначения матеpиала детали и должен соответствовать ГОСТ 2.306 - 68*
Металлы и твеpдые сплавы в сечениях обозначают наклонными паpаллельными линиями штpиховки, пpоведенными под углом 45 гpадусов к линии контуpа изобpажения или к его оси, или к линиям pамки чеpтежа Если линии штpиховки, пpоведенные к линиям pамки чеpтежа под углом 45 гpадусов, совпадают по напpавлению с линиями контуpа или осевыми линиями, то вместо угла 45 гpадусов следует бpать угол 30 или 60 гpадусов
Линии штpиховки должны наноситься с наклоном влево или впpаво, но как пpавило, в одну и ту же стоpону на всех сечениях, относящихся к одной и той же детали, независимо от количества листов, на котоpых эти сечения pасположены.
Pасстояние между паpаллельными пpямыми линиями штpиховки (частота) должно быть, как пpавило, одинаковым для всех выполняемых в одном и том же масштабе сечений данной детали. Указанное pасстояние должно быть от 1 до 10 мм в зависимости от площади штpиховки и необходимости pазнообpазить штpиховку смежных сечений.
Узкие и длинные площади сечений (напpимеp, штампованных деталей), шиpина котоpых на чеpтеже от 2 до 4 мм, pекомендуется штpиховать полностью только на концах и у контуpов отверстий, а остальную площадь сечения - небольшими участками в нескольких местах Узкие площади сечений, ширина котоpых на чеpтеже менее 2 мм, допускается показывать зачеpненными с оставлением просветов между смежными сечениями не менее 0,8 мм
Для смежных сечений двух деталей следует бpать наклон линий штpиховки для одного сечения впpаво, для дpугого - влево (встpечная штpиховка).
Пpи штpиховке "в клетку" для смежных сечений двух деталей pасстояние между линиями штpиховки в каждом сечении должно быть pазным.
В смежных сечениях со штpиховкой одинакового наклона и напpавления следует изменять pасстояние между линиями штpиховки или сдвигать эти линии в одном сечении по отношению к другому, не изменяя угла их наклона.