Силы инерции, действующие на тело во вращающейся системе отсчёта

Движение в неинерциальных системах отсчета

 

Неинерциальность заключается в том, что K’ движется поступательно (v₀ 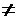const) относительно К и вращается с угловой скоростью 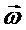относительно точки O’.

 

Абсолютное движение – т. М относительно К.

Относительное движение – т. М относительно К’.

Переносное движение – K’ относительно К.

 

Абсолютная скорость:

.

 

 

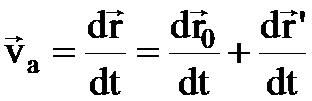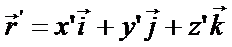
К’ движется относительно К неравномерно поступательно, да еще и вращается, поэтому со временем изменяются как x’y’z’ так и направления векторов .

 

 

 

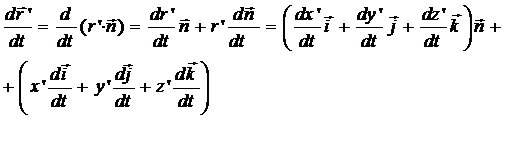
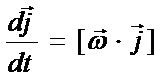
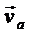- абсолютная скорость т. М – K;

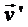- относительная скорость т. M – K’;

Переносная скорость:

 

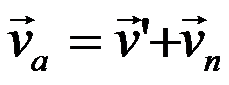
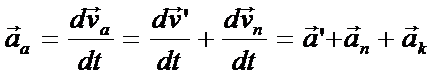
Абсолютное ускорение материальной точки равно сумме относительного, переносного и кориолисова:

 

,

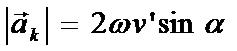
Частные случаи:

1. K’ – движется только поступательно ,

 

, ,

, .

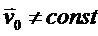
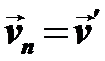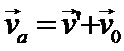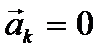2. K’ – тоже инерциальна ,

 

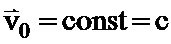
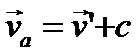
- ускорение и силы в обеих системах одинаковы.

 

Силы инерции

 

2-ой закон Ньютона:

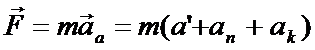
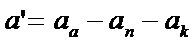
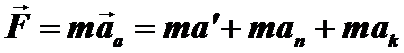
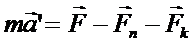
- переносная сила инерции.

Для общего случая движения ,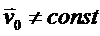

 

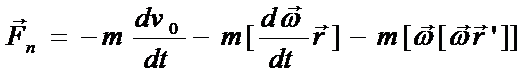
1. 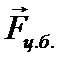- центробежная сила инерции:

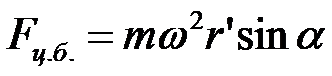
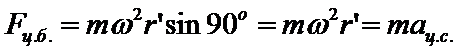
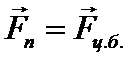, если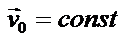

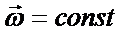
2. 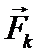- гироскопическая или кориолисова сила.

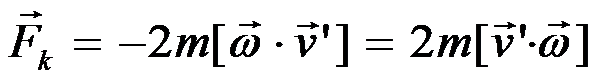
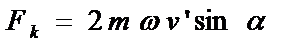
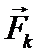
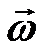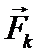
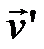
1) , 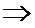гироскопическая сила.

2) 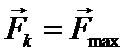, если , .

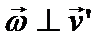3) , , .

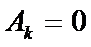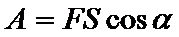Неинерциальные системы отсчёта. Силы инерции

 

Системы отсчёта, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными.

Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчёта:

 

F + F_ин

Так как F=ma (a – ускорение тела в инерциальной системе отсчёта), то

F_ин + ma

 

Силы инерции при ускоренном поступательном движении системы отсчёта.

Пусть на тележке к штативу на нити подвешен шарик массой m. Пока тележка покоится или движется равномерно и прямолинейно, нить, удерживающая шарик, занимает вертикальное положение и сила тяжести P уравновешивается силой реакции нити T.

F – результирующая сила и равна F = P + T

Результирующая сила F направлена в сторону ускорения тележки a₀

F=mg tgma₀

tg a₀ /g

F_ин = -ma₀

Силы инерции, действующие на тело во вращающейся системе отсчёта

Пусть диск равномерно вращается с угловой скоростью (=const) вокруг вертикальной оси, проходящей через его центр. На диске, на разных расстояниях от оси вращения, установлены маятники (на нитях подвешены шарики массой m). При вращении маятников вместе с диском шарики отклоняются от вертикали на некоторый угол.

В инерциальной системе отсчёта шарик равномерно вращается по окружности радиусом R. На него действует сила, равная F=m²R и направленная перпендикулярно оси вращения диска.

F – равнодействующая сила и равна F = P+ T

F=mg tg m²R

tg²R/g

F_ц - центробежная сила инерции, направлена по горизонтали от оси вращения диска и равна F_ц = -m²R

 

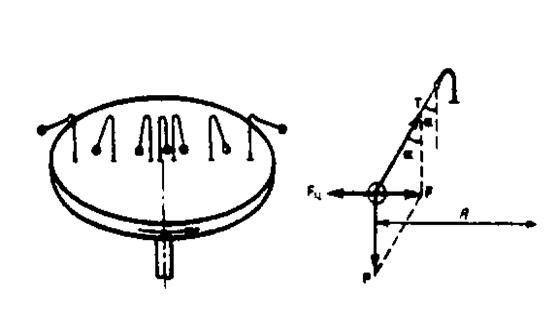
Центробежная сила инерции действует во вращающихся системах отсчёта на все тела, удалённые от оси вращения на конечное расстояние, независимо от того, покоится ли они в этой системе или движется относительно её с какой-то скоростью.

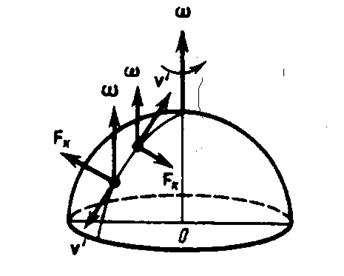
3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчёта.

Пусть шарик массой m движется с постоянной скоростью вдоль радиуса равномерно вращающегося диска ( =const,  = const, ). Если диск не вращается, то шарик, направленный вдоль радиуса, движется по радиальной прямой и попадает в точку А, если же диск привести во вращение в направлении, указанном стрелкой, то шарик катится по кривой ОВ, причём его скорость относительно диска изменяет своё направление. Это возможно лишь тогда, если на шарик действует сила, перпендикулярная скорости .

Шарик движется без трения равномерно и прямолинейно со скоростью . При отклонении шарика стержень действует на него с некоторой силой F. Относительно диска (вращающейся системы отсчёта) шарик движется равномерно и прямолинейно, что можно объяснить тем, что сила F уравновешивается приложенной к шарику силой инерции F_к, перпендикулярной скорости . Эта сила называется кориолисовой силой инерции.

F_к = .

 

 

Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчёта, например, относительно Земли. Если тело движется в северном полушарии на север, то действующая на него сила Кориолиса, будет направлена вправо по отношению к направлению движения, т.е. тело несколько отклоняется на восток и наоборот.

 

– основной закон динамики в неинерциальных системах отсчета.

Сила тяжести

Рис 6.2, стр. 80

 

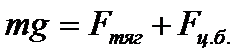
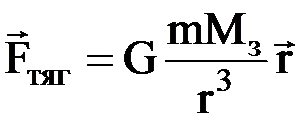
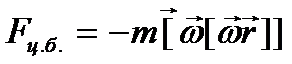
Полюсы: , ,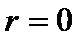

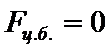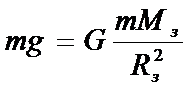
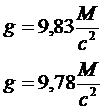
Экватор: пропорционально 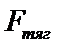- 35%,