Лабораторная работа №3
Тема: Метод Ньютона
Руководитель Рогов В.П.
Исполнитель студент гр. С-110 Щелков Е.И.
Работу выполнил:
Работу защитил:
Теоретическое введение: Метод Ньютона
Вывод итерационной формулы
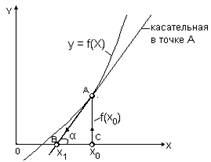Рис. 1.3
|
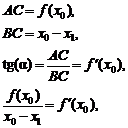
из последнего соотношения получаем
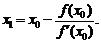
Алгоритм метода Ньютона:
1) принимаем и вводим в ЭВМ начальное значение x и допустимую погрешность вычисления корня ε;
2) присваиваем величине x 0 значение x;
3) вычисляем новое значение
;
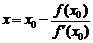4) анализируем условие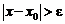 
. если это условие выполняется, то переходим к пункту 2, т. е. продолжаем поиск корня; иначе выводим в качестве результата величину x.
Данный метод предполагает наличие у функции f (x) не только свойства непрерывности, но еще и дифференцируемости. Однако метод Ньютона можно применять и для недифференцируемых функций. В этом случае можно воспользоваться разностным аналогом производной
.
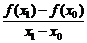Такой подход иллюстрируется на рис. 1.4.
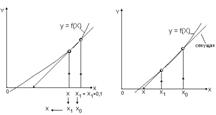
а б
Рис. 1.4: а – начало; б – продолжение
Алгоритм метода Ньютона с разностной производной:
1) вводим в ЭВМ x и ε;
2) формируем дополнительную точку x 1 = x + 0,1;
3) формируем две точки для проведения секущей
x 0 = x 1,
x 1 = x;
4) вычисляем новое значение
;
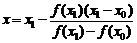5) анализируем условие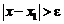 
. если это условие выполняется, то переходим к пункту 3, т. е. продолжаем поиск корня; иначе выводим в качестве результата величину x.
Метод Ньютона нельзя использовать для функций, у которых в окрестности корня производная близка к нулю.
Упрощенный метод Ньютона
Если производная функции f ′(x) в процессе поиска корня изменяется мало, то можно еë вычислить один раз в начальной точке x 0.
|
|
Тогда итерационная формула поиска запишется в виде:
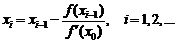
Данный подход иллюстрируется на рис. 1.5.
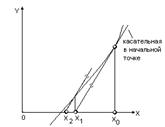
Рис. 1.5
Метод Ньютона сходится быстро, однако для обеспечения его сходимости нужно определённым образом задавать начальную точку x 0.
Условие сходимости (необходимое и достаточное) (см. рис. 1.6):
.
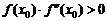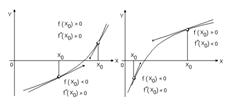
а б
Рис. 1.6
Решение систем нелинейных уравнений
методом Ньютона-Рафсона
Дана система нелинейных уравнений с n неизвестными:
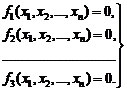(1.14)
Разложим в ряд Тейлора каждую функцию fi (x 1, x 2,…, xn) в начальной точке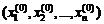 
, обозначив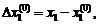 
,
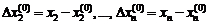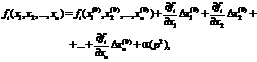(1.15)
где α(p 2) – бесконечно малое по сравнению с
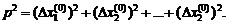
Учитывая в разложении (1.15) только линейные члены относительно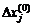 
и заметив, что из (1.14) имеем fi (x 1, x 2,…, xn) = 0, получаем систему линейных уравнений относительно приращений :
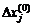В развёрнутой матричной форме полученная система уравнений будет иметь следующий вид:
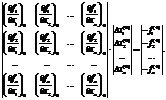(1.16)
Введя векторные обозначения, можем записать систему (1.16) в виде
JDx = – F,
где J – квадратная матрица Якоби;
Dx – вектор приращений Δ xj;
F – вектор правых частей системы.
Систему линейных уравнений (1.16) можно решать любым известным методом, например, методом Гаусса.
Алгоритм решения:
1) ввод исходных данных:
ε – допустимая абсолютная погрешность в вычислении решения;
n – количество уравнений для вычисления неизвестных xj;
m – максимальное количество итераций;
X 0 – вектор начальных приближений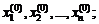 
h – приращение xj для вычисления частных производных в разностной форме;
2) вычисление элементов вектора F в начальной (текущей) точке, определяемой вектором X 0;
|
|
3) вычисление элементов матрицы J – частных производных:
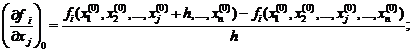
4) решение линейной системы (1.16) – вычисление элементов вектора Dx;
5) корректировка начального (текущего) приближения решения – вычисление вектора
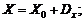
6) проверка погрешности решения по условию
При выполнении этого условия вектор X выводится в качестве решения системы, а иначе переформируется вектор начальных приближений (X 0 = X) и осуществляется переход к пункту 2 на выполнение очередной итерации. Количество итераций ограничивается числом m. При его превышении выдается сообщение о необходимости выбора лучшего начального приближения.
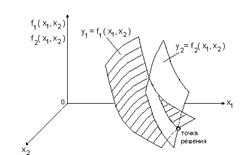
Для решения системы из двух нелинейных уравнений возможна геометрическая интерпретация.
Каждой из нелинейных функций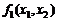 
и 
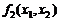, стоящих в левой части первого и второго уравнений, соответствует в пространстве некоторая изогнутая поверхность y 1 и y 2. В точке начального приближения 
будем иметь значения функций:
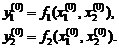
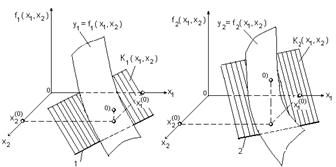
Разложим выражение каждой функции в окрестности точки начального приближения в ряд Тейлора, тогда получим выражения:
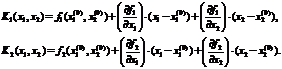
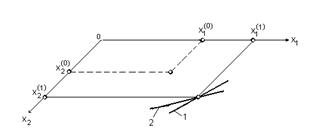
Эти выражения описывают касательные плоскости к поверхностям y 1 и y 2 в соответствующих точках с координатами . Эти плоскости имеют следы пересечения с плоскостью x 1 Ox 2 в виде прямых линий. В свою очередь пересечение этих прямых даёт точку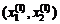 
очередного приближения к решению системы (рис. 1.7).
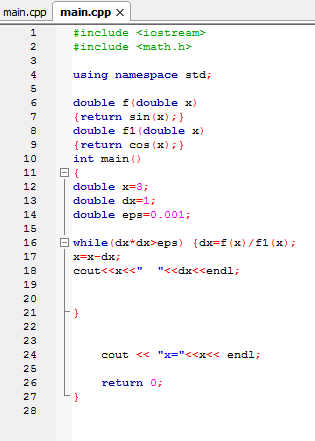
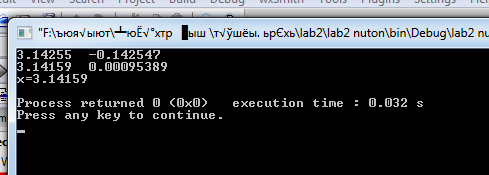
Практическая часть:
