Вектор скорости направлен перпендикулярно расстоянию от точки до оси вращения
Вывод:
Если мы знаем угловую скорость тела в данный момент времени, тогда для того чтобы найти скорость любой точки достаточно знать ее расстояние до оси. Умножив модуль угловой скорости на это расстояние, мы получим скорость любой точки данного тела.
Определение ускорения.
Ускорение характеризует изменение скорости по времени. А скорость величина векторная. Она характеризуется модулем и направлением.
Поэтому одна составляющая ускорения учитывает, как меняется модуль скорости Wτ = 
, а вторая величина Wn = 
учитывает изменение скорости по направлению.
Вследствие, искривления траектории скорость 
меняет модуль и направление. Поэтому вектор ускорения можно записать следующим образом:
= τ + n
где
Wτ = ; Wn =
Для выбранной точки М h величина постоянная. Подставляя формулу (1) получаем:
Wτ = h 
|
(3)
Теперь нормальное ускорение: вместо скорости подставляем его значение 
= h ω, а радиус кривизны окружности равен h
Получаем:
Wn = 
= hω2
|
(4)
Введем новые обозначения, которые используются только для точек вращающегося тела.
Принимаем обозначения
Wω = h ε (3»)
Wω – центростремительное ускорение точки М, вектор данного ускорения всегда направлен по радиусу окружности к центру.
Wε 
МС
Wε = h ω2 (4»)
Wε - вращательное ускорение точки М, вектор данного ускорения всегда направлен по касательной к траектории в строну 
.
Wε 
МС
Т.к Wε Wω, то модуль полного ускорения
|
= h 
(5)
Необходимо указать величину, которая будет характеризовать направление этого вектора. Для этого изобразим следующие картинки.
|
|
Изображаем траекторию движения точки М и вектор скорости.
Движение может быть ускорено или замедленно.
 |
Как бы не вращалось тело, центростремительное ускорение будет направлено в сторону вогнутости траектории, а вращательная составляющая направлена в сторону углового ускорения.
Полное ускорение определяется по правилу параллелограмма.
Теперь мы можем ввести угол α отклонения полного ускорения от радиуса.
Направление полного ускорения характеризует тангенс угла 
.
Из прямоугольного треугольника:
|
= 
(6)
Выводы:
Вращательная скорость, вращательное и центростремительное ускорение пропорциональны расстоянию от оси вращения.
2. Угол α отклонения полного ускорения от радиуса описываемой окружности одинаков для всех точек твердого тела в данный момент времени.(не зависит от положения точки М в теле)
Полное ускорение образует один и тот же угол с радиусами описываемых ими окружностями.
2. Векторные формулы для определения скорости и ускорения любой точки вращающегося тела.
Угловая скорость и угловое ускорение, как векторы.
Данные формулы угловой скорости и ускорения
ω = 
ε = 
= 
определяют угловую скорость и угловое ускорение, как алгебраические величины.
Знак угловой скорости показывает, в какую сторону вращается тело.
Целесообразно во многих случаях ввести понятия вектора угловой скорости и углового ускорения.
Будем рассматривать угловую скорость как вектор.
|
|
Введем обозначение:
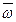- вектор угловой скорости.
Т.к. вводимая нами величина векторная, то необходимо указать чему будет равен модуль и как этот вектор направлен.
Договоримся под модулем этого вектора понимать абсолютное значение:
| | = | 
| = | 
|
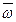Будем направлять по оси OZ.
Изобразим картинку
Ось Z характеризуется единичным ортом k.
Рассматриваем правую тройку векторов.
Мы договорились положительное направление считать такое, при котором поворот виден против часовой стрелки, если смотреть с конца вектора OZ.
Вектор угловой скорости 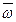будем направлять туда, куда направлен винт с правой нарезкой (правило Буравчика)
Изобразим орт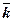 
в точке О.
Тогда мы сможем записать:
= 
= 
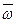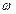
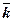- является вектором скользящим