|
(7)
|
(7»)

Будем считать вектора 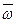 и
и  - векторами скользящими, будем прикладывать их в точке О начале координат.
- векторами скользящими, будем прикладывать их в точке О начале координат.
Введенные нами вектора 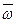 и
и  обладают следующими достоинствами:
обладают следующими достоинствами:
1. Вектор угловой скорости 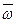 позволяет определить не только скорость и направление вращения (т.к. мы договорились направлять его по оси) но и положение оси вращения.
позволяет определить не только скорость и направление вращения (т.к. мы договорились направлять его по оси) но и положение оси вращения.
2. 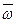 и
и  позволяют получить векторные формулы скорости и ускорения любой точки вращающегося тела по величине и направлению.
позволяют получить векторные формулы скорости и ускорения любой точки вращающегося тела по величине и направлению.
3. 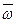 и
и  полезны при изучении последующих видов движения твердого тела.
полезны при изучении последующих видов движения твердого тела.
Сейчас с помощью этих векторов мы сумеем написать вектор скорости точки и ускорения.
Векторная формула Эйлера для определения скорости точки вращающегося тела.
Изобразим ось вращения OZ, точку М тела, совершающего вращательное движение, находящуюся на расстоянии h от оси вращения.
Радиус вектор  этой точки относительно неподвижного полюса О (начала координат).
этой точки относительно неподвижного полюса О (начала координат).
Изображаем вектор угловой скорости 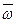 , и затем вектор скорости
, и затем вектор скорости  .
.
Угол между 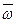 и
и  обозначим β.
обозначим β.
Утверждаем, что


Чтобы убедиться будем сравнивать два вектора между собой, слева будем писать все, что нам известно о векторе скорости этой точки  , а справа составим векторное произведение
, а справа составим векторное произведение 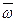

 .
.
Если мы убедимся, что эти два вектора имеют одинаковые модули, одинаково направленные, то они будут равны друг другу.
Т.о. мы получим векторную формулу для скорости любой точки М.

|
  
|
Модуль данного вектора, как известно равен
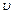 = h | = h | 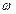 |
он будет направлен в сторону вращения |
он будет направлен в сторону вращения
 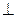 площадке содержащей( площадке содержащей(  ) )
|
|    | = | | = |  | | | |  | sin ( | sin (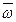  )
или
| )
или
|    | = | | = | 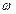 | r sin β = h | | r sin β = h | 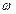 |
Он будет направлен |
Он будет направлен
   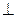 площадке содержащей
( площадке содержащей
(  ) )
|
По определению векторного произведения 

 - это третий вектор расположенный перпендикулярно площадке содержащей эти два вектора. В сторону откуда поворот от вектора
- это третий вектор расположенный перпендикулярно площадке содержащей эти два вектора. В сторону откуда поворот от вектора  к вектору
к вектору  - виден против часовой стрелки.
- виден против часовой стрелки.
В нашем случае он нарпавлен также как вектор  .
.
Заключение т.к. эти вектора равны по модулю и по направлению, тл они одинаковы.
 =
= 

 (8)
(8)
Формула (8) называется векторной формулой Эйлера.
Определение.
Вектор скорости любой точки вращающегося тела направлен перпендикулярно радиусу вращения или расстоянию от точки до оси вращения, в сторону вращения тела
Векторные формулы для определения ускорения любой точки вращающегося тела.
Как известно
 =
= 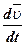
Но если вспомнить формулу Эйлера, то можно записать:
 =
= 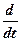 (
(

 )
)
В нашем случае обе эти величины переменные, поэтому получаем следующую формулу:
 =
= 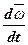

 +
+ 


Теперь вспоминаем:
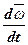 =
= 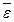 ,
,  =
= 
или
 =
= 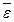

 +
+ 
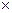 (
(

 ) (9)
) (9)
Где первое слагаемое:
 =
= 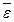

 - это вектор вращательной составляющей ускорения точки М.
- это вектор вращательной составляющей ускорения точки М.
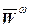 =
= 
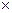 (
(
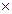
 ) – это векторцентростремительной составляющей ускорения точки М.
) – это векторцентростремительной составляющей ускорения точки М.
По определению векторного произведения двух векторов вектор 

 направлен по радиусу окружности описываемой точкой М, к центру окружности., т.е. как вектор
направлен по радиусу окружности описываемой точкой М, к центру окружности., т.е. как вектор 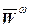

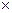
 ↓↓
↓↓ 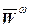
далее по модулю
| 
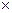
 | = |
| = |  | |
| |  | sin 90 = | ω| υ
| sin 90 = | ω| υ
т.к.
υ =| ω| h, то
| 
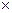
 | = ω2h,
| = ω2h,
т.о
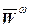 =
= 
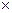
 =
= 
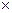 (
(
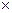
 )
)
Последнюю формулу можно записать по-другому
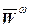 = - ω2
= - ω2 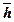
где 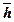 - радиус вектор точки М относительно центра окружности, описанной этой точкой.
- радиус вектор точки М относительно центра окружности, описанной этой точкой.
 =
=  +
+ 
 =
= 
 =
= 
 =
= 