II. Вычисление оценок математического ожидания и дисперсии

ПРИМЕР ВЫПОЛНЕНИЯ ТИПОВОГО РАСЧЁТА

Измерен характерный размер 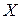деталей, обрабатываемых на некотором станке. Замерено 60 деталей. Данные замеров приведены в таблице.

№ детали	Размер	№ детали	Размер	№ детали	Размер
	72,58		72,50		72,30
	72,35		72,69		72,28
	72,33		72,54		72,51
	72,54		72,48		72,37
	72,24		72,36		72,14
	72,42		72,50		72,42
	72,58		72,43		72,36
	72,47		72,46		72,28
	72,54		72,56		72,20
	72,35		72,48		72,48
	72,38		72,43		72,60
	72,70		72,56		72,64
	72,47		72,34		72,73
	72,49		72,38		72,43
	72,24		72,56		72,28
	72,28		72,32		72,64
	72,47		72,41		72,72
	72,95		72,14		72,35
	72,18		72,29		72,60
	72,66		72,31		72,46

Обработаем результаты этого опыта по следующему плану:

I. Построим статистическое распределение выборки.

II. Вычислим оценки математического ожидания и дисперсии.

III. Построим гистограмму относительных частот, установив статистический (эмпирический) закон распределения и запишем его функцию плотности. С помощью критерия 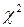(Пирсона) проверим гипотезу о согласии эмпирического закона распределения случайной величины 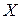с нормальным законом распределения (законом Гаусса).

IV. Построим кривую нормального распределения, приняв за параметры кривой найденные оценки математического ожидания и дисперсии (желательно на одном чертеже с гистограммой).

V. Найдём доверительный интервал для оценки математического ожидания и дисперсии.

I. Построение статистического распределения выборки

1. Данную выборку преобразуем в вариационный (интервальный) ряд. Строим его так: диапазон изменения случайной величины 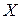в выборке объема 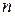делим на 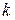интервалов. Число интервалов определяем по формуле 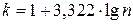с округлением до ближайшего целого. В нашем примере .

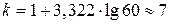Ширину каждого интервала берем одинаковой и равной .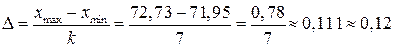

Границы интервалов вычисляем по формуле .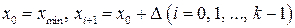

3. По протоколу выборки подсчитываем количество элементов n_i, попавших в i -й интервал (частота интервала). Если элемент совпадает с границей интервала, то он относится к предыдущему интервалу.

4. Вычисляем относительные частоты интервалов .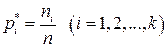

Полученные данные вносим в таблицу 1.

II. Вычисление оценок математического ожидания и дисперсии

Известно, что оценки математического ожидания и дисперсии вычисляются по формулам 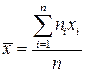, , 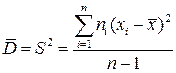где – частота варианты 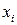, 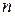– объём выборки. Если объем выработки велик, то вычисление точечных оценок математического ожидания 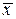и дисперсии 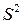по приведённым формулам громоздко. Для сокращения вычислений элементам выборки, попавшим в i- й интервал, припишем значения равные серединам интервалов .

Для упрощения дальнейших выкладок варианты 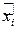заменяем новыми 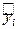по формул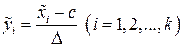е , где 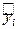называется условной вариантой, с – ложным нулем (новым началом отсчета).

Замечание 1. Если число интервалов нечетное, то в качестве ложного нуля берем середину среднего интервала, если четное, то середину того интервала, у которого больше частота.

Замечание 2. Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю.

Значения 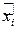и 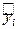вносим в таблицу 1.

Для вычисления оценки 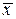подсчитаем произведения 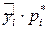и 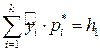и внесем в таблицу 2. В нашем примере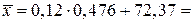 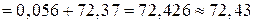– оценка математического ожидания.

Для вычисления оценки 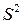подсчитаем произведения 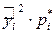и и внесем в таблицу 2. В нашем примере , .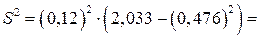

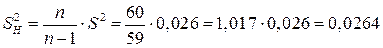Далее вычисляем оценку среднего квадратического отклонения .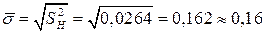

Для сравнения подсчитаем 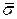по «правилу 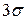». Так как для случайной величины, имеющей нормальное распределение, почти все рассеивания укладывается на участке 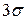, то с помощью этого правила можно ориентировочно определить оценку среднего квадратического отклонения случайной величины. Берем максимальное практически возможное отклонение от среднего значения и делим его на три.

В нашем примере , , , , , .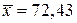

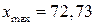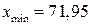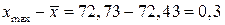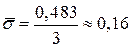II. Вычисление оценок математического ожидания и дисперсии

Поиск по сайту