Для построения гистограммы заполним последний столбец таблицы 1. Строим точки с координатами 
.
Если построенные точки гистограммы соединим плавной линией (на рис. 1 – пунктирная линия), то эта линия будет аналогом плотности распределения случайной величины и, следовательно, по виду гистограммы можно выдвинуть предположение о виде закона распределения случайной величины.
Таблица 1
| Статистическое распределение выборки | 
| 
| 
| 
| 
| |||
| № класса | Границы классов | 
| 
| |||||
| (71,95; 72,07) (72,07; 72,19) (72,19; 72,31) (72,31; 72,43) (72,43; 72,55) (72,55; 72,67) (72,67; 72,79) | 1/60 3/60 10/60 17/60 15/60 10/60 4/60 | 72,01 72,13 72,25 72,37 72,49 72,61 72,73 | –3 –2 –1 | –3/60 –6/60 –10/60 15/60 20/60 12/60 | 9/60 12/60 10/60 15/60 40/60 36/60 | 0,14 0,42 1,39 2,36 2,08 1,39 0,56 | ||
| 
| 
|
В нашем примере по виду гистограммы (рис. 1) выдвигаем гипотезу о нормальном распределении (или о распределении, близком к нормальному) случайной величины с плотностью 
.
IV. Проверка гипотезы о нормальном распределении случайной величины
Ввиду ограниченного числа наблюдений статистический закон распределения обычно в какой-то мере отличается от теоретического, даже если предположение о законе распределения сделано правильно. В связи с этим возникает необходимость решить следующую задачу: является ли расхождение между статистическим и теоретическим законами распределения следствием ограниченного числа наблюдений или оно является существенным и связано с тем, что действительное распределение случайной величины не соответствует выдвинутой гипотезе.
Для проверки гипотезы о нормальном распределении рассматриваемой величины заполняем таблицу 2.
1. Производим новую классификацию выборки: объединяем интервалы, для которых 
в один. В нашем примере после объединения 
.
2. Вычисляем вероятности 
попадания варианты в каждом интервале по формуле 
, где 
– номер интервала, 
– функция Лапласа.
3. Вычисляем 
и с учетом объединения интервалов.
4. В нашем примере 
.
5. По заданному уровню значимости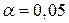 
и числу степеней свободы 
по таблице находим 
.
6. Так как 
, то нет оснований отвергнуть выдвинутую гипотезу, т.е. гипотезу о том, что случайная величина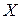 
распределена по нормальному закону, можно с надежностью 
считать правдоподобной, не противоречащей опытным данным.
Таблица 2
| Границы классов | 
| 
| 
| 
|
|
| 
| 
| 
| 
|
| (71,95;72,31) | –3,00 | –0,4987 | –0,75 | –0,2734 | 0,2253 | 0,2333 | 13,518 | 0,482 | 0,017 | ||
| (72,31;72,43) | –0,75 | –0,2734 | 0,00 | 0,0000 | 0,2734 | 0,2833 | 16,404 | 0,596 | 0,022 | ||
| (72,43;72,55) | 0,00 | 0,0000 | 0,75 | 0,2734 | 0,2734 | 0,2500 | 16,404 | –1,404 | 0,120 | ||
| (72,55;72,79) | 0,75 | 0,2734 | 2,25 | 0,4878 | 0,2144 | 0,2333 | 12,864 | 1,136 | 0,100 | ||
| Σ |  0,259
|
Итак, теоретическая плотность распределения имеет вид:
.
Построим график этой функции. Для этого возьмем 7 точек с абсциссами 
из таблицы 1 и вычислим ординаты этих точек. Составим таблицу 3.
Таблица 3
|
| 
| 
| 
| 
| 
|
| 72,01 72,13 72,25 72,37 72,49 72,61 72,73 | –0,42 –0,30 –0,18 –0,06 0,06 0,18 0,30 | 0,1760 0,0900 0,0324 0,0036 0,0036 0,0324 0,0900 | 3,52 1,80 0,65 0,07 0,07 0,65 1,80 | 0,0296 0,1650 0,5220 0,9320 0,9320 0,5220 0,1650 | 0,07 0,41 1,31 2,33 2,33 1,31 0,41 |
Примечания: 
, 
.
Для более точного построения графика найдём максимум и точки перегиба функции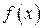 
: максимум 
, точки перегиба (72,27; 1,52) и (72,59; 1,52).
Строим график 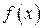на рис. 1 (сплошная линия).
Сравним теоретическую и эмпирическую плотности распределения случайной величины:
Таблица 4
| № | |||||||
|
| 72,01 | 72,13 | 72,25 | 72,37 | 72,49 | 72,61 | 72,73 |
|
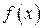
| 0,07 | 0,41 | 1,31 | 2,33 | 2,33 | 1,31 | 0,41 |
| 0,14 | 0,42 | 1,39 | 2,36 | 2,08 | 1,39 | 0,56 |
Сравнивая значения ординат плотности распределения случайной величины и плотности относительных частот, мы наблюдаем незначительное отклонение этих величин друг от друга, что также свидетельствует о правильности выбора закона распределения.