Арифметико-логические устройства (АЛУ) – это специализированные микросхемы, выполняющие в соответствии с программой на входах арифметические и логические преобразования двоичной информации. По сравнению с микросхемами, работающими по жесткой, наперед заданной программе, АЛУ представляют собой устройства более высокого класса. В микропроцессорной технике АЛУ являются базовыми элементами. Они используются в сочетании с регистрами сдвига, оперативными запоминающими устройствами и другими узлами. АЛУ дороже простых микросхем, однако благодаря универсальным свойствам применение их в аппаратуре во многих случаях оказывается оправданным. Микросхемы АЛУ, принадлежащие к разным видам логик, в частности к ТТЛ-типа К155ИП3 и КМОП-типа 564ИП3, функционально во многом совпадают, в том числе и по разводке выводов. Далее рассматриваться будет только микросхема К155ИП3 (смотри макет).
Микросхема К155ИП3 предназначена для действий с двумя четырехразрядными двоичными словами А = A3, A2, A1, A0 и B = B3, B2, B1, B0. Конкретный вид операции выполняемой микросхемой, задается пятиразрядным кодом на входах M, S3, S2, S1, S0. Всего это АЛУ способно выполнить 25 = 32 операции: 16 логических при М = 1 (И, И-НЕ, ИЛИ, ИЛИ-НЕ, исключающее ИЛИ и др.) и 16 арифметико-логических при М = 0 (сложение, вычитание, сравнение чисел и прочее).
На выходах F0, F1, F2, F3 формируются результаты логических преобразований и арифметических действий. На выходе переноса С4 образуется сигнал старшего (пятого) разряда при выполнении арифметических операций и логических действий. Дополнительные выходы – образования ускоренного переноса G и распространения ускоренного переноса Р используются только при организации многоразрядных АЛУ в сочетании с блоком ускоренного переноса К155ИП4.
Слова А и В, подлежащие обработке, могут быть представлены в положительной или в отрицательной логике. Таблицы истинности для каждого варианта логики различны.
В данной работе используется только положительная логика. Таблица истинности для этого варианта приведена ниже.
Практические задания
1. Записать по указанию преподавателя два четырехзначных двоичных числа А и В.
2. На действующем макете АЛУ убедиться в соответствии его работы таблице истинности. Для этого необходимо сначала на бумаге для пары чисел А и В, данных преподавателем, произвести те арифметико-логические преобразования, которые указаны в таблице истинности. Заполнить таблицу результатов, приведенную ниже. В ней вместо F3, F2, F1, F0 должны стоять конкретные двоичные числа.
Таблица результатов
| № п/п | S3 | S2 | S1 | S0 | M = 1 | M = 0 | ||||||
| F3 | F2 | F1 | F0 | F3 | F2 | F1 | F0 | |||||
| … | ||||||||||||
| F3 | F2 | F1 | F0 | F3 | F2 | F1 | F0 |
Числа A и B (или, иначе говоря, слова) вводятся в АЛУ с помощью соответствующих переключателей. Все возможные операции с этими числами производятся на макете АЛУ путем набора кодов операций на входах S3, S2, S1, S0. Светящаяся лампочка обозначает единицу, не светящаяся – нуль. Результаты, полученные на бумаге и на макете должны совпадать.
В режиме С = 1; М = 0; S3, S2, S1, S0 = 0110 АЛУ работает (кроме выполнения операции А-В-1; см. таблицу) как цифровой компаратор, т. е. устройство, которое выдает сигнал при равенстве двух чисел. Индикация равенства чисел А и В происходит на выходе, обозначенном А = B, на котором появляется логическая единица (светящаяся лампочка).
Краткая сводка правил логических операций
с двоичными числами
Зададимся двумя произвольными четырехразрядными двоичными числами: А = 0111 и В = 0011.
1. Логическое сложение («ИЛИ», дизъюнкция)
Таблица истинности для двух аргументов будет выглядеть так:
| X 1 | X 2 | Y |
Логическая операция обозначается так:  . Все действия удобно делать столбиком:
. Все действия удобно делать столбиком:

В Булевой алгебре аргументы и функции могут быть только одноразрядными, поэтому условились, что для логического сложения многоразрядных чисел необходимо произвести операцию «ИЛИ» в каждом разряде чисел отдельно. Переносов в старший разряд нет. Это правило относится ко всем логическим операциям.
2. Логическое умножение («И», конъюнкция)
Таблица истинности для двух аргументов будет выглядеть так:
| X 1 | X 2 | Y |
Логическая операция обозначается так:  .
.
Для этой операции нужно поразрядно произвести операцию «И»:
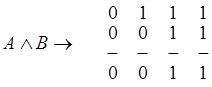
3. Логическая операция «исключающее ИЛИ»
Таблица истинности для двух аргументов будет выглядеть так:
| X 1 | X 2 | Y |
Логическая операция обозначается так: X 1Å X 2
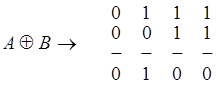
4. Арифметическая операция сложения
Таблица истинности для двух аргументов будет выглядеть так:
| А | В | C2 | C1 |
Эта операция обозначается так: А + В = С
Здесь С1 – младший разряд ответа, С2 – старший разряд ответа.

В отличие от Булевой алгебры, в арифметике переносы в старший разряд не запрещены, а в случае переполнения разряда – обязаны быть.
Контрольные вопросы
1. К каким схемам, комбинационным или последовательностным, относятся схемы АЛУ?
2. Что такое дополнительный код двоичного числа? Как он используется в двоичной арифметике?
3. Какое двоичное число больше: 001 111 101 или 010 010 011?
4. Что такое цифровой компаратор? Приведите пример его применения в технике.
Таблица истинности АЛУ К155 ИП3
Положительная логика (C = 1)
| S3, S2, S1, S0 | Логические операции M = 1 | Арифметико-логические операции M = 0 |

| 
| |

| 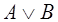
| |
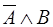
| 
| |
| лог. 0 | лог. 1 | |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 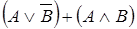
| |

| 
| |
| лог. 1 | 
| |

| 
| |

| 
| |

| 
|
Работа 7