Программирования
Стохастическое программирование позволяет по-новому подойти к решению задач, информационная структура которых (естественная или определяемая стохастическим расширением) известна заранее. Процесс решения задачи стохастического программирования может быть разделен на два этапа. Первый — предварительный этап — обычно весьма трудоемкий. На первом этапе строится закон управления — решающие правила или решающие распределения, связывающие решение или механизм формирования решения с реализованными значениями и заданными статистическими характеристиками случайных параметров условий задачи. Предварительный этап не требует знания конкретных реализаций значений параметров целевой функции и ограничений. Построение решающих правил или распределений требует лишь информации о структуре задачи и о некоторых статистических характеристиках случайных исходных данных. Поэтому процесс конструирования решающих механизмов не стеснен обычно недостатком времени и может начинаться с момента осознания важности задачи, как только построена стохастическая модель и проверено ее соответствие изучаемому явлению. Затраты времени и ресурсов на подготовку решающих правил или распределений обычно оправдываются. Полученные при этом законы управления позволяют решать не только отдельные конкретные задачи; они применимы для множества задач заданной информационной структуры. Решающие правила или распределения — это формулы, таблицы, инструкции или случайные механизмы с фиксированными или меняющимися в зависимости от реализации случайных параметров условий статистическими характеристиками. На втором этапе анализа стохастической модели решающие правила или распределения используются для оперативного решения задачи. Второй этап естественно называть оперативным этапом анализа стохастической модели. Заметим, что при отсутствии статистических характеристик случайных исходных данных можно заменить на предварительном этапе прямой путь построения решающих механизмов адаптивным — итеративным методом решения стохастической задачи по последовательным наборам реализаций случайных параметров условий задачи. Стохастическое программирование определяет новый подход к алгоритмизации управления в сложных системах. Математическое обеспечение сложных экстремальных управляющих систем целесообразно компоновать не из алгоритмов решения экстремальных задач, а из решающих правил соответствующих стохастических расширений. При этом формирование законов управления — решающих правил или решающих распределений — связывается не с оперативной работой, а с этапом проектирования управляющей системы. Стохастическое программирование и, в частности, стохастическое расширение открывают, таким образом, путь оперативного анализа сложных задач, альтернативой которому являются экспертные оценки и волевые решения.
Для решения задачи стохастического программирования в Р-постановке и с вероятностными ограничениями переходят к детерминированному эквиваленту.
Для целевой функции детерминированный эквивалент имеет вид:
· при минимизации целевой функции
 2.1
2.1
· при максимизации целевой функции
 2.2
2.2
где σ2j — дисперсия случайной величины сj Решение таких задач затруднительно, поэтому далее рассматриваем целевая функция только в М- постановке. Детерминированный эквивалент вероятностного ограничения типа (а)
 2.3
2.3
может быть сведен к виду:
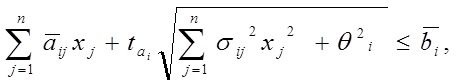 2.4
2.4
где ai j, bi — математические ожидания;, σ i j 2, ө i 2 — дисперсии случайных величин aij, bi; ta = Ф*-1(ai) — обратная функция нормального распределения при функции распределения:
 2.5
2.5
где ai — заданный уровень вероятности (табл. 2.1).
Обычно решают задачи при ai > 0,5, поэтому даны значения ta только для положительных ta..
Таблица 2.1
| ai | 0,5 | 0,6 | 0,7 | 0,77 | 0,84 | 0,89 | 0,93 | 0,96 | 0,98 | 0,987 | 0,994 |
| t a | 0,0 | 0,25 | 0,5 | 0,75 | 1,25 | 1,5 | 1,75 | 2,0 | 2,25 | 2,5 |
Если же ai < 0,5; то t1-a = - ta. Так, для а = 0,4; t0,4 = t(1-0,6) = - t 0, 6 =0,25.
Детерминированный эквивалент задачи СТП в М-по- становке имеет вид
 2.6
2.6
Из (2.6) следует, что для решения задачи стохастического программирования в М-постановке необходимы исходные данные, приведенные в предыдущей таблице.
Каждое 1-е ограничение в детерминированном эквиваленте (2.6) отличается от аналогичного ограничения задачи линейного программирования следующим:
 2.7
2.7
·  от детерминированных значений aij, bi выполнен переход к математическим ожиданиям случайных величин aij, bi;
от детерминированных значений aij, bi выполнен переход к математическим ожиданиям случайных величин aij, bi;
· появился дополнительный член (ζ)

который учитывает все вероятностные факторы: закон распределения с помощью ta; заданный уровень вероятности ai; дисперсии случайных величин aij равные σ ij 2; дисперсии случайных величин bi равные ө i 2.
Решение задач СТП
Детерминированный эквивалент задачи стохастического программирования в М-постановке включает ограничения, которые являются нееепарабельными функциями. Обозначим
 3.1
3.1
тогда задачу стохастического программирования можно записать в сепарабельной форме:
 3.2
3.2
где


Эта задача является сепарабельной задачей нелинейного программирования и может быть решена с помощью стандартных программных средств.
Функция F(x1, х2, хп) называется сепарабельной, если она может быть представлена в виде суммы функций, каждая из которых является функцией одной переменной, т. е. если 

Если целевая функция и функции в системе ограничений задачи нелинейного программирования сепарабелъные, то приближенное решение может быть найдено методом кусочно-линейной аппроксимации.
Пример 1. Рассмотрим задачу распределения двух видов ресурсов для выпуска двух наименований изделий.
Решение. Ее модель:


где a i j, bi, cj — случайные.
При М-постановке модель запишется:

где a1, a2 — заданные уровни вероятности соблюдения каждого ограничения.
Для того чтобы решить задачу в М-постановке, необходимо перейти к ее детерминированному эквиваленту:

Исходные данные, необходимые для решения этой задачи, сведены в таблицах 3.3 и 3.4.
Таблица 3.3
| Величина | С | d | D |
| X1 | |||
| X2 |
Таблица 3.4
| Ограничения | Случайные величины | |||||
| ai1 | ai2 | bi | ||||

| 
| 
| 
| 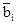
| 
| |
Если задать уровни вероятности a1,2 = 0,6, для которых ta = 0,25, то получим после подстановки исходных данных детерминированный эквивалент:

Результаты решения этой задачи для детерминированного случая ζ i = 0 и при a i = 0,6 (табл. 3.5), где

Таблица 3.5
| Величина | ζ i = 0 | a i = 0,6 | Величина | ζ i = 0 | a i = 0,6 |
| x1 | ζ1 | 4,4 | |||
| x2 | 5,3 | 5,04 | ζ2 | 5,8 | |
| L | 52,4 | 50,3 | γ1 | 4,4 | |
| β | γ2 | 5,1 |
Таблица 3.6
| Величина | a1,2 | |||||
| 0,5 | 0,6 | 0,77 | 0,89 | 0,96 | 0,987 | |
| x1 | 3,71 | 3,07 | 2,165 | |||
| x2 | 5,3 | 5,04 | 4,51 | |||
| L | 52,4 | 50,3 | 46,1 | 42,6 | 39,3 | 34,8 |
| β | 18,7 | 33,6 | ||||
| γ1 | 4,4 | 12,3 | 17,9 | 24,3 | 33,3 | |
| γ2 | 5,1 | 14,8 | 16,5 | 23,2 |
Рассмотрим теперь, как повлияют на результат решения задачи величины, определяющие ее вероятностный характер. К таким величинам относят заданный уровень вероятности ai, и дисперсий σij2 и θi2. Начнем с анализа влияния ai (табл. 3.6).
Из анализа решения этой задачи можно сделать следующие выводы: для обеспечения гарантированного (с вероятностью a = 0,6) выполнения плана необходимо иметь дополнительно около 5% каждого вида ресурса. При отсутствии дополнительного ресурса целевой функции может уменьшиться на величину (β = 4% вследствие возможного сокращения выпуска продукции х2 от 5,3 до 5,04.
Этот пример подтверждает тот факт, что в реальных условиях для гарантированного выполнения плана необходимы дополнительные ресурсы в размере ζ i противном случае возможно уменьшение выпуска продукции.
При этом можно сделать выводы:
· в целях повышения заданного уровня вероятности выполнения плана ai требуется увеличить дополнительные ресурсы γi. Так, для выполнения плана с вероятностью, близкой к 1 (а = 0,987), необходим дополнительный ресурс в размере γi = 26,..., 33% от величины используемого без учета вероятностных характеристик;
· отсутствие такого увеличения может привести к ухудшению целевой функции на величину β = 33,6%;
· возрастание a отражается на номенклатуре продукции. При этом в интервале a = 0,5,..., 0,77 значение х1 сохраняется неизменным, а х2 — уменьшается. При дальнейшем увеличении а = 0,89,..., 0,987 значение х2 = const, в то время как х1 сначала скачком растет, а затем постепенно уменьшается. Несмотря на то что при а = 0,89 значения x1,2 резко изменяются, целевая функция во всем интервале изменения а уменьшается плавно. Таково влияние заданного уровня вероятности соблюдения ограничений а на результат решения задачи.
Для большей реальности и выполнимости планов элементы модели должны постоянно уточняться по фактическим реализациям случайных величин.
Заключение
При написании курсовой работы по дисциплине «Математические методы» на тему «Стохастическое программирование » у меня возникали непонятности в теоритической части, так как каждый автор пишет по разному, но мне пришлось понимать и разбираться в каждой из книг.
Список литературы
1. «Математические методы в программировании »: / Агальцов В.П., Волдайская И.В. Учебник: – М.: ИД «ФОРУМ»: ИНФРА-М, 2006. – 224с.: ил. –(Профессиональное образование). – (Учимся программировать).
2. Лекции по дисциплине «Математические методы ».
3. «Математические методы: Учебник» / Партика Т.Л., Попов И.И. – М: ФОРУМ: ИНФРА, 2005.
4.Интернет сайт: https://ru.wikipedia.org/wiki/
5.«Математическое программирование» / Костевич Л., издательство «Новое знание», 2003.