Вопросы для подготовки к экзамену
IV семестр
1. События. Виды событий. Вероятность события. Классическое определение вероятности. Относительная частота. Устойчивость относительных частот.
2. Сумма и произведение событий. Условная вероятность. Теоремы сложения и умножения вероятностей.
3. Формула полной вероятности.
4. Формула Байеса.
5. Задача о повторении опытов. Формула Бернулли.
6. Случайная величина. Дискретная случайная величина. Ряд распределения. Многоугольник распределения.
7. Биномиальное распределение. Распределение Пуассона.
8. Простейший поток событий. Свойства. Примеры.
9. Математическое ожидание. Дисперсия. Среднее квадратическое отклонение. Определения. Свойства.
10. Неравенство Чебышева.
11. Теорема Чебышева.
12. Теорема Бернулли.
13. Функция распределения. Определение. Свойства. График.
14. Закон равномерного распределения вероятностей. Определения. Примеры. Свойства. Числовые характеристики.
15. Нормальное распределение. Определение. Примеры. Свойства. Числовые характеристики. Кривая Гаусса. Правило трех сигм.
16. Показательное распределение. Определения. Примеры. Числовые характеристики.
1 7. Задачи математической статистики. Генеральная и выборочная совокупности. Статистическое распределение выборки. Эмпирическая функция распределения. Полигон и гистограмма.
18. Статистические оценки параметров распределения. Генеральная и выборочная средние. Оценка генеральной средней по выборочной средней.
19. Генеральная выборочная исправленная дисперсии.
20. Точность оценки. Доверительный интервал.
21. Статистические гипотезы. Ошибки первого и второго рода. Отыскание критической области. Понятие о критериях согласия.
Экзаменационный билет № 1
1. События. Виды событий. Вероятность события и ее свойства.
2. Математическое ожидание. Дисперсия. (непрерывная случайная величина).
3. При разрыве снаряда образуются 10% крупных осколков, 60% средних и 30% мелких. Вероятность пробивания брони крупным осколком – 0,7, средним – 0,2 и мелким – 0,05. Известно, что в броню попал осколок. Найти вероятность того, что броня пробита.
Экзаменационный билет № 2
- Перестановки. Размещения. Сочетания.
- Закон равномерного распределения вероятностей. Определения. Примеры. Свойства. Числовые характеристики.
- Стрелок, имея 3 патрона, стреляет в цель до первого попадания (или пока не израсходует все патроны). Вероятность попадания при каждом выстреле равна 0,6. Составить ряд распределения случайной величины Х – числа произведенных выстрелов.
Экзаменационный билет № 3
1. Сумма событий. Теорема сложения вероятностей.
2.. Нормальное распределение. Определение. Примеры. Свойства. Числовые характеристики.
3. Найти математическое ожидание и дисперсию показательного распределения, заданного при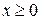 
плотностью 
.
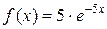Экзаменационный билет № 4
1. Произведение событий. Условная вероятность. Теорема умножения вероятностей.
2. Показательное распределение. Определения. Примеры. Числовые характеристики.
3. Найти математическое ожидание случайной величины X распределенной равномерно в интервале (2, 8).
Экзаменационный билет № 5
1. Формула полной вероятности.
2. Генеральная и выборочная совокупности. Статистическое распределение выборки. Эмпирическая функция распределения. Полигон и гистограмма.
3. Написать плотность вероятности нормально распределенной случайной величины X, зная, что M(X) = 3, D(X) = 16/
Экзаменационный билет № 6
1. Вероятность гипотез. Формулы Байеса.
2. Статистические оценки параметров распределения. Генеральная и выборочная средние. Оценка генеральной средней по выборочной средней.
3. Сколько различных чисел можно записать при помощи цифр 0, 1, 3, 4, 7?