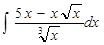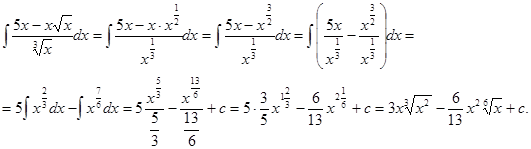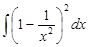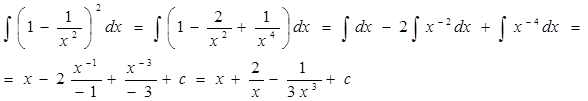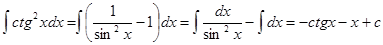Свойства неопределенного интеграла

1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:

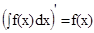
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т.е.

ò dF(x)=F(x) + C.

3. Постоянный множитель можно выносить за знак неопределенного интеграла:

ò af(x)dx = a ò fx)dx.

4. Неопределенный интеграл от алгебраической суммы функций равен такой же алгебраической сумме неопределенных интегралов от каждой функции:

ò (f (х) ± h (x)) dx = ò f (x) dx± ò h (x)dx.

Основные формулы интегрирования (табличные интегралы).

Из каждой формулы дифференцирования вытекает соответствующая ей формула интегрирования.

Ниже приведена таблица основных интегралов:

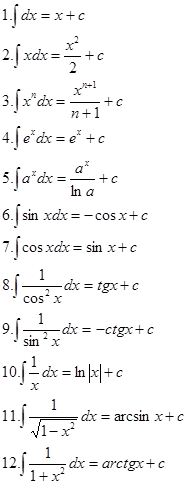
Непосредственное интегрирование. Под непосредственным интегрированием понимают такой способ инте­грирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции ихприменения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Пример1. Найти неопределённый интеграл

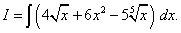
Решение. найдём данный интеграл как сумму трёх интегралов:

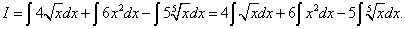
Все три полученные интеграла – табличны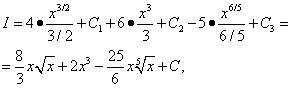е. где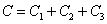

Пример2. Найти неопределённый интеграл .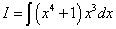

Решение. В подынтегральном выражении нужно умножить многочлен на одночлен, тогда получим сумму двух интегралов:

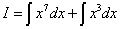. Применяем табличный интеграл, интегрируя степенные функции, и окончательный ответ: .

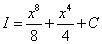Пример3.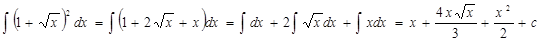

Пример4. Найти интеграл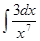

Решение:

Воспользуемся определением степени с отрицательным показателем (аⁿ¹1/аⁿ, а ¹ 0) и найдем неопределенный интеграл от степени:

.

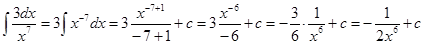Пример 5. Найти интеграл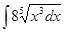

Решение. Воспользуемся определением степени с дробным показателем (а^m/n 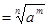, а>0) и найдем не­определенный интеграл от степени:

.

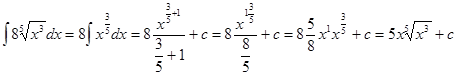Пример 6. Найти интеграл .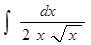

Решение:

Воспользуемся определением степени с дробным и отрицательным показателем и правилом умножения степеней с одинаковыми основаниями (а^т-а^п = =а^т+п) и найдем неопределенный интеграл от степени:

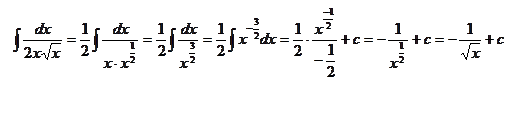Пример 7. Найти интеграл

Решение:

Воспользуемся определением степени с дробным показателем (а^т/^п= 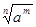, а>0), правилами действий над степенями с одинаковыми основаниями (а'^п*а^п=а^т+п, а'^п / а^п = а^т-п), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем

Заметим, что произвольные постоянные, входящие по определению в каждый из слагаемых неопределенных интегралов, объединяются в одну произвольную постоянную.

Пример 8.

Найти интеграл

Решение:

Раскроем скобки по формуле (а-b)² = а^2-2ab+b² и неопределенный интеграл от полученной алгебраической суммы функций заменим такой же алгебраической суммой неопределенных интегралов от каждой функции:

Пример 9. Найти интеграл òctg² xdx.

Решение:

Для нахождения интеграла воспользуемся формулой ctg² x=1/sin²x- 1 и свойствами неопределенного интеграла:

Алгоритм	Конкретное соответствие задания предложенному алгоритму.
1. .
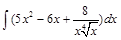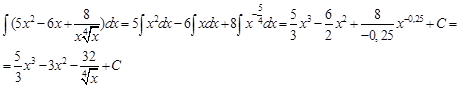
2.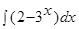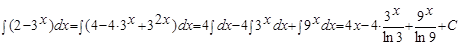