МНОГОМЕРНЫЙ АНАЛИЗ ДАННЫХ
Фундамент статистики как науки составляют эмпирические наблюдения за окружающим нас миром.
Одномерный статистический анализ представляет частный случай многомерного.
Практически все задачи одномерного анализа ставятся и решаются в предположении того, что в природе существует так называемый гауссовский закон распределения данных.
Регрессионный анализ
Основной целью регрессионного анализа является определение наличия и характера связи между переменными (в простейшем случае строится зависимость y(x) исходя из примерной формы кривой). Несколько лет назад американский Институт стратегического планирования провел исследование «Маркетинговая стратегия и уровень прибыли», в котором рассматривалось влияние наиболее значимых переменных на уровень прибыли компании. Выяснилось, что график зависимости рентабельности – у, от доли рынка – х, выглядит следующим образом (рис. 1):
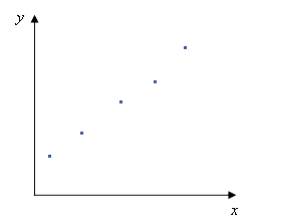
Рис. 1. График зависимости рентабельности от доли рынка
Невооруженным взглядом видно, что это прямая, однако точные ее пара- метры помогает установить регрессионный анализ. Регрессионный анализ широко используется в офисном пакете Excel, который предоставляет возможность исследовать не только линейные, но и другие, более сложные зависимости (в Excel это называется построением линий трендов).
Регрессионный анализ – метод установления аналитического выражениястохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется y при изменении любого из xi, и имеет вид: y=f(x1, x2,…,xn), где y – зависимая переменная (всегда одна); xi – независимые переменные (факторы) (их может быть несколько).
В ходе регрессионного анализа решаются две основные задачи: построение уравнения регрессии, т.е. нахождение вида зависимости между результатным показателем и независимыми факторами x1, x2,…, xn; оценка значимости полученного уравнения, т.е. определение того, насколько выбранные факторные признаки объясняют вариацию признака y.
Применяется регрессионный анализ главным образом для планирования, а также для разработки нормативной базы. В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение.
Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов, то регрессионный – одностороннюю зависимость, т.е. связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный.
Задача на использование методов корреляционного и регрессионного анализа.
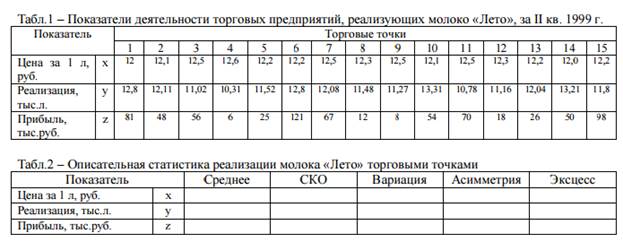
Наибольшим спросом в торговых точках города, реализующих молочную продукцию, пользуется молоко «Лето», выпускаемое в пакетах объемом 1 л. Цены за единицу этого товара в разных торговых точках варьируют. Известно, что реализация этого продукта вносит существенный вклад в общую выручку торговых точек. Возможно, она влияет и на величину прибыли предприятий торговли. Так ли это – установите с помощью анализа.
Корреляционный анализ
Корреляционный анализ позволяет судить о том, насколько похоже ведут себя разные переменные. В самом общем виде принятие гипотезы о наличии корреляции означает, что изменение значения переменной А произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут, то корреляция положительная; если одна переменная растет, а вторая уменьшается – корреляция отрицательная. При изучении корреляций стараются установить, существует ли какая- то связь между двумя показателями в одной выборке (например, между ростом и весом детей или между уровнем IQ и школьной успеваемостью) либо между двумя различными выборками (например, при сравнении пар близнецов), и если эта связь существует, то сопровождается ли увеличение одного показателя возрастанием (положительная корреляция) или уменьшением (отрицательная корреляция) другого.
Корреляционный анализ – метод установления связи и измерения ее тесноты между наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону. Корреляционной связью называется такая статистическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. Основной особенностью корреляционного анализа следует признать то, что он устанавливает лишь факт наличия связи и степени ее тесноты, не вскрывая причин. В статистике теснота связи может определяться с помощью различных коэффициентов (Пирсона, коэффициента ассоциации и т.д.), чаще используется линейный коэффициент корреляции между факторами x и y:
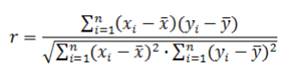
Значения коэффициента корреляции изменяются в интервале [-1; +1]. Значение r = –1 свидетельствует о наличии жестко детерминированной обратно пропорциональной связи между факторами; r =+1 соответствует жестко детерминированной связи с прямо пропорциональной зависимостью факторов. Другие значения коэффициента корреляции свидетельствуют о наличии стохастической связи, причем, чем ближе  к единице, тем связь теснее. При,
к единице, тем связь теснее. При,  <0,3 связь можно считать слабой; при
<0,3 связь можно считать слабой; при  - связь средней тесноты;
- связь средней тесноты;  - тесная.
- тесная.
Практическая реализация корреляционного анализа включает следующие этапы:
1) постановка задачи и выбор признаков;
2) сбор информации и ее первичная обработка (группировки, исключение аномальных наблюдений, проверка нормальности одномерного распределения);
3) предварительная характеристика взаимосвязей (аналитические группировки, графики);
4) устранение мультиколлинеарности (взаимозависимости факторов) и уточнение набора показателей путем расчета парных коэффициентов корреляции;
5) исследование факторной зависимости и проверка ее значимости;
6) оценка результатов анализа и подготовка рекомендаций по их практическому использованию.
Факторный анализ рассмотрен более подробно ввиду более широкого его использования.
Понятие «многомерный анализ данных»
Роль математических методов в любой области знания (не только в психологии) — представление эмпирических данных в пригодном для интерпретации виде, поиск смысла в исходной эмпирической информации.
Наследов А. Д. вводит понятие эмпирической математической модели (ЭММ), которые идентичны мыслительным операциям. Эти модели он называет описательными, так как они представляют данные, полученные в исследовании, в удобном для интерпретации виде.
Предлагаемая ниже классификация методов анализа данных проведена по двум основаниям: отсутствию или наличию независимых переменных, а также по типу зависимых и независимых переменных, которые могут быть качественными или количественными.
В регрессионном анализе наиболее явно виден функциональный характер модели анализа данных. Задача регрессионного анализа прямо формулируется как задача поиска функциональной зависимости Y от X, причем задача поиска формы связи не менее важна, чем вопросы статистической значимости полученных результатов. Наиболее широко применяется модель множественного линейного регрессионного анализа, позволяющая получать аналитически все стандартные статистические оценки.
Задачей дисперсионного анализа является установление связи между независимыми качественными переменными и зависимыми количественными. Однако поскольку функциональная структура связи очень проста - отклики представляются как линейные комбинации бинарных переменных - уровней факторов, то основное внимание в дисперсионном анализе уделяется вопросам статистической значимости влияния отдельных факторов.
Если отклики Y качественные, то для анализа используется группа методов, известная под общим названием распознавания образов. Наиболее используемым методом распознавания в случае количественных факторов является дискриминантный анализ. Примерами методов распознавания, ориентированных на случай качественных факторов, могут служить сегментационный анализ и метод обобщенного портрета.
Целью дискриминантного анализа является получение правила, позволяющего на основе наблюденных значений количественных независимых переменных X предсказывать значение качественной переменной Y, указывающей на принадлежность наблюдения к одному из заданных классов.
Сегментационный анализ состоит в последовательном разбиении совокупности наблюдений с целью получения, в конечном итоге, групп, максимально однородных по классовому составу.
Случай отсутствия зависимых переменных предполагает, что все анализируемые переменные в некотором смысле равноправны, и мы принимаем их за отклики (для простоты будем считать их количественными), значения которых определяются какими-то нам неизвестными факторами. Примерами могут служить морфологические или генетические характеристики растений, животных или людей, принадлежащих определенному таксону или обитающих на определенной территории. Задача анализа состоит в поиске этих неизвестных факторов. Выбор метода решения зависит от того, считаем ли мы искомые факторы качественными или количественными.
Для поиска качественных факторов используется группа методов, известная под названием кластерный анализ, среди которых наиболее часто используется так называемый агломеративно-иерархический метод, основанный на последовательном объединении многомерных наблюдений сначала в мелкие, а затем во все более и более крупные группы. Результатом кластерного анализа является разбиение всей совокупности наблюдений на классы. Полученной классификации соответствует качественная переменная (или несколько переменных, если используются несколько классификаций разной степени дробности или пересекающиеся классификации), категориями которой служат номера классов. Именно эта переменная (или переменные) и будет искомым качественным фактором. Найдя такой фактор (классифицирующую переменную), мы получаем возможность объяснять сходство или различие в значениях откликов для разных наблюдений принадлежностью их к одному или к разным классам.
Если же неизвестные факторы ищутся в форме количественных переменных, то используются методы факторного анализа. В этом случае задача состоит в представлении имеющихся откликов, Y, в виде линейных комбинаций неизвестных количественных факторов, X. С практической точки зрения применение этого метода оправдано, если удается с достаточной степенью приближения выразить большое количество откликов через малое число факторов. Одним из наиболее часто используемых методов этого класса является метод главных компонент, основанный на ортогональном проектировании исходного многомерного пространства в пространство меньшей размерности, в котором точки-наблюдения имеют наибольший разброс. Метод позволяет записать исходные данные в более компактном виде с сохранением максимума содержащейся в них информации и даже представить их графически на плоскости для случая двух факторов.
Следует еще раз подчеркнуть, что основным является деление методов анализа на те, в которых переменные делятся на зависимые и независимые (анализ связи), и те, в которых такого деления нет (анализ факторов). Дальнейшее деление методов по типу откликов и факторов довольно относительно. Дело в том, что уровни качественных факторов можно рассматривать как бинарные переменные, которые, в свою очередь, можно считать количественными переменными со значениями 0 и 1. С другой стороны, непрерывную шкалу значений количественной переменной можно категоризовать и рассматривать эту переменную как качественную. Во всяком случае, такого рода преобразования приходится делать вынужденно, когда по типу различаются не только факторы и отклики, но и разные переменные среди факторов или среди откликов.
Факторный анализ
Суть факторного анализа, состоит в том, чтобы имея большое число параметров, выделить малое число макропараметров, которыми и будут определяться различия между измеряемыми параметрами. Это позволит оптимизировать структуру анализируемых данных. Применение факторного анализа преследует две цели: сокращение числа переменных; классификация данных.
Факторный анализ довольно полезен на практике. Приведем несколько примеров.
Перед вами стоит задача исследовать имидж компании. Клиенту предлагается оценить данную компанию по целому ряду критериев, общее число которых может превышать несколько десятков. Применение факторного анализа в данном случае позволяет снизить общее количество переменных путем распределения их в обобщенные пучки факторов, например, «материальные условия компании», «взаимодействие с персоналом», «удобство обслуживания». Еще одним случаем применения данного метода может служить составление социально-психологических портретов потребителей. Респонденту необходимо выразить степень своего согласия/несогласия с перечнем высказываний о стиле жизни. В итоге, можно выделить, например, целевые группы потребителей: «новаторы», «прогрессисты» и «консерваторы».
Актуальным примером исследования в сфере банковского дела, может послужить, изучение уровня доверия клиента к банку, которое можно описать следующими факторами: — надежность сделок (включающий такие параметры, как сохранность средств, возможность беспрепятственного их перевода); — обслуживание клиентов (профессионализм сотрудников, их благожелательность) и — качество обслуживания (точность выполнение операций, отсутствие ошибок) и др.
Кластерный анализ Кластерный анализ (от англ. сluster – сгусток, пучок, гроздь) – это один из способов классификации объектов. Он позволяет рассматривать достаточно большой объем информации, сжимая его и делая компактными и наглядными. Термин «кластерный анализ» был введен в 1939 году английским ученым Р. Трионом, предложившим соответствующий метод, который сводился к поиску групп с тесно коррелирующим признаком в каждой из них. Целью кластерного анализа является выделение сравнительно небольшого числа групп объектов, как можно более схожих между собой внутри группы, и как можно более отличающихся в разных группах. В настоящее время разработано достаточно большое число алгоритмов кластерного анализа. Однако, попробуем объяснить его суть, не прибегая к строгому теоретизированию. Допустим, вы планируете провести опрос потребителей, (а все потребители разные), и вам, соответственно, необходимы различные стратегии для их привлечения. Для решения данной задачи мы предлагаем сегментировать клиентов, прибегнув к методу кластеризации.
Для этого выполняем следующие шаги:
формируем выборку и проводим опрос клиентов, определяем переменные (характеристики), по которым будем оценивать респондентов в выборке, вычисляем значения меры сходства и различия между ответами респондентов, выбираем метод кластеризации (т.е. правила объединения респондентов в группы), определяем оптимальное число кластеров (групп) в результате получаем таблицу следующего содержания:
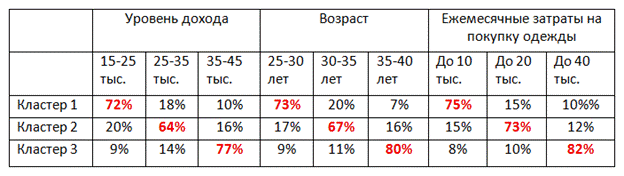
Информация, представленная в таблице, позволяет нам составить портрет клиентов каждого кластера, которые впоследствии необходимо учитывать при составлении стратегии успешного продвижения продукта на рынке.
Кластерный анализ хорошо зарекомендовал себя, и на сегодняшний день применяется в различных прикладных областях. В социологии: разделение респондентов на различные социально-демографические группы. В маркетинге: сегментация рынка по группам потребителей, группировка конкурентов по факторам конкурентоспособности. В менеджменте: выделение групп сотрудников с разным уровнем мотивации, выявление мотивирующих/демотивирующих факторов в организации, классификация конкурентоспособных отраслей и поставщиков, и др. В медицине — классификация симптомов, признаков заболеваний, пациентов, препаратов для успешной терапии. А также психиатрии, биологии, экологии, информатике и т.д.