Вычисление нормалей и углов отражения

Тема9. Построение реалистических изображений

В этом разделе мы рассмотрим методы, которые позволяют получить более-менее реалистичные изображения для объектов, моделируемых многогранниками и полигональными сетками.

Модели отражения света

Рассмотрим, как можно определить цвет пикселов изображения поверхности согласно интенсивности отраженного света при учете взаимного расположения поверхности, источника света и наблюдателя.

Зеркальное отражение света. Угол между нормалью и падающим лучом (Θ) равен углу между нормалью и отраженным лучом. Падающий луч, отраженный, и нормаль располагаются в одной плоскости (рис. 4.29).

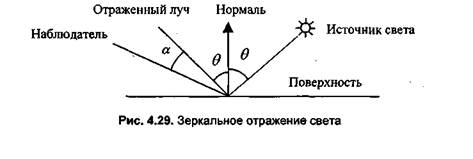
Поверхность считается идеально зеркальной, если на ней отсутствуют какие либо неровности, шероховатости. Собственный цвет у такой поверхности не наблюдается. Световая энергия падающего луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеивания не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0.5 мкм

Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны — чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие.

При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов, близких к 90 градусам.

Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемые по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых, относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cos а) ^p, где а — угол отклонения от линии идеально отраженного луча. Показатель р находится в диапазоне от 1 до 200 и зависит от качества полировки. Запишем это таким образом:

I_s=IK_scos^pa,

где I— интенсивность излучения источника, K_s — коэффициент пропорциональности, который изменяется от 0 до 1.

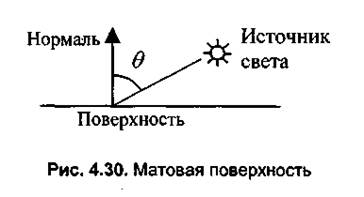
Диффузное отражение. Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны. Такой тип отражения характерен, например, для гипса, песка бумаги. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности (рис. 4.30).

 

I_d=I K_d cosq,

 

где I— интенсивность источника света, K_d — коэффициент, который учитывает свойства материала поверхности. Значение K_d находится в диапазоне от 0 до 1. Интенсивность отраженного света не зависит от расположения наблюдателя.

Матовая поверхность имеет свой цвет. Наблюдаемый цвет матовой поверхности определяется комбинацией собственного цвета поверхности и цвета излучения источника света.

При создании реалистичных изображений следует учитывать то, что в природе, вероятно, не существует идеально зеркальных или полностью матовых поверхностей. При изображении объектов средствами компьютерной графики обычно моделируют сочетание зеркальности и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузной и зеркальной компонент:

 

I_отр=I (K_d cosq+K_scos^pa),

 

где константы K_d, K_S определяют отражательные свойства материала.

Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов Θ и а. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:

 

I_отр= I_а K_а+I (K_d cosq+K_scos^pa),

 

где I_а — интенсивность рассеянного света, К_а — константа, изменяется от 0 до 1.

Можно еще усовершенствовать модель отражения, если учесть то, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использование такого правила вызывает сложности, поэтому на практике часто реализуют модель, выражаемую эмпирической формулой:

 

I_отр= I_а K_а+I (K_d cosq+K_scos^pa)/(R+k),

 

где R — расстояние от центра проекции до поверхности, k — константа.

Как определить цвет закрашивания точек объектов в соответствии с данной моделью? Наиболее просто выполняется расчет в градациях серого цвет (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости. Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонент. Коэффициент! К_а и K_d различны для разных компонент — они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент K_s будет одинаковым для всех компонент цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонент.

 

Алгебра векторов

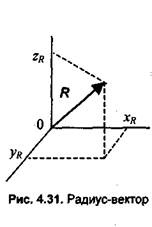
Здесь уместно сделать небольшое отступление от темы. Рассмотрим элементы алгебры векторов. Вектором называется отрезок прямой, соединяющий некоторые точки пространства А и В. Направление вектора — от начальной точки А к конечной точке В. Радиус-вектор R — это вектор, с начальной точкой в центре координат. Координатами радиус-вектора являются координаты конечной точки (рис. 4.31). Длина радиус-вектора часто называется модулем, обозначается как \ R|и вычисляется следующим образом:

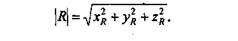
Единичный вектор — это вектор, длина которого равна единице. Перечислим основные операции над векторами.

1. Умножение вектора на число X = Va. Результат — вектор X, длина которого в а раз больше вектора V. Если число а положительно, то направление вектора X совпадает с вектором V. При а<0 вектор X имеет противоположное направление вектору V. Если V — это радиус-вектор, то координаты вектора результата будут (a*x_v, a*y_v, a*z_V), то есть каждая координата вектора умножается на число а.

2. Сложение векторов С = А+В. Результат сложения — это вектор, соответ­ствующий одной из диагоналей параллелограмма, сторонами которого являются векторы А и В (рис. 4.32). Все три вектора лежат в одной плоскости. Для радиус-векторов А и В координаты вектора С определяются так:

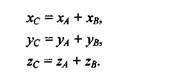
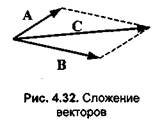
Разность двух векторов С = А - В можно определить через операцию сло­жения С = А + (-В). Вектор разности соответствует другой диагонали па­раллелограмма, изображенного на рис. 4.32. При вычитании радиус-векторов соответствующие координаты вычитаются:

3. Скалярное произведение векторов с = А*В. Результатом операции является число (скаляр), которое равно произведению длин векторов на косинус угла между ними:

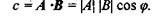
Если А и В — это радиус-векторы, то результат можно вычислить через координаты следующим образом:

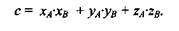
4. Векторное произведение векторов С = АхВ. Результатом операции является вектор, перпендикулярный к плоскости параллелограмма, образованного сторонами векторов А и В, а. длина вектора равна площади этого параллелограмма — подобно тому, как изображено на рис. 4.33.

В случае, когда векторы А и В являются радиус-векторами, координаты вектора результата С вычисляются по формулам:

Обратите внимание на то, что АхВ = -ВхА. Иными словами, порядок сомножителей определяет направление вектора результата.

В этом можно убедиться, если в формуле координат поменять местами координаты векторов А и В.

Кроме того, направление вектора результата операции АхВ зависит и от расположения координатных осей (система координат, изображенная на рис. 4.33, называется левой). Назовите ось у осью х, а ось х — осью y (получится правая система), а также соответственно поменяйте местами координаты х и у векторов А и В в формуле векторного произведения. В peзультате такой перестановки координаты вектора С поменяют знак, то есть вектор будет иметь противоположное направление.

Вычисление нормалей и углов отражения

Вычисление координат вектора нормали. Рассматривая модели отражения света, вы, наверное, обратили внимание на то, что нормаль к поверхности является важным элементом. Определение вектора нормали к поверхности заданной точке может быть выполнено различными способами. В значительной степени это определяется типом модели описания поверхности. Для поверхностей, заданных в аналитической форме, известны методы дифференциальной геометрии, которые основываются на вычислении частных производных функций описывающих поверхности. Например, если поверхность задана параметрическими функциями

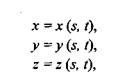
то координаты вектора нормали можно вычислить так:

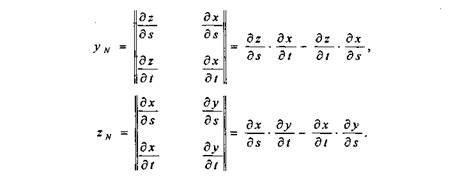
В случае описания поверхности векторно-полигональной моделью для определения нормалей можно использовать методы векторной алгебры.

Пусть в пространстве задана некоторая многогранная поверхность. Рассмот­рим одну ее плоскую грань в виде треугольника (рис. 4.34). Для вычисления координат вектора нормали воспользуемся векторным произведением любых двух векторов, лежащих в плоскости грани. В качестве таких векторов могут служить и ребра грани, например, ребра 1-2 и 1-3. Однако формулы для векторного произведения были определены нами только для радиус-векторов. Чтобы перейти к радиус-векторам, введем новую систему координат, центр которой совпадает с вершиной 1, а оси параллельны осям прежней системы.

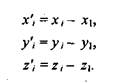
Теперь назовем ребро (1-2) вектором А, а ребро (1-3) — вектором В, как по­казано на рис. 4.35. Таким образом, положение нормали к грани в пространстве будет описываться радиус-вектором N. Его координаты в системе (х', у', z’ } выразим формулами для векторного произведения:

<!

Здесь использованы координаты вершин грани до переноса.

Плоская грань может изображаться в различных ракурсах. В каждой конкретной ситуации необходимо выбирать направление нормали, соответствующее видимой стороне грани. Если плоская грань может быть видна с обратной стороны, то тогда в расчетах отраженного света необходимо выбирать в качестве нормали обратный вектор, то есть (-N).

'Если полигональная поверхность имеет не треугольные грани, а, например плоские четырехугольные, то расчет нормали можно выполнять по любым трем вершинам грани.

 

Диффузное отражение. Определим косинус угла между вектором нормали направлением на источник света.

Первый пример (возможно, самый простой). Источник света располагается на оси z в бесконечности. Если расчеты производятся для видовой системы координат, то это означает, что источник света располагается на одной oси с камерой.

Косинус угла нормали к грани с осью z равен отношению координаты z и длины радиус-вектора

Второй пример. Источник света располагается в бесконечности и не лежит на оси z. В этом случае существенным является способ задания направления на источник света. Если расположение источника света описывать так же как и для камеры — двумя углами (а_с и β_c.), то можно сделать поворот координат так, чтобы ось z была направлена на источник света, и применить формулы для первого примера. Иными словами, необходимо преобразовать координаты вектора нормали. Здесь можно использовать тот факт, что длина вектора при повороте не изменяется, поэтому достаточно вычислить координату z_n в повернутой системе координат.

Если расположение источника света описывается вектором, направленным на источник света, то косинус угла с вектором нормали можно вычислить следующим образом. Вначале необходимо определить радиус-вектор, направленный на источник света. Обозначим его как S. Затем, для вычисления косинуса угла между радиус-векторами S и N воспользуемся формулами скалярного произведения векторов. Так как

Очевидно, что для упрощения вычислений целесообразно использовать век тор S единичной длины, то есть \S | = 1.

Третий пример. Источник света располагается в конечной точке пространства с координатами (х_с, у_c z_c). Для определения косинуса угла с нормалью вы полним сдвиг координат источника света так, чтобы вектор нормали в точке поверхности и вектор, направленный на источник света, выходили из общего центра. Выше мы уже рассматривали построение радиус-вектора нормали к треугольной грани путем сдвига (параллельного переноса) координат на (-x₁, -y₁, -z₁). Радиус-вектор, который направлен на источник света и который можно использовать для расчетов, будет иметь координаты (x_c-x₁, y_c-y₁, z_c-z₁ ). Затем уже можно вычислить искомый косинус угла через скалярное произведение радиус-векторов, как в предыдущем примере.

Зеркальное отражение. Будем считать, что задан радиус-вектор S, направленный на источник света, а также известен радиус-вектор нормали N. Требуется найти косинус угла между отраженным лучом и направлением камеры.

Вначале необходимо вычислить радиус-вектор отраженного луча. Обозначим его как R. Выполним некоторые геометрические построения, как показано на рис. 4.36.

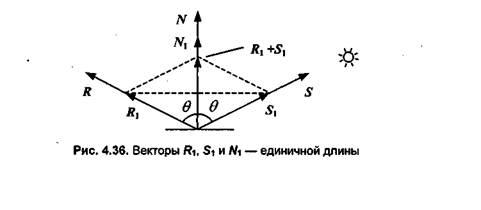
Для решения нашей задачи вначале рассмотрим единичные векторы R₁, S₁ и N₁. Поскольку векторы нормали, падающего луча и отраженного луча находятся в одной плоскости, то можно записать R ₁ + S ₁ = N', где N' — это вектор, соответствующий диагонали ромба и совпадающий по направлению с нормалью. Длина вектора N' равна 2cosΘ. Так как вектор N' по направление совпадает с N ₁, то

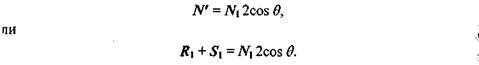
отсюда найдем единичный вектор отраженного луча:

Найдем cosΘ. Это можно сделать, используя скалярное произведение векторов N и S:

 

Подставим это значение в выражение для R ₁

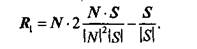
Полагая, что искомый вектор отраженного луча будет иметь такую же длину, что и вектор падающего луча, то есть R = \S\R ₁, получим

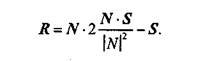
Это решение в векторной форме. Запишем координаты вектора R.

 

Осталось найти косинус угла между отраженным лучом и направлением камеры. Обозначим радиус-вектор, направленный на камеру, как К. Искомый косинус угла найдем, используя скалярное произведение векторов К и R:

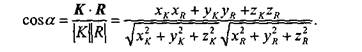
Очевидно, что для упрощения вычислений целесообразно задавать векторы S, N и K единичной длины (тогда и R будет единичным).

 

Метод Гуро

Этот метод предназначен для создания иллюзии гладкой криволинейной по­верхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Если каждая плоская грань имеет один постоянный цвет, определенный с учетом отражения, то различные цвета соседних граней очень заметны, и поверхность выглядит именно как многогранник. Этот дефект можно замаскировать за счет увеличения количества граней при аппроксимации поверхности. Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней— такой эффект называется эффектом полос Маха. Поэтому для создания иллюзии гладкости нужно намного увеличить количество граней, что приводит к существенному замедлению визуализации — чем больше граней, тем меньше скорость рисования объектов.

Метод Гуро основывается на идее закрашивания каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем интерполяции цветов примыкающих граней. Закрашивание граней по методу Гуро осуществляется в четыре этапа.

- Вычисляются нормали к каждой грани.

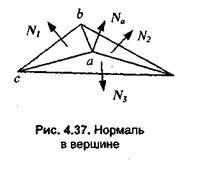
- Определяются нормали в вершинах. Нормаль в вершине определяется усреднением нормалей примыкающих граней (рис. 4.37).

 

- На основе нормалей в вершинах вычисляются значения интенсивностей в вершинах согласно выбранной модели отражения света.

- Закрашиваются полигоны граней цветом, соответствующим линейной. интерполяции значений интенсивности в вершинах

Вектор нормали в вершине (а) равен

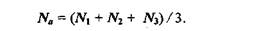
Определение интерполированных значений интенсивности отраженного света в каждой точке грани (и, следовательно, цвет каждого пиксела) удобно выполнять во время цикла заполнения полигона. Рассмотрим заполнение контура грани горизонталями в экранных координатах (рис. 4.38).

Интерполированная интенсивность I в точке (X,Y) определяется исходя из пропорции

Отсюда

Значения интенсивностей I₁и I₂ на концах горизонтального отрезка представляют собой интерполяцию интенсивности в вершинах:

! Метод Фонга

Аналогичен методу Гуро, но при использовании метода Фонга для определения цвета в каждой точке интерполируются не интенсивности отраженного света, а векторы нормалей.

-Определяются нормали к граням.

- По нормалям к граням определяются нормали в вершинах. В каждой точке закрашиваемой грани определяется интерполированный вектор нормали.

- По направлению векторов нормали определяется цвет точек грани в соот­ветствии с выбранной моделью отражения света.

Рассмотрим, как можно получить вектор нормали в каждой точке грани. Для интерполяции будем оперировать векторами N'_a, N'_b и N'_c, исходящими из центра координат плоскости проецирования и параллельными соответствующим нормалям N_a, N_b и N_c в вершинах а, в и с (рис. 4.39).

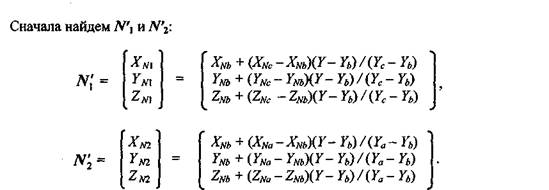
где, X_Na, Y_Na, Z_Na, X_Nb, Y_Nb, Z_Nb, X_Nc, Y_Nc и Z_Nc — координаты векторов N'_a, N'_b и N'_c. Теперь найдем координаты вектора N':

Вектор N' параллелен вектору N для нормали в точке (X, Y), поэтому eго можно использовать для расчета отражения света так же, как и вектор нормали N.

Метод Фонга сложнее, чем метод Гуро. Для каждой точки (пиксела) поверхности необходимо выполнять намного больше вычислительных операций. Тем не менее он дает значительно лучшие результаты, в особенности при имитации зеркальных поверхностей.

Общие черты и отличия методов Гуро и Фонга можно показать на примере цилиндрической поверхности, аппроксимированной многогранником (рис. 4.40). Пусть источник света находится позади нас. Проанализируем за крашивания боковых граней цилиндра.

На рис. 4.40 на закрашенной поверхности показаны черным цветом ребра
граней — это сделано для иллюстрации особенностей закрашивания, на самом деле после закрашивания никакого черного каркаса не будет, и поверхность выглядит гладкой.

Основные отличия можно заметить для закрашивания передней грани. Она перпендикулярна направлению лучей света. Поэтому нормали в вершинах этой грани располагаются симметрично— они образовывают попарно равные по абсолютной величине углы с лучами света. Для метода Гуро это обуславливает одинаковые интенсивности в вершинах передней грани. А раз интенсивности одинаковые, то и для любой точки внутри этой грани интенсивность одинакова (для линейной интерполяции). Это обуславливает единый цвет закрашивания. Все точки передней грани имеют одинаковый цвет, что, очевидно, неправильно.

Метод Фонга дает правильное закрашивание. Если интерполировать векторы нормалей передней грани, то по центру будут интерполированные нормали, параллельные лучам света (рис. 4.41).

По методу Фонга центр передней грани будет светлее, чем края. Возможно, это не очень заметно на типографском отпечатке рисунка данной книги, однако это именно так.