Матрицы. Операции над матрицами

Лекция 1.1 Матрицы и определители

Определение 1.1.1 Матрицей размера m ´ n называется прямоугольная таблица, состоящая из элементов некоторого множества (чисел, функций, векторов), имеющая m строк и n столбцов.

Положение каждого элемента в матрице однозначно определяется номером строки и номером столбца, на пересечении которых он находится.

Условно матрица может обозначаться следующим образом:

А = ил и , (1.1)

где i - номер строки, j - номер столбца на пересечении которых находится элемент матрицы . Числа m и n, указывающие количество строк и столбцов матрицы, называются размерами матрицы.

Виды матриц:

Ø матрицу называют квадратной порядка n, если m = n;

Ø матрица размера содержит только одну строку 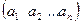и называется матрицей – строкой (n -мерной строкой);

Ø матрица размера 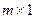содержит только один столбец 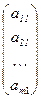и называется матрицей – столбцом (m -мерным столбцом);

Ø матрицу, состоящую из одного элемента, отождествляют с этим элементом ;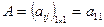

Ø квадратная матрица, для которой , называется симметрической;

Ø матрица, все элементы которой равны «0», называется нулевой (вырожденной):

Ø квадратная матрица порядка n вида называется диагональной:

Ø если в диагональной матрице 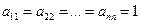, то эта матрица называется единичной .

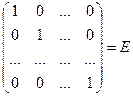Единичную матрицу любого порядка n удобно записывать, используя так называемый символ Кронекера: . Тогда

Определение 1.1.2 Две матрицы 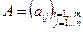и 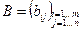называются равными, если их размеры совпадают и их соответствующие элементы равны, то есть .

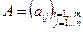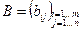Определение 1.1.3 Суммой двух матриц и называют матрицу того же размера, что и матрицы А и В, элементы которой .

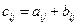Например, если и , то

Свойства: 1) А + В = В + А;
2) (А + В) + С = А + (В + С).

Замечание: Сложить можно только матрицы одного размера.

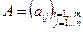Определение 1.1.4 Произведением числа на матрицу называется матрица , элементы которой .

Например, если и , то .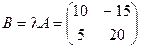

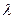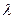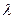Свойства: 1) (А + В) = В + А;
2) ;
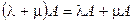3) .

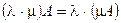Замечание: умножить на число можно матрицу любого размера.

Определение 1.1.5 Произведением матрицы 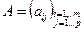на матрицу 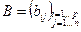называется матрица , элементы которой , где .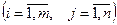

Замечание: Умножение матрицы А на матрицу В возможно только тогда, когда число столбцов матрицы А равно числу строк матрицы В. Если матрицы квадратные, то они должны иметь одинаковый порядок.

Например, если 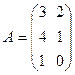и , то

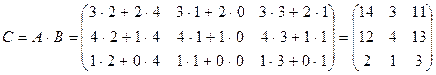
Свойства: 1) в общем случае;
2) ;
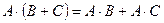3) ;
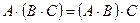4) ;
5) ;
6) .

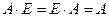Например, если , , то

Таким образом, единичная матрица играет роль единицы в действиях над матрицами.

Всякую квадратную матрицу А можно умножить саму на себя, т.е. найти матрицу . Эта матрица называется квадратом матрицы и обозначается .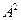
Аналогично, .
Исходная матрица А называется матрицей первой степени .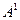
Нулевой степенью матрицы А называется единичная матрица Е, т.е. .
Свойства: 1) ; 2)

Определение 1.1.6 Транспонированием матрицы называется операция, в результате которой образуется новая матрица, полученная путем замены строк матрицы 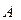её столбцами с сохранением номеров =

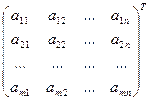Для элементов транспонированной матрицы верно равенство .

Например, если , то . В частности, операция транспонирования не изменяет симметрическую матрицу. Матрицу-строку размера переводит в матрицу-столбец размера 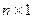и наоборот.

Свойства: 1) ;
2) ;
3) .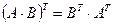