Для квадратных матриц существует специальная числовая характеристика, называемая детерминантом (или определителем). В общем виде определитель матрицы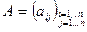 
представляется в виде массива n ´ n, состоящего из элементов матрицы А и обозначается «∆ » или detA.
А = 
detA = 
Элементы 
образуют главную диагональ определителя, элементы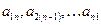 
- побочную диагональ.
Определение 1.2.1 Определителем квадратной матрицы второго порядка А = 
называется число detA =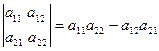 
, где числа 
- элементы определителя.
Таким образом, определитель второго порядка равен разности произведений его элементов главной и побочной диагоналей.
Пример1.2.1
∆ = 
,
Определение 1.2.2. Определителем для квадратной матрицы третьего порядка называется число detA = 
Определитель третьего порядка (n = 3) можно вычислить по правилу Саррюса
detA =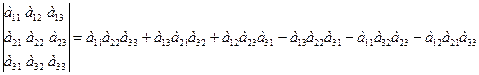 
,
Пример1.2.2
detA = 
,
Ø Суммой нескольких строк определителя называется строка, каждый элемент которой равен сумме соответствующих элементов этих строк.
Ø Произведением строки на число называется строка, каждый элемент которой равен произведению соответствующего элемента этой строки на данное число.
Ø Линейной комбинацией нескольких строк определителя называется строка, равная сумме произведений соответствующих элементов этих строк на некоторые числа.
Ø Минором 
элемента 
определителя порядка «n » называется определитель порядка «n-1 », полученный из определителя порядка «n » вычёркиванием строки с номером «i » и столбца с номером «j » на пересечении которых находится данный элемент.
Например, для элемента 
определителя 
минор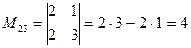 
Ø Алгебраическим дополнением данного элемента определителя называется минор этого элемента, взятый со знаком 
, где i, j – номер строки и номер столбца, на пересечении которых находится данный элемент 
.
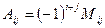Например, для элемента определителя алгебраическое дополнение имеет вид 
Свойства определителей
1º Если поменять местами строки и столбцы определителя, не меняя их порядка (транспонируя определитель), то определитель не изменит своё значение
,
2º При перестановке двух строк или двух столбцов определитель меняет свой знак
,
Для доказательства первого и второго свойств достаточно применить правило Саррюса и сравнить полученные результаты.
3º Определитель, у которого две строки или два столбца одинаковы, равен нулю.
Доказательство. Пусть определитель содержит два одинаковых столбца. Если эти столбцы поменять местами, то знак определителя должен измениться на противоположный:
∆ = -∆, 2∆ = 0, Þ ∆ = 0.
4º Если все элементы какого-либо столбца или строки равны нулю, то и сам определитель равен нулю.
5º Общий множитель какой-либо строки или столбца определителя можно выносить за знак определителя
Для доказательства этого свойства достаточно заметить, что определитель выражается в виде суммы, каждое слагаемое которой содержит множителем один элемент из каждой строки (столбца).
6º Если элементы какой-либо строки или столбца определителя пропорциональны элементам другой строки (столбца), то такой определитель равен нулю.
Это свойство является следствием свойств 3 и 5. Если вынести общий множитель одной из пропорциональных строк, то мы получим определитель, содержащий одинаковые строки. Такой определитель равен нулю.
7º Если элементы какой-либо строки или столбца определителя представляют собой суммы двух слагаемых, то определитель можно представить в виде суммы двух соответствующих определителей
.
(Для доказательства достаточно применить правило Саррюса).
8º Величина определителя не изменится, если к элементам какой-либо строки или столбца прибавить элементы другой строки (столбца), умноженные на одно и тоже число. 
Следствие: Если к строке (столбцу) определителя прибавить линейную комбинацию нескольких других строк (столбцов), то значение определителя не изменится.
9º Если одна из строк (столбцов) определителя есть линейная комбинация других строк (столбцов), то определитель равен нулю.
Справедливо и обратное утверждение: если определитель порядка «n» равен нулю, то одна из его строк есть линейная комбинация других строк.
10º Сумма произведений элементов какого-либо столбца или строки на алгебраические дополнения соответствующих элементов другого столбца или строки равна нулю.
Используя введённые понятия и свойства, сформулируем основное правило вычисления определителейпорядка «n » – правило Лапласа.
Определение 1.2.3 Определитель равен сумме произведений элементов любой его строки (столбца) на соответствующие им алгебраические дополнения
.
Пример 1.2.3
Вычислить определитель с помощью правила Лапласа:
Объем вычислений можно сократить, обнулив часть элементов той строки (столбца), по которым в последующем планируется разложить определитель при вычислении по правилу Лапласа.
∆ = 
