Основные уравнения фильтрации двухфазной жидкости

X. ОСНОВЫТЕОРИИ ФИЛЬТРАЦИИ МНОГОФАЗНЫХ СИСТЕМ

Общие положения; характеристики фильтрации многофазных систем

Ранее нами были рассмотрены различные задачи фильтрации однородных жидкостей и поршневое вытеснение одной жидкости другой. В действительности же в большинстве случаев картина течения много сложнее, так как в пористой среде может двигаться не одна однородная жидкость, а несколько жидкостей с различными физико-химическими характеристиками (вязкостью, плотностью и др). Как известно, идеального поршневого вытеснения одной жидкости другой, например, нефти водой, не существует; по мере продвижения первоначальной границы раздела эта граница становится нечеткой и образуется так называемая переходная зона, в которой остается невымытая нефть (остаточная нефть). Постепенно остаточная нефть вымывается вторгшейся водой и, таким образом, возникает двухфазная фильтрация, например, нефти и воды. Если при этом в поток вторгается и свободный газ (например, из газовой шапки) или выделяется растворенный газ из нефти в виде пузырьков, тогда механизм движения еще более усложняется. В этом случае одновременно движутся нефть, газ и вода, т.е. проявляется трехфазная фильтрация.

Процесс течения еще больше усложняется, если происходят химические реакции или фазовые превращения (конденсация или испарение) между компонентами смеси и к тому же проявляют себя капиллярные силы. Все эти обстоятельства затрудняют теоретические исследования задач фильтрации многофазных систем. Аналитически решения таких задач носят приближенный характер и оцениваются экспериментальными исследованиями.

Главными характеристиками движения многофазных систем являются насыщенность и скорость фильтрации каждой фазы.

Насыщенностью 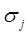порового пространства j-той фазой называется доля объема пор , занятая этой фазой в элементарном объеме:

j=1,2,3,…,n.

Очевидно, что . Следовательно, в n-фазной системе имеется (n-1) независимая насыщенность. В частности, при исследовании фильтрации смеси двух фаз используется лишь одна из насыщенностей, которая обозначается в дальнейшем (обычно это насыщенность вытесняющей фазы).

Экспериментально установлено, что при многофазной фильтрации закон Дарси может считаться справедливым для каждой из фаз в отдельности. Так, например, для 3-х компонентной системы (вода, нефть, газ) можно записать:

(10.1)

где - расход j-той фазы; - насыщенность порового пространства j-той фазой (в долях единицы); - фазовая проницаемость j-той фазы; - давление j-той фазы.

В дальнейшем для простоты и лучшего понимания сути физических процессов будем рассматривать процесс двухфазной фильтрации (например, воды и нефти или воды и газа).

Давления в фазах Р₁ и Р₂, вообще говоря, не равны друг другу из-за капиллярных эффектов, приводящих к скачку давления на границе раздела фаз, т.е.

, (10.2)

где Р₁ – давление вытесняющей (более смачивающей) фазы;

Р₂ – давление вытесняемой (не смачивающей твердые зерна породы) фазы;

т.е. большее давление Р₂ будет на стороне жидкости, не смачивающей твердые зерна породы.

Обычно предполагают, что капиллярное давление при совместном течении жидкостей совпадает с капиллярным давлением в равновесном состоянии для того же значения насыщенности. Поэтому будем считать, что при движении капиллярное давление можно представить в виде известной экспериментальной функции насыщенности

, (10.3)

где - коэффициент межфазного поверхностного натяжения;

- статический краевой угол смачивания между жидкостями и породой;

m – коэффициент пористости;

- безразмерная функция Леверетта.

Капиллярные силы создают в пористой среде перепад давления, величина которого ограничена и не зависит от размеров области фильтрации. В некоторых случаях можно пренебречь капиллярным скачком , тогда в приближенных расчетах можно принять . Так как наибольшее влияние на фазовую проницаемость оказывает насыщенность, то принимают . При этом очевидно, что . Для двухфазной жидкост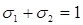и или , т.е. насыщенность первой фазой (вода) однозначно определяет насыщенность второй фазой (нефть). Следовательно, фазовые проницаемости К₁ и К₂ могут быть представлены как функции насыщенности первой (вытесняющей) фазой .

Если k- коэффициент проницаемости для однородной жидкости, тогда относительные фазовые проницаемости записываются соотношениями:

(10.4)

где и .

Тогда фазовые проницаемости для (10.1) будут иметь вид:

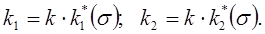
Типичный вид экспериментальных кривых относительных фазовых проницаемостей приведен на рис. 64, где по оси абсцисс отложены значения насыщенности вытесняющей фазы (воды).

Рис. 64

Движение этой фазы возможно, как это видно из графиков тогда, когда выполняется условие . Здесь - доля связанной (погребенной) воды, величина которой составляет 20¸22%. Для второй фазы связанная насыщенность равна (1-s_В) и называется остаточной нефтенасыщенностью. Таким образом, совместное течение двух фаз возможно только в интервале изменения насыщенности жидкостью (водой) .

Сумма относительных фазовых проницаемостей для каждого значения насыщенности s всегда меньше единицы, т.е.

Основные уравнения фильтрации двухфазной жидкости

Рассмотрим совместное изотермическое течение двух фаз в однородной пористой среде без фазовых переходов и химических реакций. Система уравнений, описывающая совместную фильтрацию фаз, строится на основе уравнений неразрывности для каждой фазы, уравнений движения (закона фильтрации) и соответствующих замыкающих соотношений.

Для вывода уравнения неразрывности в случае одномерного движения в трубке тока переменного сечения рассмотрим баланс первой фазы. В элемент объема длиной dx за время dt втекает объемное количество первой жидкости, равное , а вытекает:

где - накопление жидкости в элементе за единицу времени.

Насыщенность рассматриваемого элемента при этом меняется от s до

Поскольку объем порового пространства равен , то приравнивая накопление жидкости изменению насыщенности, помноженному на этот объем, получаем:

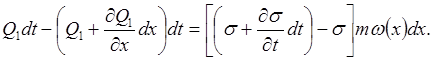
Откуда следует:

(10.5)

Для второй фазы (вытесняемой нефти) аналогично находим:

(10.6)

Складывая (10.5) и (10.6), получаем:

или (10.7)

Последнее равенство (10.7) показывает, что объемный расход двухфазной несжимаемой жидкости (смеси) от x не зависит.

В общем случае при наличии массовых сил, пользуясь законом Дарси, зависимостью капиллярного скачка Р_К от насыщенности s и уравнением неразрывности, получаем следующую систему уравнений:

(10.8)

где Х – проекция ускорения массовых сил на направление течения (оси x);

r₁ и r₂ – плотность вытесняющей и вытесняемой жидкости соответственно;

- капиллярный скачок, как функция насыщенности, определяемый по экспериментальным кривым.

Так как число неизвестных (Р₁, Р₂, Q₁, Q₂, s) равно пяти, то уравнения (10.8) образуют замкнутую систему.

Без принципиальных затруднений решается задача установившегося движения двухфазной смеси, когда расходы, давления и насыщенности не зависит от времени. Из уравнений неразрывности (10.5) и (10.6) следует, что в этом случае расходы Q₁ и Q₂ постоянны. Из системы (10.8) получаем два уравнения для производных:

(10.9)

(10.10)

Подставляя (10.9) в (10.10) получаем для s обыкновенное дифференциальное уравнение первого порядка:

(10.11)

Полученное уравнение легко интегрируется при Х=0 (отсутствие массовых сил); после чего устанавливается распределение насыщенности Затем из уравнений движения в системе (10.8) определяются давления Р₁ и Р₂ каждой фазы.

Теория Баклея-Леверетта

Баклей и Леверетт рассмотрели двухфазную фильтрацию, пренебрегая капиллярным давлением и массовыми силами, для одномерного прямолинейного движения несжимаемой смеси для случая . Тогда система (10.8) и уравнения (10.7) принимают вид:

; ; (10.12)

; ; (10.13)

; . (10.14)

Здесь V₁ и V₂ – скорости фильтрации соответственно первой (вытесняющей) и второй (вытесняемой) фаз (жидкостей).

Предположим, что суммарный расход жидкостей 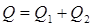постоянный, тогда при имеем

. (10.15)

В соответствии с этим из уравнений (10.12) и (10.14) находим

. (10.16)

Подставляя выражение (10.16) в первое уравнение (10.12), получаем

, (10.17)

где - так называемая функция Баклея-Леверетта:

. (10.18)

Дифференцируем (10.17) по х и подставляем полученный результат в первое уравнение неразрывности (10.13), получаем

. (10.19)

Уравнение (10.19) есть квазилинейное дифференциальное уравнение первого порядка в частных производных, которое обычно интегрируется методом характеристик.

Выпишем систему обыкновенных дифференциальных уравнений, соответствующую уравнению (10.19):

Независимая система ее первых интегралов есть:

; .

Отсюда следует, что при t = 0 расстояние - начальное распределение насыщенности. Тогда решением уравнения (10.19) будет

. (10.20)

Таким образом с помою решения (10.20), зная положение точки с насыщенностью s в момент t = 0, можно определить ее положение в любой момент времени t > 0.

Дифференцируя (10.20) по времени t, находим

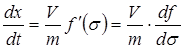. (10.21)

Нетрудно заметить, что выражение (10.21) представляет собой скорость распространения насыщенности заданной величины s.

Вид кривых и , построенных по формуле (10.18) с помощью графиков (рис.64), представлен на рис.65.

Рис.65

Физической особенностью модели Баклея-Леверетта для двухфазной фильтрации является зависимость скорости распространения того или иного значения насыщенности s от величины этой насыщенности. Это явление называется дисперсией волн. Действительно, в выражении (10.21) в ее правой части зависит от s. Эта зависимость изображена на рис.65, из которого видно, что при значениях насыщенности ( - насыщенность, соответствующая точке перегиба графика функции ) большие значения насыщенности s распространяются с большими скоростями (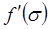 возрастает), а при наоборот – большие значения насыщенности s распространяются с меньшими скоростями ( убывает). Поэтому, имея начальное распределение насыщенности , представленное на рис.66, с течением времени профиль распределения насыщенности довольно резко изменяется, поскольку большие значения насыщенности s «догоняют» меньшие ее значения. Происходит в конечном итоге «опрокидывание» волны насыщенности и возникает неоднозначность в распределении : одному и тому же значению х соответствуют три значения насыщенности - , что физически абсурдно, так как в каждом сечении пласта в каждый момент времени может существовать только одна вполне определенная насыщенность s. Такая неоднозначность и устраняется введением скачка насыщенности (линия 1-3-5) из условия равенства площадей сегментов (1-2-3) и (3-4-5). Заметим дополнительно, что возникновение (зарождение) скачка насыщенности происходит в момент t^*, когда касательная к кривой стано

вится вертикальной.

Рис.66

Вполне очевидно, что скачок насыщенности представляет собой понятие математическое, не имеющее место в реальных условиях. В действительности же существует конечная длина d (рис.67), где значение насыщенности падает от σ_ф до нуля перед фронтом вытеснения. Размер этой зоны (d) зависит от капиллярных свойств среды и по сравнению с «переходной зоной» – зоной смеси (1+2) очень мал; поэтому в расчетах этой зоной часто пренебрегают (d = 0) и рассматривают лишь переходную зону.