Вычисление площадей плоских фигур
В прямоугольных координатах площадь криволинейной трапеции, расположенной «выше» оси абсцисс (f (x)≥ 0), равна соответствующему определенному интегралу (рис. 4.1):
Если криволинейная трапеция расположена «ниже» оси 0 x (f (x)<0), то ее площадь может быть найдена по формуле: 
. Эти формулы можно объединить в одну: 
Если плоская фигура имеет «сложную» форму, то прямыми, параллельными оси 0 y, ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.
Если криволинейная трапеция ограничена прямыми y=c и y=d, осью 0 y и непрерывной кривой 
, то ее площадь находится по формуле:
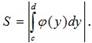
Площадь фигуры, ограниченной кривыми y= f 1(x), y= f 2(x) 
(см. рис. 4.1), прямыми x=a и x=b (a<b), можно найти по формуле
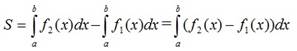
Пример 3. Вычислить площадь фигуры, ограниченной параболами
и 
Решение. Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений: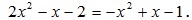 
Отсюда получаем квадратное уравнение 
с корнями x 1=1 и 
, представляющими собой пределы интегрирования.
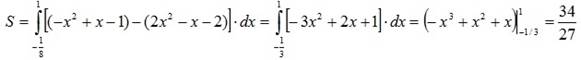
(единиц площади).
Вычисление длины дуги плоской кривой
Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y=f (x), где a≤x≤b.
Под длиной дуги 
понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина ее наибольшего звена стремится к нулю. Если функция y=f (x)и ее производная 
непрерывны на отрезке [ a;b ], то кривя AB имеет длину, равную
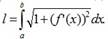
Пусть кривая AB задана уравнением в полярных координатах r=r (φ), α ≤ φ ≤ β. Предположим, что 
непрерывны на отрезке [ α;β ]. Тогда длину AB можно вычислить по формуле:
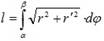
Пример 4. Найти длину окружности радиуса R.
Решение.Сначала найдем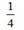 
длины дуги окружности 
от точки (0; R) до точки (R;0). Так как
По формуле (4.60) получим:
Таким образом, длина окружности равна 2 πR (единиц длины). Заметим, что данная формула часто применялась в школьном курсе математики, но принималась без доказательства.
Вычисление объёмов тел
Допустим, что необходимо найти объём V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси 0 x: S=S (x), a ≤ x ≤ b. Тогда объём тела можно найти по формуле
которая называется формулой объёма тела по площадям параллельных сечений (рис. 4.5).
Пусть вокруг оси 0 x вращается криволинейная трапеция, ограниченная непрерывной линией y=f (x)≥0, отрезком a ≤ x ≤ b и прямыми x=a, x=b (a<b). Полученное при этом тело, называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси 0 x, проведенной через произвольную точку x оси 0 x 
, есть круг с радиусом y=f (x). Следовательно, 
Применяя формулу, получаем формулу вычисления объёма тела вращения
Если криволинейная трапеция ограничена графиком непрерывной функции x=φ (y) ≥ 0 и прямыми x=0, y=c, y=d (c<d), то объем тела, образованного вращением этой трапеции вокруг оси 0 y, равен:
Пример 5. Найти объём шара радиуса R.
Решение. Шар может быть получен при вращении вокруг оси 0 x окружности радиуса R. Проинтегрируем уравнение окружности 
от точки (– R;0) до точки (R;0):
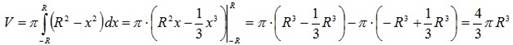(единиц объёма).
Экономическое приложение определенного интеграла
Рассмотрим одну из многочисленных задач экономики, решаемых с помощью определенного интегрирования.
Пусть функция z=f (x) описывает изменение производительности труда некоторого производства с течением времени. Тогда объём продукции 
, произведенной за период времени [ t 1 ;t 2], вычисляется по формуле:
Пример 6. Найти объём сливочного масла (кг), изготовленного молокоцехом за год (306 семичасовых рабочих дней), если ежедневная производительность этого цеха задана функцией 
где t – время в часах.
Решение. Найдем сначала объём V сливочного масла, произведенного молокоцехом за один семичасовой рабочий день (0 ≤ t ≤ 7):
Так как количество рабочих дней в году равно 306, то объём масла, произведенного за год, составит 
(кг) или V = 44 тонны 114 кг.