ИНТЕРФЕРЕНЦИЯ СВЕТА
 5.2.1. Принцип Гюйгенса
5.2.1. Принцип Гюйгенса
С точки зрения геометрической оптики при падении света на преграду с отверстиями свет не может попадать в область геометрической тени. В действительности же световая волна распространяется в пространстве за преградой, т.е. в области геометрической тени, и это проникновение тем существеннее, чем меньше размер преграды. Если размеры преграды (щели, отверстия) сравнимы с длиной волны, законы геометрической оптики нарушаются.
 Качественно поведение света за преградой с отверстием объясняет принцип Гюйгенса, который позволяет построить фронт волны в момент времени
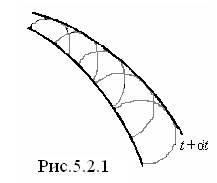
Качественно поведение света за преградой с отверстием объясняет принцип Гюйгенса, который позволяет построить фронт волны в момент времени  по известному положению фронта в момент времени t: каждая точка, до которой доходит волновое движение, служит центром вторичных волн (рис.5.2.1), огибающая этих волн дает положение фронта в следующий момент времени.
по известному положению фронта в момент времени t: каждая точка, до которой доходит волновое движение, служит центром вторичных волн (рис.5.2.1), огибающая этих волн дает положение фронта в следующий момент времени.
Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны (рис. 5.2.2). По Гюйгенсу каждая точка выделяемого отверстием участка волнового фронта служит центром вторичных волн, которые в изотропной и однородной среде будут сферическими. Построив огибающую, видим, что за отверстием волна проникает в область геометрической тени, огибая края преграды.
Интерференция световых волн
Рассмотрим две волны одинаковой частоты, которые, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления 
Амплитуда результирующего колебания в данной точке  где
где  .
.
Если разность фаз  возбуждаемых волнами колебаний остается постоянной во времени, волны называются когерентными. В случае некогерентных волн
возбуждаемых волнами колебаний остается постоянной во времени, волны называются когерентными. В случае некогерентных волн  непрерывно меняется, принимая с равной вероятностью любые значения, поэтому среднее за период значения
непрерывно меняется, принимая с равной вероятностью любые значения, поэтому среднее за период значения  равно нулю и
равно нулю и
 -
-
интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой волной в отдельности: 
В случае когерентных волн  имеет постоянное во времени, но свое для каждой точки пространства, значение, и
имеет постоянное во времени, но свое для каждой точки пространства, значение, и
 .
.
В точках пространства, где 
 , в точках, где
, в точках, где 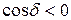
 . Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн. Если интенсивности обеих волн одинаковы, то в максимумах
. Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн. Если интенсивности обеих волн одинаковы, то в максимумах  , а в минимумах
, а в минимумах 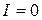 . Для некогерентных волн в этом случае интенсивность равна
. Для некогерентных волн в этом случае интенсивность равна  .
.
 Естественные источники не дают когерентного света. Это связано с тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Излучение производится цугами длиной до 3м, причем фаза одного цуга никак не связана с фазой следующего.
Естественные источники не дают когерентного света. Это связано с тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Излучение производится цугами длиной до 3м, причем фаза одного цуга никак не связана с фазой следующего.
Когерентные волны можно получить, разделив волну, излучаемую одним источником, на две части (рис.5.2. 3). Если заставить эти волны пройти разные оптические пути, а потом наложить друг на друга, наблюдается интерференция. Разность оптических путей, проходимых волнами, не должна быть очень большой, чтобы складываемые колебания принадлежали одному цугу волн.
Пусть разделение волн происходит в точке Р. До точки Р первая волна проходит в среде с показателем преломления 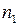 путь
путь  , вторая волна – в среде с показателем преломления
, вторая волна – в среде с показателем преломления  путь
путь  . Если в тоске О фаза колебаний равна
. Если в тоске О фаза колебаний равна  , то первая волна возбудит в точке Р колебание
, то первая волна возбудит в точке Р колебание 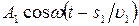 , а вторая волна – колебание
, а вторая волна – колебание  , где
, где  ,
,  - фазовые скорости волн. Разность фаз возбуждаемых в точке Р колебаний, равна
- фазовые скорости волн. Разность фаз возбуждаемых в точке Р колебаний, равна  Заменив
Заменив  , где
, где 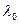 - длина волны в вакууме, имеем
- длина волны в вакууме, имеем  , где
, где  - оптическая разность хода.
- оптическая разность хода.
Если оптическая разность хода равна целому числу длин волн в вакууме,

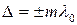 (т = 0,1,2….), (5.2.1)
(т = 0,1,2….), (5.2.1)
то разность фаз  будет кратна 2 π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в одной фазе, т.е. (5.2.1) – условие максимума интерференции.
будет кратна 2 π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в одной фазе, т.е. (5.2.1) – условие максимума интерференции.
Если  равна полуцелому числу длин волн в вакууме,
равна полуцелому числу длин волн в вакууме,
 (т = 0,1,2….), (5.2.2)
(т = 0,1,2….), (5.2.2)
то  , и колебания в точке Р будут в противофазе, т.е. (5.2.2) – условие минимума интерференции.
, и колебания в точке Р будут в противофазе, т.е. (5.2.2) – условие минимума интерференции.
Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников  и
и  , имеющих вид параллельных тонких светящихся нитей (рис.5.2. 4). Область, в которой эти волны перекрываются, называется полем интерференции. Во всей этой области наблюдается чередование максимумов и минимумов интерференции. Если в поле интерференции внести экран, на нем будет видна интерференционная картина, имеющая вид чередующихся темных и светлых полос. Вычислим ширину этих полос, если экран параллелен плоскости, проходящей через источники
, имеющих вид параллельных тонких светящихся нитей (рис.5.2. 4). Область, в которой эти волны перекрываются, называется полем интерференции. Во всей этой области наблюдается чередование максимумов и минимумов интерференции. Если в поле интерференции внести экран, на нем будет видна интерференционная картина, имеющая вид чередующихся темных и светлых полос. Вычислим ширину этих полос, если экран параллелен плоскости, проходящей через источники  и
и  . Положение точки на экране будем характеризовать координатой х, отсчитываемой в направлении, параллельном прямой
. Положение точки на экране будем характеризовать координатой х, отсчитываемой в направлении, параллельном прямой 
 , начало отсчета выберем в точке О, относительно которой
, начало отсчета выберем в точке О, относительно которой  и
и  расположены симметрично. На рис.5.2.4
расположены симметрично. На рис.5.2.4

Тогда
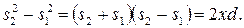
Для получения различимой интерференционной картины расстояние между источниками d должно быть значительно меньше расстояния до экрана  . Расстояние х, в пределах которого образуются интерференционные полосы, также много меньше
. Расстояние х, в пределах которого образуются интерференционные полосы, также много меньше  . Тогда
. Тогда  , и
, и  . Умножив
. Умножив  на показатель преломления среды п, получим оптическую разность хода
на показатель преломления среды п, получим оптическую разность хода
 . (5.2.3)
. (5.2.3)
Подставив (5.2.3) в (5.2.1) и (5.2.2), получаем координаты максимумов и минимумов на экране:

где  - длина волны в среде. Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между двумя соседними минимумами – шириной интерференционной полосы. Эти расстояния имеют одинаковые значения
- длина волны в среде. Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между двумя соседними минимумами – шириной интерференционной полосы. Эти расстояния имеют одинаковые значения
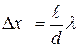 . (5.2.4)
. (5.2.4)
Согласно (5.2.4), расстояние между полосами растет с уменьшением расстояния между источниками d. При d, сравнимом с  , расстояние между полосами было бы того же порядка, что и
, расстояние между полосами было бы того же порядка, что и  . В этом случае отдельные полосы были бы совершенно неразличимы. Чтобы интерференционная картина была отчетливой, необходимо, чтобы
. В этом случае отдельные полосы были бы совершенно неразличимы. Чтобы интерференционная картина была отчетливой, необходимо, чтобы  .
.
Если интенсивность интерферирующих волн одинакова,  , то результирующая интенсивность в точках с разностью фаз
, то результирующая интенсивность в точках с разностью фаз  равна
равна
 .
.
Т.к.  , то согласно (5.2.3),
, то согласно (5.2.3),  растет пропорционально х. Следовательно, интенсивность меняется вдоль экрана по закону квадрата косинуса.
растет пропорционально х. Следовательно, интенсивность меняется вдоль экрана по закону квадрата косинуса.
Ширина интерференционных полос и расстояние между ними зависят от длины волны  . Только в центре картины, при х =0, совпадают максимумы всех длин волн. По мере удаления от центра максимумы разных цветов смещаются друг относительно друга все больше и больше. Интерференционная картина смазывается.
. Только в центре картины, при х =0, совпадают максимумы всех длин волн. По мере удаления от центра максимумы разных цветов смещаются друг относительно друга все больше и больше. Интерференционная картина смазывается.
Примеры решения задач
Задача 1.Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (λ 1=500нм) заменить красным (λ2 =650нм)?
Задача 2. Расстояния от бипризмы Френеля до узкой щели и экрана равны соответственно а =25см; b =100см. Бипризма стеклянная с преломляющим углом θ=20´. Найти длину волны света, если ширина интерференционной полосы на экране Δ х =0,55мм.
Задача 3. На тонкую пленку с показателем преломления п =1,33 падает параллельно пучок белого света. Угол падения θ1=52о. При какой толщине пленки зеркально отраженный свет будет наиболее ярко окрашен в желтый цвет (λ=0,60мкм)?
Задача 4. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R =8,6м, наблюдение ведется в отраженном свете. Радиус четвертого темного кольца (считая центральное темное кольцо за нулевое) r 4 =4,5мм. Найти длину волны падающего света.
ЗАДАЧА 3.Найти расстояние между полосами и число N полос интерференции, образованных бипризмой с показателем преломления n и преломляющим углом  , если длина волны источника l. Расстояние от источника света до бипризмы а, а от бипризмы до экрана b.
, если длина волны источника l. Расстояние от источника света до бипризмы а, а от бипризмы до экрана b.
ДАНО:
n
 λ
a
b
λ
a
b
|
N –?

|
АНАЛИЗ. Бипризма (рис. 5.2.7) представляет собой две призмы, изготовленные из одного куска стекла и имеющие одну общую грань. Преломляющий угол  каждой призмы мал, поэтому все лучи отклоняются призмой на практически одинаковый угол
каждой призмы мал, поэтому все лучи отклоняются призмой на практически одинаковый угол
j = (n – 1)  .
.
 Рис. 5.2.7
Рис. 2.2.5
Рис. 5.2.7
Рис. 2.2.5
|
В результате образуются две когерентные цилиндрические волны, исходящие из мнимых источников S 1и S 2, лежащих в одной плоскости с S.
РЕШЕНИЕ. Расстояние между источниками равно
d = 2 a sin j» 2 a j = 2 a (n – 1)  .
.
Расстояние от источников до экрана
 = а + b.
= а + b.
Ширину интерференционной полосы находим из условия:
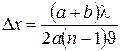 .
.
Область перекрытия волн РQ имеет протяженность (рис. 5.2.7)
х 0 = 2 b tgj » 2 b j = 2 b (n– 1)  ,
,
а максимальное число наблюдаемых полос  .
.
ОТВЕТ: 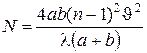 ,
, 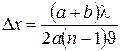 .
.
ЗАДАЧА 4. На плоскопараллельную пленку с показателем преломления
n = 1,3падает нормально параллельный пучок белого света. При какой наименьшей толщине пленки она будет наиболее прозрачна для света с длиной волны l1 = 0,60 мкм (желтый свет)? При какой наименьшей толщине пленка наиболее прозрачна одновременно для света с длинами волн l1иl2 = 0,50 мкм (голубой свет)?
| ДАНО: n = 1,3 l1 = 0,60 мкм l2 = 0,50 мкм | СИ
= 0,6·10  м
= 0,5·10 м
= 0,5·10  м м
|
 d 2 –? d 2 –?
|
АНАЛИЗ. При попадании на пленку свет частично проходит, частично отражается от поверхности пленки. Наблюдение ведется в проходящем свете. В этом случае интерферируют две волны, одна из которых проходит через пленку без отражения, вторая – испытав отражение на обеих поверхностях пленки
(рис. 5.2.8).
 Рис. 5.2.8
Рис. 5.2.8
|
Для наглядности на рис. 5.2.8 угол падения лучей не равен нулю. Результат интерференции в точке В зависит от оптической разности хода, которая в случае нормального падения лучей равна D1,2 = 2 dn.
При отражении в точках В и С изменения фазы не происходит (если показатель преломления окружающей среды больше, чем показатель преломления пленки, то изменение фазы на pпроизойдет дважды и оптическая разность хода D1,2 = 2 dn + l).
РЕШЕНИЕ. Пленка наиболее прозрачна для света с заданной длиной волны, если разность хода кратна четному числу полуволн (условие максимума):
D1,2 =2 m l / 2, где m = 1, 2, 3….
Отсюда
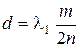 (5.2.9)
(5.2.9)
– при такой толщине пленка будет наиболее интенсивно окрашена в желтый цвет. Очевидно, наименьшая толщина пленки соответствует m = 1, т. е.  = 0,23 мкм.
= 0,23 мкм.
Одновременное максимальное прохождение желтого и голубого света означает, что толщина пленки удовлетворяет и условию (5.2.9), и условию
 , где k = 1,2… (5.2.10)
, где k = 1,2… (5.2.10)
Приравняв правые части выражений (5.2.9) и (5.2.10), получаем:
l1 / l2 = k / m.
Это значит, что наибольшая прозрачность одновременно для двух заданных длин волн возможна, если отношение этих длин волн равно отношению двух целых чисел. По условию l1/l2 = 6/5 = 12/10= и т. д.,т. е. k = 6, m = 5 – минимально возможные значения. Наименьшая толщина пленки, соответствующая этим k и m, как следует из (5.2.9) и (5.2.10), равна
d 2 = 5 l1 / (2 n)= 6l2 / (2 n) = 1,15 мкм.
Таким образом, при толщине d 2 = 1,15 z мкм, где z – любое целое число, пленка наиболее прозрачна одновременно для длин волн l1иl2. При этом
d 2 > d 1.
ОТВЕТ:  0,23 мкм, d 2 = 1,15 мкм.
0,23 мкм, d 2 = 1,15 мкм.
ЗАДАЧА 5.Плосковыпуклая стеклянная линза выпуклой поверхностью соприкасается со стеклянной пластинкой (рис. 2.2.11). Радиус кривизны выпуклой поверхности линзы R, длина волны светаl. Найти ширину D r кольца Ньютона в зависимости от его радиуса в области, где D r << r.
| ДАНО: R; l; D r << r |
| D r –? |
АНАЛИЗ. В формировании интерференционной картины участвуют пластинка, линза и тонкий воздушный клин между ними (рис. 5.2.9). В результате отражения волны от верхней и нижней граней воздушного клина происходит явление интерференции света и образуются кольца Ньютона. Необходимо определить ширину кольца, т. е. расстояние между серединами соседних темных и светлых колец.
РЕШЕНИЕ. Для расчета интерференционной картины определим оптическую разность хода лучей, отраженных от верхней и нижней граней воздушного клина:
 = 2 d + l/2,
= 2 d + l/2,
где d – толщина воздушного клина, l/2обусловлено сдвигом по фазе на p при отражении света от поверхности пластины.
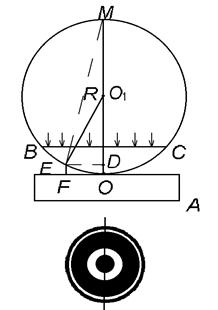 Рис. 5.2.9
Рис. 5.2.9
|
Из подобия прямоугольных треугольников ЕОD и ЕDМ следует, что  , где DО = ЕF =d, ½ DЕ ½ = rm и½ DМ ½ = 2 R– ½ EF ½ = 2 R – d » 2 R,т. к. ½ ЕF ½ << R.
, где DО = ЕF =d, ½ DЕ ½ = rm и½ DМ ½ = 2 R– ½ EF ½ = 2 R – d » 2 R,т. к. ½ ЕF ½ << R.
Таким образом, ½ EF ½ = rm 2 / 2 R, или d = rm 2 / 2 R.
Тогда
 = rm 2 / R + l/2. (5.2.11)
= rm 2 / R + l/2. (5.2.11)
Согласно условию минимума интерференции  = (2 m– 1) l/2, тогда радиус m -го темного кольца Ньютона равен
= (2 m– 1) l/2, тогда радиус m -го темного кольца Ньютона равен
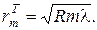
Из условия максимума  = m lc учетом выражения (5.2.11), получаем радиус m -го светлого кольца:
= m lc учетом выражения (5.2.11), получаем радиус m -го светлого кольца:
 .
.
Из этих уравнений ( )2– (
)2– ( )2 = (
)2 = ( –
–  )(
)( +
+  ) = R l/2.
) = R l/2.
Полагая rmТ + rmС » 2 r, находим ширину кольца  .
.
ОТВЕТ:  .
.