Интерференция световых волн

Интерференция это одно из явлений, где проявляются вол­новые свойства волн.

Когерентность. Рассмотрим суперпозицию двух гармониче­ских волн одинаковой частоты, которые возбуждают в интересующей нас точке пространства колебания одинакового на­правления с амплитудами А₁ и А₂. Если разность фаз этих колебаний равна , то

 

 

Рис.1.

 

возникает результирующее колебание с амплитудой А, которую легко найти с помощью векторной (или фазовой) диаграммы (рис.1) и тео­ремы косинусов:

А² = А²₁ + А²₂ + 2А₁А₂соsδ (1)

Если оба колебания не согласованы друг с другом, т. е. раз­ность фаз как-то изменяется во времени, то такие колебания называют не когерентными. В том случае, когда непрерывно изменяется, причем так, что принимает с равной вероятностью любые значения, среднее по времени значение =0, последнее слагаемое в формуле (1) обращается в ноль и остается

А² = А²₁ + А²₂

Интенсивность I пропорциональна квадрату амплитуды, поэтому

I = I₁+I₂ (2)

Это значит, что в данном случае интенсивность результирую­щего колебания равна сумме интенсивностей, создаваемых каждой из волн в отдельности.

Если же разность фаз постоянна во времени, то такие коле­бания (и волны) называют когерентными. В случае суперпозиции когерентных волн интенсивность результирующего колеба­ния, согласно (1),

I = I₁+I₂ +2 cosδ (3)

В точках пространства, где cos 8 > 0, I > I₁ + I₂; там же, где cos < О, I < I₁ + I₂. Другими словами, при суперпозиции коге­рентных волн происходит перераспределение интенсивности I в пространстве: в одних местах возникают максимумы, в других — минимумы интенсивности. Это явление называют интерферен­цией волн. Особенно отчетливо (контрастно) интерференция про­является тогда, когда I₁ = I₂. Тогда, согласно (3), I = 4 I₁ в мак­симумах и I = 0 в минимумах. Для некогерентных волн при I₁ = I₂ интенсивность I всюду одинакова и, согласно (2), I = 2I₁

Основной принцип интерференционных схем. Интерферен­ция характерна для волн любой природы и сравнительно про­сто наблюдается на опыте для волн на поверхности воды или для звуковых волн. Наблюдать же интерференцию световых волн можно лишь при определенных условиях.

Дело в том, что свет, испущенный обычными (не лазерными) источниками, не бывает монохроматическим. Ис­точники оказываются некогерентными и достаточно устойчи­вой картины интерференции не возникает. Когерентные световые волны можно полу­чить даже от обычных источников. Общий принцип их получе­ния таков: волну, излучаемую одним источником света, разде­ляют тем или иным способом на две части и затем наклады­вают их друг на друга подходящим способом.

Если разность хода этих волн от источника до точки наблю­дения не превышает некоторой характерной длины, называемой длиной когерентности, то случай­ные изменения амплитуды и фазы световых колебаний в двух волнах происходят согласованно (когерентно), и мы будем на­блюдать интерференционную картину, например систему чере­дующихся светлых и темных полос.

Образовавшиеся после разде­ления волны во всех интерференционных схемах можно пред­ставить как бы исходящими из двух точечных источников S₁ и S₂ (действительных или мнимых — это не существенно).

 

Рис.2

Рассмотрим две волны, исходящие из когерентных источни­ков S₁ и S₂ (рис. 2). В области, где эти волны перекрывают­ся, называемой зоной интерференции, возникает система чередующихся максимумов и минимумов освещенно­сти, которую можно наблюдать на экране Э.

Обозначим разность расстояний r ₂ и r ₁ от источников до ин­тересующей нас точки Р как = r ₂ - r ₁ Эту величину называ­ют разностью хода. Если разность хода равна целому числу длин волн, т. е.

= mλ, m = 0,±1, ±2,… (4)

где m — порядок интерференции, то колебания, возбуждаемые в точке Р обеими волнами, будут происходить в фазе. Таким об­разом, формула (4) есть условие возникновения интерференционных максимумов. В точках же, для которых равно полуцелому числу длин волн, образуются минимумы.

В случае, когда волны от источников распространяются не в вакууме, а в среде с показателем преломления п, в

 

 

формуле (4) под следует понимать не геометрическую, а оптическую раз­ность хода интерферирующих волн:

 

= n (r ₂ - r ₁)

 

При этом λ — это по-прежнему длина волны в вакууме.

Ширина интерференционной полосы. В практически важных случаях, угол θ «1 (см. рис.2) и разность хода можно запи­сать как

= d · ,

где d — расстояние между источниками S₂ и S₂. А так как

≈ x/l где l — расстояние от источников до экра­на, то для максимумов, согласно (4),

(5)

В точке х = 0 расположен максимум, соответствующий ну­левой разности хода. Для него порядок интерференции т = 0. Это центр интерференционной картины.

При переходе к соседнему максимуму т меняется на едини­цу и х — на величину х, которую называют шириной интер­ференционной полосы. Таким образом, x=λ / d или

 

x = λ/ψ (6)

где — угол, под которым видны оба источника из центра эк­рана, (см. рис.2).

Из этих формул видно, что для увеличения ширины полосы следует увеличивать , или уменьшать d, или то и другое, т. е. в конечном счете — уменьшать угловое расстояние ψ между ис­точниками.Размер интерференцион­ной картины обычно не превышает 1 мм, это при расстоянии от источников до экрана порядка нескольких десятков сантимет­ров.

Практически для получения более яркой интерференцион­ной картины в качестве источников S_x и S₂ используют две щели (или изображения исходного источника — щели S), и ин­терференционная картина имеет вид чередующихся светлых и темных полос, параллельных данным щелям.

 

Когерентность

Когерентностью называют согласованное проте­кание колебательных (волновых) процессов. Степень согласо­ванности называют степенью когерентности: чем лучше со­гласованность, тем выше степень когерентности.

Различают длину и ширину когерентности. В чем их суще­ство и различие мы покажем на примере первой эксперимента­льной установки для демонстрации интерференции, предло­женном Юнгом (опыт Юнга).

 

 

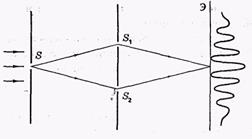
Рис.3

 

В ней яркий пучок солнечного света освещал узкую щель S (рис.3). Прошедший через щель свет вследствие дифракции образует расходящуюся волну, ко­торая падает на две узкие щели S₁ и S₂. Эти щели действуют как вторичные когерентные источники, и исходящие из них дифрагированные волны, перекрываясь, дают на экране Э сис­тему интерференционных полос.

Длина когерентности. В опыте Юнга интерференционная картина по мере удаления от ее середины размывается: неско­лько полос видны, но далее постепенно они исчезают. потому, что степень когерентности складываемых в этих точках экрана колебаний (волн) постепенно уменьшается, и колебания становятся наконец полностью некогерентными.

Длина когерентности определяется выражением

l_ког = mλ,

где m — максимальный порядок ин­терференции, соответствующий еще видимой светлой полосе.

 

 

Рис. 4

Все это можно схематически представить с помощью рис. 4: в падающей на обе щели волне (рис.3) длина когерентности _ког , щели создают две волны с той же длиной когерентности, но поскольку они достигают разных точек экрана с различными раз­ностями хода, то участки когерентности обеих волн постепенно сдвигаются относительно друг друга и, начиная с m = 5, переста­ют перекрывать друг друга — складываемые колебания стано­вятся некогерентными и интерференционные полосы исчезают.

Это справедливо при усло­вии, что «первичная» щель S достаточно узка. При расшире­нии этой щели вступает в действие другой эффект.

Найдем выражение, определяющее _ког. Известно, что строго монохроматический свет — это идеализация. Реальный свет, как бы ни стараться его монохроматизиро-вать, остается в той или иной степени немонохромати-ческим, представляющим со­бой набор монохроматических компонент в некотором конеч­ном интервале длин волн (λ,λ+ λ). Примем, что эти монохро­матические компоненты равномерно заполняют указанный интервал.

 

 

 

 

Рис.5

Как показывает формула (6), ширина полос х ~ . Изоб­разим положения максимумов для длин волн, соответствую­щих крайним значениям спектрального интервала (, + ): сплошными отрезками — для , пунктирными — для + (рис.5). Максимумы же от промежуточных длин волн запол­няют интервал между крайними максимумами каждого поряд­ка интерференции. В результате промежуточные максимумы, как видно из рисунка, будут постепенно заполнять интервал между максимумами соседних порядков для и + , А это значит, что результирующие максимумы (нижняя часть рисун­ка) будут постепенно размываться, и полосы интерференции исчезнут.

С помощью рис.5 можно заключить, что полосы исчезнут там, где т( + ) ≈ (т + 1) , здесь т — предельный порядок ин­терференции, начиная с которого полосы исчезают. Отсюда

m = / (9)

Величина / характеризует степень монохроматичности све­та: чем она больше, тем больше и степень монохроматичности.

Таким образом,, мы нашли то. значение т, при котором картина интерференции исчезает, т. е. складываемые колебания становятся уже некогерентными. Установить точное значение этого т довольно затруднительно из-за того, что
полосы размываются постепенно.

Найденное значение т (9) связано с длиной когерентности как _ког ≈ т . Отсюда следует, что

 

_ког = ²/ . (10)

 

Мы видим, что длина когерентности световой волны непо­средственно связана со степенью монохроматичности / :чем больше последняя, тем больше и длина когерентности. Для солнечного света _ког ≈ 5 , для лучших (не лазерных) источни­ков света удалось получить _ког порядка нескольких десятков сантиметров. Лазеры позволили получить излучение с _ког по­рядка сотен метров (и даже нескольких километров!).

 

 

 

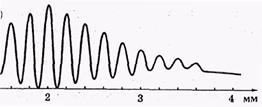
Рис.6

 

Пример. На рис.6 показана часть симметричного распределения ин­тенсивности в интерференционной картине от двух щелей (аналог опыта Юнга).

Степень монохроматично­сти, согласно (9), равна предельному порядку интерференции. Наибольшему максимуму соответствует m = 0 (третий макси­мум слева). Следующих максимумов (порядков интерферен­ции), как видно из рисунка, равно 8.Значит

Длина когерентности l_ког = mλ= 8·0,5мкм = 4мкм.

Итак, для получения интерфе­ренционной картины необходимо, чтобы оптическая разность хода складываемых колебаний была меньше длины когерент­ности: < l_ког (11)

Это требование касается всех установок, с помощью которых мы хотим наблюдать картину интерференции.

В заключение заметим, что длина когерентности связана с так называемым временем когерентности _ког — промежутком времени, в течение которого случайные изменения фазы свето­вой волны в данной точке достигают значения порядка . За это время волна распространяется на расстояние порядка _ког = с _ког.

Ширина когерентности. До сих пор щель S в опыте Юнга (рис.2) предполагалась весьма узкой (часто говорят бесконеч­но узкой). Расширение же щели, как и уменьшение степени монохроматичности света приводит к ухудшению (размытию) интерференционных полос и даже к полному их исчезновению. Чтобы выяснить роль ширины щели S, рассмотрим теперь на примере опыта Юнга другой крайний случай: излучение моно­хроматическое, щель не узкая.

Интерференционную картину на экране Э (рис.7) можно представить как наложение интерференционных картин от бес­конечно узких щелей, на которые мысленно разобьем щель S. Пусть положение максимумов на экране Э от узкой щели, взя­той около верхнего края щели S — точки 1 — таково, как отме­чено сплошными отрезками на рис.8. А максимумы от узкой щели, взятой около нижнего края щели S — точки 2 — будут смещены вверх, они отмечены пунктирными отрезками на этом же рисунке. Интервалы между этими максимумами заполнены максимумами от промежуточных узких щелей, расположен­ных между краями 1 и 2.

При расширении щели S расстояния между максимумами от ее крайних элементов будут увеличиваться, т. е. интервалы меж­ду соседними максимумами от одного края щели будут постепен­но заполняться максимумами от остальных элементов щели.

 

Рис. 7 Рис 8

Для простоты будем считать, что в схеме (рис.7) расстоя­ния а = b. Тогда при ширине щели s, равной ширине интерфе­ренционной полосы х, интервал между соседними максимума­ми от края 1 будет целиком заполнен максимумами от осталь­ных элементов щели, и интерференционные полосы исчезнут.

Итак, при расширении щели S интерференционная картина постепенно размывается и при некоторой ширине щели прак­тически исчезает.

Это наблюдаемое явление можно объяснить и иначе, а имен­но: интерференционная картина исчезает вследствие того, что вторичные источники — щели S₁ и S₂ (рис.7) становятся не­когерентными. Сказанное позволяет говорить о ширине когерен­тности падающей на щели S₁ и S₂ световой волны — ширине h_ког, на которой отдельные участки волны в достаточной степени когерентны между собой. Во избежание недоразумений уточ­ним: под шириной h_ког имеется в виду характерное для данной установки расстояние между точками поверхности, перпендику­лярной направлению распространения волны.

Найдем формулу для вычисления h_ког. В рассматриваемой схеме опыта Юнга запишем условие, при котором щели S₁ и S₂ становятся некогерентными источниками: h_ког ≈ d, где d — рас­стояние между щелями. Кроме того, мы выяснили, что интер­ференционная картина исчезает, когда ширина щели s ≈ х. Ширина же полосы х, согласно (6), равна х = λ / d. Из этих трех равенств получим: ширину когерентности

h_ког ≈ λ/φ (12)

где — угловая ширина щели S относительно диафрагмы с двумя щелями. Это значит, что ширина когерентности
пропорциональна длине волны света и об­ратно пропорциональна угловой ширине источника относительно интересующего нас места (в опыте Юнга — относитель­но места расположения двух щелей).Сказанное поясняет рис.8а.

 

Рис.8а

Если в качестве источника использовать непосредственно Солнце (его угловой размер φ ≈ 0,01 рад и λ ≈ 0,5 мкм), то ши­рина когерентности, согласно (4.12), h_ког ≈ 0,05 мм. Для полу­чения интерференционной картины от двух щелей с помощью такого излучения расстояние между двумя щелями должно быть меньше 0,05 мм, что сделать практически невозможно.

Формула (12) по существу лежит в основе метода, предло­женного Физо и осуществленного Майкельсоном — по определе­нию угловых размеров звезд путем измерения ширины когерен­тности h_ког. Попытки провести эти измерения, помещая экран с двумя щелями перед объективом телескопа оказались безуспеш­ными: полосы интерференции оставались четкими даже при наибольшем расстоянии между этими щелями. Майкельсон пре­одолел эту трудность с помощью звездного интерферометра (рис. 9). Расположенные против щелей зеркала 3₀ — 3₀ непо­движны, а зеркала 3 - 3 можно одновременно раздвигать, ме­няя расстояние h между ними. Видность полос зависит от степе­ни когерентности световых колебаний на зеркалах 3 — 3, в то время как ширина полос х определяется расстоянием между щелями. Постепенно раздвигая зеркала 3 — 3, обнаруживают, что при определенном расстоянии h между ними интерференци­онная картина исчезает. Это значит, что расстояние h между этими зеркалами оказалось ~ h_ког. Остается по формуле (12) вы­числить φ. При максимальном расстоянии h ≈ 6 м можно было измерить угловой диаметр объекта (φ ≈ 0,02 угл. сек.

 

Рис.9

 

Первой звездой, угловой диаметр которой удалось опреде­лить, была Бетельгейзе (0,047 утл. сек.). Измерив кроме того расстояние до нее (по параллаксу), определили диаметр этой звезды-гиганта (он оказался больше диаметра земной орбиты!).

Общие выводы. Для получения устойчивой интерференци­онной картины с использованием обычных (не лазерных) ис­точников света необходимо исходную световую волну расще­пить подходящим способом на две части, которые затем в обла­сти перекрытия и дадут систему полос, но... лишь в том случае, если у исходной световой волны:

1)длина когерентности _ког превышает оптическую разность хода складываемых колебаний и ширина когерентности h_ког превышает расстояние d между щелями. Можно записать:

l _ког ≥ 2 (13)

 

h _ког ≥ 2 (14)

 

Выполнение этих условий гарантирует получение интерфе­ренционной картины с достаточно хорошей видностью полос.

Рассмотрим интерференционную схему, отличаю­щуюся от схемы Юнга большей светосильностью.

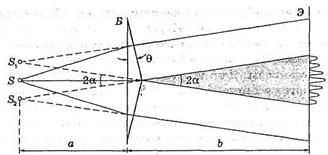Бипризма Френеля. В этой схеме для разделения исходной световой волны используют двойную призму Б (бипризму) с ма­лым преломляющим углом (рис.11).

 

Рис.11

 

Источником света слу­жит ярко освещенная узкая щель S, параллельная преломляю­щему ребру бипризмы.

Поскольку преломляющий угол бипризмы очень мал (поряд­ка десятка угловых минут), то все лучи отклоняются бипризмой на практически одинаковый угол =(n -1) , В результате образуются две когерентные волны, как бы исходящие из мнимых источников S₁и S₂, лежащих в одной плоскости со щелью S.

Ширину х интерференционных полос находим учитывая, что в данном случае = а + b и рас­стояние между изображениями S₁ и S₂ щели S равно d =a ∙2 . Таким образом,

x = (15)

 

Ширина полос тем больше, чем больше расстояние b от бипризмы до экрана.

Если же на бипризму падает плоская волна, т. е. а → ∞, то

x=λ/2a (16)

Откуда следует, что ширина полосы в этом случае не [зависит от положения экрана (расстояния b).

При наблюдении в белом свете центральный максимум (ну­левого порядка, m = 0) получается белым, остальные окрашен­ными, поскольку x~λ

Максимальное число N возможных полос интерференции на экране, где ширина зоны интерференции х = b ∙ 2 (см. рис.11), определяется условием N _макс= х/ х Отсюда следует что

N _макс= (17)

 

Необходимо учитывать роль ширины s щели (она связана с шириной когерент­ности) и степень монохроматичности λ/ λ используемого света (которая связана с длиной когерентности). Для получения интерференци­онной картины с достаточно хорошей видностью нужно, чтобы ширина s щели удовлетворяла условию

s ≤ , (18)

а степень монохроматичности — условию

≥ , (19)

где = (n -1) .

Следует обратить внимание на то, что для увеличения шири­ны х интерференционных полос нужно, согласно (15), увели­чивать отношение b/а. А чтобы использовать более широкую щель S, т. е. добиться большей светосильности установки, надо,как видно из (18.),наоборот – увеличивать обратное отношение a/b.