РАЗВИТИЕ МЕТОДОВ РАСЧЕТА ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
Метод расчета по допускаемым напряжениям
Этот метод расчета исторически сформировался первым; в нем за основу взята стадия II НДС и приняты следующие допущения:
1. напряжения в бетоне растянутой зоны принимают равными нулю;
2. бетон сжатой зоны деформируется упруго, а зависимость между напряжениями и деформациями линейная согласно закону Гука;
3. нормальные к продольной оси сечения плоские до изгиба остаются плоскими после изгиба, т.е. выполняется гипотеза плоских сечений;
4. напряжения в бетоне и арматуре ограничиваются допускаемыми напряжениями:
Рис. 5.1. К расчету балки по допускаемым напряжениям
Как следствие этих допущений, в бетоне сжатой зоны принимается треугольная эпюра напряжений и постоянное значение отношения модулей упругости материалов 
.
(5.1)
В соответствии с подобием треугольников, изображенных на рис. 5.1:
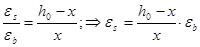(5.2)
(5.3)
Краевое напряжение в бетоне определяется как для приведенного однородного сечения:
(5.4)
Напряжения в растянутой и сжатой арматурах:
(5.5)
Момент инерции приведенного сечения равен:
(5.6)
Статический момент приведенного сечения равен нулю:
(5.7)
Напряжения в бетоне и арматуре ограничиваются допускаемыми напряжениями, которые устанавливаются как некоторые доли временного сопротивления бетона сжатию и предела текучести арматуры:
Основной недостаток метода расчета сечений по допускаемым напряжениям заключается в том, что бетон рассматривается как упругий материал. Действительное распределение напряжений в бетоне по сечению в стадии II не отвечает треугольной эпюре напряжений, а 
– число непостоянное, зависящее от значений напряжения в бетоне.
|
|
Установлено, что действительные напряжения в арматуре меньше вычисленных, т.е. имеются большие запасы, которые приводят к перерасходу материалов.
Гипотеза о предельном равновесии
В 1933 году А. Ф. Лоллейт выдвинул гипотезу предельного равновесия и отказался от кинетической гипотезы.
Постулаты гипотезы предельного равновесия:
1. Перед разрушением сечение железобетонных конструкций находится в равновесии.
2. Перед разрушением материал конструкции находится в предельном состоянии:
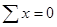
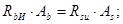(5.8)
(5.9)
– плечо внутренней пары сил.
3. Напряжения в бетоне растянутой зоны принимают равными нулю.
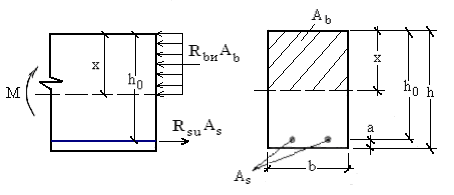
Рис. 5.2. Гипотеза о предельном равновесии
Метод расчета сечений по разрушающим усилиям
Этот метод был разработан в 1935-1938 гг.
Рис. 5.3. К расчету балки по разрушающим усилиям
Основные гипотезы:
1. Метод расчета сечений исходит из стадии III НДС при изгибе.
2. Напряжения в бетоне растянутой зоны принимают равными нулю;
3. В основу положен метод предельного равновесия.
4. В расчетные формулы вместо допускаемых напряжений вводят предел прочности бетона при сжатии и предел текучести арматуры.
Расчетное сопротивление бетона сжатию принято:
§ для изгибаемого элемента 
;
§ сопротивление бетона сжатию (призменная прочность) – 
;
§ сопротивление растяжению арматуры равно физическому пределу текучести 
= 
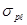, либо условному пределу текучести = 
.
Эпюра напряжений в бетоне сжатой зоны вначале принималась криволинейной, а затем была принята прямоугольной.
|
|
Для изгибаемого элемента с любым симметричной формы сечением высоту сжатой зоны определяют из уравнения (5.8) равновесия внутренних усилий в стадии разрушения. Разрушающий момент определяют как момент внутренних усилий относительно оси, проходящей через цент тяжести растянутой арматуры (уравнение (5.9)).
Для прямоугольных и тавровых сечений с полкой в сжатой зоне граничное значение высоты сжатой зоны принимают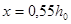 
.
На практике нужны менее жесткие условия, тогда вместо уравнения (5.9) можно записать условие:
где 
– статический момент инерции;
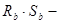несущая способность железобетонной конструкции, зависящая от геометрических размеров и прочности материала.
При расчете этим методом в формулах учитывают запас прочности – единый для элемента в целом. Коэффициент запаса прочности 
был установлен нормами в зависимости от причины разрушения конструкции, сочетания силовых воздействий и отношения усилий от временных нагрузок к усилиям от постоянных нагрузок.
где 
.
В расчетах сечений по разрушающим усилиям внутренние усилия M, Q, N от нагрузки определяют также в стадии разрушения конструкции, т.е. с учетом образования пластических шарниров. Для многих видов конструкций – плит, неразрезных балок, рам – такого рода расчеты дают существенный экономический эффект.
Достоинства метода расчета:
Данный метод, учитывающий упругопластические свойства железобетона, более правильно отражает действительную работу сечений конструкций под нагрузкой и является серьезным развитием в теории сопротивления железобетона. Большим преимуществом этого метода является возможность определения близкого к действительности общего коэффициента запаса прочности. При расчете по разрушающим усилиям в ряде случаев получается меньший расход арматурной стали по сравнению с расходом стали по методу допускаемых напряжений.
|
|
Недостатки метода расчета:
1. Не охвачена жесткость и трещиностойкость конструкций.
2. Коэффициент запаса складывается из разных коэффициентов
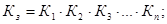
где 
коэффициент по нагрузкам и воздействиям;
коэффициент по прочности бетона и т.д.
Возможные отклонения фактических нагрузок и прочностных характеристик материалов от их расчетных значений не могут быть явно учтены при одном общем синтезирующем коэффициенте запаса прочности. При необходимой замене какого-нибудь 
, приходится менять все коэффициенты, составляющие коэффициент запаса 
.
Метод расчета сечений по предельным состояниям
Метод расчета конструкций по предельным состояниям является дальнейшим развитием метода расчета по разрушающим усилиям. При расчете по этому методу устанавливают предельные состояния конструкций и используют систему расчетных коэффициентов, введение которых гарантирует, что такое состояние не наступит при самых неблагоприятных сочетаниях нагрузок и при наименьших значениях прочностных характеристик материалов. Прочность сечений определяют по стадии разрушения, но безопасность работы конструкции под нагрузкой оценивают не одним синтезирующим коэффициентом запаса, а указанной системой расчетных коэффициентов. Конструкции, запроектированные и рассчитанные по данному методу, получаются несколько экономичнее.
Выделяли 3 группы предельных состояний:
1. по несущей способности:
2. по деформативности;
3. по трещиностойкости.
Затем последние 2 группы объединили в единую группу – группу по условиям эксплуатации.
При расчете по предельным состояниям используют не сопротивление сжатию при изгибе 
как в методе по разрушающим усилиям, а призменную прочность .
Предельное состояние – это состояние конструкции, при наступлении которого конструкция перестает удовлетворять предъявленным к ней требованиям, т.е. теряет способность сопротивляться внешним нагрузкам и воздействиям или получает недопустимые значения деформаций или трещиностойкости.
Оценка недопустимых деформаций определяется с помощью прогибов или углов поворота.
Расчет по предельным состояниям первой группы выполняют, чтобы обеспечить прочность, устойчивость, выносливость конструкций.
Расчет по предельным состояниям второй группы выполняют для избежания образования и чрезмерного раскрытия трещин (если те предусмотрены по условиям эксплуатации), а также чрезмерных перемещений (прогибов, углов поворота).
Расчет по предельным состояниям конструкции в целом, а также отдельных ее элементов или частей выполняют для всех этапов: изготовления, транспортирования, монтажа и эксплуатации. При этом расчетные схемы должны отвечать принятым конструктивным решениям и каждому из перечисленных этапов.
Между 2 группами предельных состояний есть качественная разница:
- 1 группа защищает от обрушения;
- 2 группа отвечает за комфортность эксплуатации.
Рис. 5.4. Пример конструкции, не отвечающей требованиям
Нормальной эксплуатации
Существуют некоторые ограничения для 2 группы – ограничения по деформациям:
1. конструктивные – прогибы должны быть такими, чтобы не мешать эксплуатации других конструкций;
2. технологические – прогибы должны быть такими, чтобы не мешать работе технологического оборудования;
3. эстетические – прогибы должны быть такими, чтобы не мешать комфортности людей.