МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ МНОЖЕСТВ

ТАБЛИЦЫИСТИННОСТИ И ПОРЯДОК ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ

Для логических операций приняты следующие обозначения:

A, A	не A (отрицание, инверсия)
A ∧ B, A ⋅ B	A и B (логическое умножение, конъюнкция)
A ∨ B, A + B	A или B (логическое сложение, дизъюнкция)
A → B	импликация (следование)
A ↔ B, A ≡ B, A ∼ B	эквиваленция (эквивалентность, равносильность)
A ⊕ B	сложение по модулю 2 (XOR)

 

Отрицание (НЕ):

Таблица истинности операции НЕ

Конъюнкция (И):

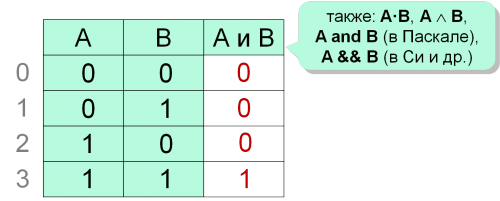
Таблица истинности операции И (конъюнкция)

Дизъюнкция (ИЛИ):

Таблица истинности операции ИЛИ (дизъюнкция)

Импликация (если…, то…):

Таблица истинности операции Импликация (если…, то…)

Эквивалентность (тогда и только тогда, …):

Таблица истинности операции Эквивалентность (тогда и только тогда, …)

Сложение по модулю 2 (XOR):

A	B	A ⊕ B

Порядок выполнения операций:

· если нет скобок, сначала выполняются все операции «НЕ », затем – «И », затем – «ИЛИ », импликация, равносильность

Еще о логических операциях:

· логическое произведение X∙Y∙Z∙ … равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)

· логическая сумма X+Y+Z+ … равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)

 

Преобразование логических операций

· операцию импликация можно преобразовать в операции ИЛИ и НЕ:

A → B = A ∨ B
или
A → B = A + B

· операцию эквивалентность можно преобразовать:

A ↔ B = A ⊕ B = A ∧ B ∨ A ∧ B
или
A ↔ B = A ⊕ B = A · B + A · B

· операцию XOR (сложение по модулю 2) можно преобразовать так:

A ⊕ B = (A ∧ B) ∨ (A ∧ B)
или
A ⊕ B = (A · B) + (A · B)

Законы алгебры логики:

· кроме того, могут пригодиться формулы:

Закон двойного отрицания:

A = A

Закон исключения третьего:

A ∧ A = 0 или A · A = 0
A ∨ A = 1 или A + A = 1

Закон повторения (идемпотентности):

A ∧ A = A или A · A = A
A ∨ A = A или A + A = A

Законы исключения логических констант:

A ∧ 0 = 0
A ∧ 1 = A
A ∨ 0 = A
A ∨ 1 = 1

Переместительный (коммутативный) закон:

A ∧ B = B ∧ A
A ∨ B = B ∨ A

Сочетательный (ассоциативный) закон:

(A ∧ B) ∧ C = A ∧ (B ∧ C)
(A ∨ B) ∨ С = A ∨ (B ∨ С)

Распределительный (дистрибутивный) закон:

(A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C)
(A ∨ B) ∧ С = (A ∧ С) ∨ (B ∧ С)
и наоборот:
(A ∨ B) ∧ (A ∨ C) = A ∨ (B ∧ C)
(A ∧ B) ∨ (A ∧ C) = A ∧ (B ∨ C)

Закон общей инверсии (Законы де Моргана):

(A ∧ B) = A ∨ B
(A ∨ B) = A ∧ B

· упрощать выражения можно с помощью формул:

Закон поглощения:

A ∨ A ∧ B = A
A ∧ (A ∨ B) = A
A ∨ A ∧ B = A ∨ B

· Порядок выполнения логических операций:

1. выражения в скобках,

2. операции «НЕ»,

3. операции «И»,

4. операции «ИЛИ»,

5. операции «импликация»

6. операции «эквиваленция»

· последовательность из операций импликации выполняется слева направо (при этом соблюдается принцип «операции с одинаковым приоритетом выполняются слева направо»):

A → B → C → D = ((A → B) → C) → D

МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ МНОЖЕСТВ

· пересечение множеств соответствует логическому умножению, а объединение – логическому сложению;

· пересечением двух множеств называется новое множество, состоящее из элементов, принадлежащих одновременно обеим множествам:

Пример:

· объединением двух множеств называется новое множество, состоящее из элементов, принадлежащих отдельно каждому из множеств (без повторений);

Пример:

· пустое множество ∅ – это множество, в котором не содержится ни одного элемента; пустому множеству в теории множеств соответствует 0;

· универсальное множество U (на кругах Эйлера обозначается в виде прямоугольника) – это множество, содержащее все возможные элементы определенного типа (например, все вещественные числа):

· универсальное множество соответствует логической единице: для любого множества целых чисел X справедливы равенства:

X ∨ U = U и X ∧ U = X

· разностью двух множеств A и B называется новое множество, элементы которого принадлежат A, но не принадлежат B:

Пример разности множеств:

· дополнение множества X – это разность между универсальным множеством U и множеством X (например, для целых чисел X – все целые числа, не входящие в X)

· пусть требуется выбрать множество A так, чтобы выполнялось равенство A ∨ X = I; в этом случае множество A должно включать дополнение X, то есть A ≥ X (или A ⊇ X), то есть A_min = X

· пусть требуется выбрать множество A так, чтобы выполнялось равенство A ∨ X = I, в этом случае множество A должно включать дополнение X, то есть A ⊇ X; отсюда A ⊆ X, то есть A_max = X

Для большей определенности стоит рассмотреть тему круги Эйлера.