Решение различных краевых задач неустановившейся фильтрации упругой жидкости в упругой пористой среде в условиях как бесконечного, так и конечного пластов часто представляются громоздкими формулами в виде бесконечного медленно сходящегося ряда или несобственного интеграла, содержащего специальные функции. В связи с этим были предприняты поиски приближенных эффективных решений задач неустановившейся фильтрации. Отметим лишь характерные особенности некоторых из разработанных приближенных методов, применяемых при решении задач упругого режима.
Метод последовательной смены стационарных состояний (ПССС)
Одним из наиболее простых по идее приближенных методов решения задач неустановившейся фильтрации является метод последовательной смены стационарных состояний (ПССС), развитый И.А. Чарным и широко применяемый в практических расчетах. Метод основан на предположении, что давление в пласте изменяется во времени значительно медленнее, чем по координатам. Поэтому в основном уравнении упругого режима фильтрации (7.10) производную по времени можно в первом приближении отбросить, в результате чего для давления получается уравнение Лапласа, описывающее стационарный процесс. В этом случае в каждый момент времени вся область движения жидкости, в действительности охватывающая весь пласт, условно разделяется на две области: возмущенную и невозмущенную. При этом предполагается, что в возмущенной области, начинающейся от стенки скважины, давление распространяется так, как будто бы движение жидкости в ней установившееся; внешняя граница этой области служит контуром питания.
В невозмущенной области пласта давление всюду постоянно и равно начальному статическому. Закон движения подвижной границы раздела возмущенной и невозмущенной областей определяется при помощи уравнения материального баланса и граничных условий.
Рассмотрим схематично применение метода ПССС для случаев плоскопараллельного и плоскорадиального потоков упругой жидкости.
Прямолинейно-параллельный фильтрационный поток.
Рассмотрим полубесконечный горизонтальный пласт во всей области которого первоначально существовало постоянное давление Рк. В начальный момент времени (t=0) в сечении Х=0 пласта толщиной h и шириной В давление внезапно снизилось и стало равным Рг= const. К некоторому моменту времени t>0 после пуска галереи граница возмущенной области распространилась на длину 
. (Рис.51).
Рис.51
Распределение давления в возмущенной зоне принимается установившимся
, (7.52)
т.е. эпюра давлений Р(x) представляет собой прямую линию, перемещающуюся вдоль пласта с угловой точкой x= . Заметим, что в точном решении этой задачи эпюра давлений угловой точки не имеет.
Рассматривая массу жидкости, отобранной за счет ее упругости из возмущенной области пласта 
, ее массовый расход, выраженный по закону Дарси, получаем дифференциальное уравнение для границы 
возмущенной зоны пласта, интегрирование которого дает закон движения этой границы:
. (7.53)
Тогда закон распределения давления в возмущенной зоне пласта (7.52) принимает вид
,
или
; (7.54)
где 0 < x £ 2 
;
а при x > 
, 
.
Нетрудно определить дебит галереи:
. (7.55)
Погрешность расчета дебита галереи по приближенной формуле (7.55) по сравнению с расчетами по точной формуле (7.24) не превосходит 11%.
Плоскорадиальный фильтрационный поток.
Рассмотрим плоскорадиальный приток упругой жидкости к скважине радиуса rc из неограниченного горизонтального пласта постоянной толщины h (рис.52); скважина работает с постоянным дебитом Q; первоначально давление во всем пласте было одинаковым и равным Рк.
Рис. 52
После пуска скважины в работу вокруг нее образуется воронка депрессии, которая теоретически охватывает весь пласт. Приближение в решении задачи заключается в том, что мы последовательно во времени фиксируем радиус воронки депрессии, т.е. в каждый момент времени радиус воронки R(t) принимается как конечная величина. При этом кривая распределения давления аппроксимируется логарифмической кривой, т.е.
. (7.56)
При этом дебит скважины будет описываться формулой, аналогичной формуле Дюпюи:
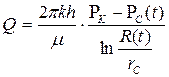. (7.57)
Размер возмущенной области R(t) также находится из рассмотрения уравнения материального баланса для упругой жидкости, отобранной из этой области пласта. В итоге закон движения границы R(t) возмущенной зоны пласта имеет вид:
. (7.58)
Тогда из равенства (7.56) находится давление в любой точке пласта в любой момент времени t:
, (7.59)
где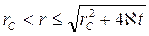 
,
а при 
Депрессия на скважине (r = rC) в момент t будет:
(7.60)
Сравнивая (7.60) с депрессией, определенной по точной формуле (7.39), убеждаемся, что относительная погрешность уменьшается с течением времени и составляет:
10,6 %, если 
;
7,5 %, если 
;
5,7 %, если 
.
Метод А.М. Пирвердяна
Этот метод аналогичен методу ПССС и уточняет его. В методе А.М. Пирвердяна, как и в методе ПССС неустановившийся фильтрационный поток в каждый момент времени мысленно разбивается на две области – возмущенную и невозмущенную. Граница между этими областями также определяется из уравнения материального баланса. Но в отличие от метода ПССС распределение давления в возмущенной области по методу А.М.Пирвердяна задается в виде квадратичной параболы так, чтобы пьезометрическая кривая по границе областей касалась горизонтальной линии, представляющей давление в невозмущенной области. Распределение давления уже не будет стационарным, а градиент давления по границе областей становится равным нулю, что обеспечивает плавное смыкание профиля давлений в возмущенной и невозмущенной областях.
 |
Рис. 53
Рассмотрим прямолинейно-параллельный фильтрационный поток упругой жидкости (рис.53). В горизонтальном пласте постоянной толщины h и ширины B пущена в эксплуатацию галерея с постоянным дебитом Q. К моменту времени t после пуска граница возмущенной области продвигается на величину 
, при этом кривая распределения давления в этой области задается в виде параболы так, что в точке 
касательная к параболе горизонтальна, т.е.
(7.61)
Дебит галереи определяется по закону Дарси
. (7.62)
Учитывая (7.61), находим выражение для дебита галереи
. (7.63)
Закон движения внешней границы возмущенной области определяется из уравнения материального баланса (как и при методе ПССС) и имеет вид:
. (7.64)
Распределение давления (7.61) в возмущенной области пласта с учетом (7.63) и (7.64) принимает вид
, (7.65)
где 
;
при 
.
Расчет депрессии 
по формуле (7.65) дает погрешность по сравнению с точным решением примерно 9%, т.е. в 2,5 раза меньше, чем метод ПССС.
Аналогичным образом строится решение и для случая плоскорадиального потока. В этом случае распределение давления в возмущенной области пласта задается в виде
, (7.66)
где R(t) - радиус внешней границы возмущенной области пласта.
Заметим, что отбросив последнее слагаемое в уравнении (7.66), получаем закон распределения давления при методе ПССС.