VII. НЕУСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ УПРУГОЙ ЖИДКОСТИ В УПРУГОЙ ПОРИСТОЙ СРЕДЕ
Упругий режим пласта и его характерные особенности
В практике разработки и эксплуатации нефтяных и газовых месторождений в пластах часто возникают неустановившиеся процессы, связанные с пуском или остановкой скважины, с изменением темпов отбора флюида из скважины. Характер этих процессов проявляется в перераспределении пластового давления, в изменениях во времени скоростей фильтрационных потоков, дебитов скважин и т.д.
Особенности этих процессов зависят от упругих свойств пластов и насыщающих их жидкостей, т.е. основным видом пластовой энергии в этих процессах является энергия упругой деформации жидкостей (нефти и воды) и материала пласта (горной породы). При этом предполагается, что фильтрационный поток однофазный, т.е. давление в любой точке потока выше давления насыщения.
При снижении пластового давления объем сжатой жидкости увеличивается, а объем порового пространства сокращается за счет расширения материала пласта. Все это способствует вытеснению жидкости из пласта в скважину.
Хотя коэффициенты объемной упругой деформации жидкости и горной породы малы, но зато очень велики бывают объемы пласта и насыщающих их жидкостей, поэтому объемы жидкости, извлекаемой из пласта за счет упругости пласта и жидкости, могут быть весьма значительными.
Характерная особенность проявления упругого режима в процессе разработки нефтяных месторождений – длительность процесса перераспределения пластового давления после начала работы скважины или изменения темпа отбора жидкости из скважины. Это связано с тем, что при фильтрации вязкой жидкости в пласте возникают очень большие силы сопротивления. Неустановившиеся процессы протекают тем быстрее, чем больше коэффициент проницаемости пласта К, и тем медленнее, чем больше коэффициент вязкости жидкости m и коэффициенты объемной упругости жидкости bЖ и пласта (среды) bС.
|
|
Теория упругого режима была начата работами Стрижова И.Н., М. Маскета, Р.Шилсюиза, У.Херста. Однако наиболее строго основы теории упругого режима были разработаны в нашей стране В.Н Щелкачевым. Им были впервые учтены влияние объемной упругости пористой среды и впервые решены фундаментальные задачи теории упругого режима для практических целей разработки нефтяных месторождений.
Обратимся к общему дифференциальному уравнению (6.8) неустановившегося движения сжимаемой жидкости по закону Дарси в деформируемой пористой среде; при этом принимаем k=const и m=const, т.е.
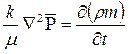, (7.1)
где
- функция Лейбензона (7.2)
Используя уравнения состояния упругой жидкости (2.9) и упругой пористой среды (2.23)
;
,
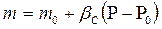находим произведение (mr) для (7.1)
.
Последним слагаемым (ввиду его малости по сравнению с первыми слагаемыми) пренебрегаем.
Получаем
,
или
.
Обозначим 
(7.3)
и называем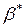 
- коэффициентом упругоемкости пласта.
Тогда
.
Дифференцируя по времени, находим
. (7.4)
В свою очередь функция Лейбензона (7.2) принимает вид (6.15) с учетом (2.9)
,
т.е.
. (7.5)
Дифференцируя (7.5) дважды по координатам и складывая, получим
. (7.8)
Подставляя (7.4) и (7.8) в исходное диф. уравнение (7.1), будем иметь
,
или
.
Обозначим
, (7.9)
тогда окончательно получим
|
|
;
т.е.
. (7.10)
Уравнение (7.10) является основным дифференциальным уравнением упругого режима фильтрации.
Уравнение вида (7.10) в математической физике известно под названием уравнения теплопроводности. По аналогии с коэффициентом температуропроводности, который характеризует скорость перераспределения температуры в проводниках, коэффициент 
в теории упругого режима назван В.Н.Щелкачевым коэффициентом пьезопроводности, характеризующий скорость перераспределения давления в пласте.
Размерность 
можно установить из (7.9)
,
где L,M,T – соответственно размерность длины, массы и времени.
Наиболее встречающиеся в нефтепромысловой практике значения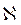 
=(0,1¸5) м2/с.
Уравнение (7.10) позволяет решать ряд задач неустановившегося движения жидкости при упругом режиме. В частности при соответствующих начальных и граничных условиях находится закон распределения давления в пласте Р=Р(x,y,z,t).