VIII. НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ГАЗА В ПОРИСТОЙ СРЕДЕ
Теория движения газа в пористой среде была разработана Л.С. Лейбензоном. Он получил дифференциальное уравнение для определения давления в пласте при неустановившемся движении в нем идеального газа. Б.Б.Лапук в работах, посвященных основам разработки месторождений природных газов, показал в частности, что неустановившуюся фильтрацию газа можно рассматривать как изотермическую, так как изменения температуры газа, возникающие при изменении давления, в значительной мере компенсируются теплообменом со скелетом пористой среды.
Для вывода дифференциального уравнения неустановившейся фильтрации идеального газа подставим в уравнение неразрывности (2.2)


выражения (2.1) для компонент скорости фильтрации
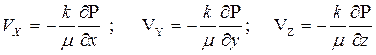
и уравнения состояния (плотности) идеального газа (2.14)
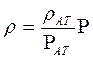 .
.
Считая коэффициенты пористости m0, проницаемости k и вязкости m газа постоянными, из уравнения (2.2) на основании (2.1) и (2.14) получим
 . (8.1)
. (8.1)
Выражения в скобках в левой части уравнения (8.1) можно представить следующим образом:
 ,
,
тогда уравнение (8.1) примет вид
 . (8.2)
. (8.2)
Выражение в скобках представляет собой оператор Лапласа относительно Р2, поэтому уравнение (8.2) можно кратко записать в виде
 . (8.3)
. (8.3)
Полученное дифференциальное уравнение (8.3) неустановившейся фильтрации газа называется уравнением Лейбензона и представляет собой нелинейное уравнение параболического типа. Заметим, что оно справедливо для идеального газа при выполнении закона Дарси. Изменением пористости пренебрегают, потому что оно входит в уравнение неразрывности (2.2) в виде произведения (rm), в котором плотность газа изменяется в гораздо большей степени, чем пористость.
Уравнение Лейбензона (8.3) можно записать иначе, умножив правую и левую части на давление Р и заменив  ;
;
получаем  . (8.4)
. (8.4)
Для решения конкретных задач, связанных с неустановившейся фильтрацией газа, дифференциальное уравнение в форме (8.3) или в форме (8.4) должно быть проинтегрировано по всей газовой залежи при заданных начальных и граничных условиях. Но поскольку уравнение (8.3) или (8.4) представляет собой сложное нелинейное уравнение в частных производных, то оно неимеет точных аналитических решений даже в самых простых одномерных случаях. Его можно проинтегрировать численно с помощью ЭВМ или решить приближенным способом. Приближенные способы хорошо разработаны (например, метод ПССС).
Неустановившаяся фильтрация реального газа с уравнением состояния
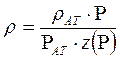
и с учетом зависимости m = m (Р) в недеформируемой пористой среде (m0 = const; k = const) описывается следующим нелинейным дифференциальным уравнением параболического типа:
 .
.
(8.5)
Это уравнение можно проинтегрировать численным методом на ЭВМ или решить приближенно при помощи электрических моделей.
2. Линеаризация уравнения Лейбензона и основное решение линеаризованного уравнения
Если заменить нелинейное дифференциальное уравнение (8.4) линейным, т.е линеаризовать его, то оно упростится – для линейного уравнения существуют точные аналитические решения. Ясно, что точные решения линейного уравнения будут приближенными решениями для нелинейного уравнения. Оценить погрешность такого приближенного решения уравнения (8.4) можно, сравнивая приближенное решение с решением этого уравнения (8.4) на ЭВМ.
Известны различные способы линеаризации основного дифференциального уравнения (8.4). Если рассматривается плоскорадиальный приток к скважине, то как известно из теории стационарной фильтрации газа, воронка депрессии очень крутая и по большей части пласта давление Р(r) мало отличается от контурного РК. На этом основании Лейбензон предложил заменить переменное давление Р в коэффициенте (правая часть) уравнения (8.4) на постоянное давление РК (начальное давление в пласте),т.е.
 .
.
Тогда вместо уравнения (8.4) получим уравнение
 , (8.5)
, (8.5)
которое является линейным уравнением пьезопроводности относительно функции Р2.
И.А.Чарный предложил свести уравнение (8.4) к линейному заменой переменного давления Р в коэффициенте À на 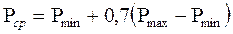 ,
,
где  - максимальное и минимальное давление в газовой залежи за расчетный период эксплуатации.
- максимальное и минимальное давление в газовой залежи за расчетный период эксплуатации.
Рассмотрим конкретно задачу о притоке газа в скважину бесконечно малого радиуса (точечный сток), расположенной в пласте бесконечной протяженности с постоянной толщиной h. В начальный момент времени пласт невозмущен, т.е. при t = 0 давление во всем пласте постоянно и равно РК. Надо найти изменение давления в пласте с течением времени – Р(r,t), если отбор газа происходит с постоянным дебитом: QАТ = const.
Для решения этой задачи используем линеаризованное уравнение (8.5), которое для плоскорадиальной фильтрации запишется следующим образом:
 . (8.6)
. (8.6)
Уравнение (8.6) надо проинтегрировать
при начальном условии
при  (8.7)
(8.7)
при граничном условии в отдаленных точках
при 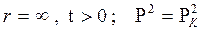 . (8.8)
. (8.8)
Выведем условие для давления на забое скважины. Для этого, исходя из закона Дарси, напишем выражение для массового дебита в дифференциальной форме для плоскорадиальной фильтрации.
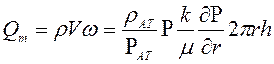 .
.
Используя равенства  и разделив на rАТ, получим
и разделив на rАТ, получим
 . (8.9)
. (8.9)
Из этого соотношения выразим условие на стенке скважины бесконечно малого радиуса
 . (8.10)
. (8.10)
Таким образом, для решения поставленной задачи уравнение (8.6) должно быть проинтегрировано при условиях (8.7), (8.8) и (8.10).
Ранее была рассмотрена аналогичная задача об отборе упругой жидкости с постоянным дебитом Q из бесконечного первоначально невозмущенного пласта; эта задача была представлена уравнением (7.25) с условиями (7.26) и (7.27).
Нетрудно видеть аналогию рассматриваемой задачи с задачей неустановившейся фильтрации упругой жидкости: во все соотношения для идеального газа давление входит в квадрате; коэффициент пьезопроводности жидкости  заменяется на
заменяется на 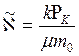 для газа; коэффициент
для газа; коэффициент  - на
- на  . В остальном все соотношения аналогичны. Поэтому и решение данной задачи можно записать сразу по аналогии с упругой жидкостью:
. В остальном все соотношения аналогичны. Поэтому и решение данной задачи можно записать сразу по аналогии с упругой жидкостью:
 , (8.11)
, (8.11)
или
 . (8.12)
. (8.12)
Для малых значений аргумента  в соответствии с формулой (7.43) можно заменить интегральную показательную функцию логарифмической:
в соответствии с формулой (7.43) можно заменить интегральную показательную функцию логарифмической:
 , (8.13)
, (8.13)
или
 . (8.14)
. (8.14)
Подчеркнем, что решения (8.11) – (8.14) являются приближенными, поскольку получены в результате интегрирования линеаризованного уравнения (8.6), а не точного (8.2). Формулы (8.12) и (8.14), определяющие распределение давления вокруг газовой скважины с момента t = 0 при Q = const, дают кривые, идентичные кривым при установившейся фильтрации - они очень круты вблизи скважины (рис.53).
По заданному r можно найти давление Р в любой момент времени t по формуле (8.12) или (8.14).

Рис. 53
В частности (на скважине).
 .
.
Численное решение дифференциального уравнения (8.2) показывает, что погрешность в решении линеаризованного уравнения (8.5) составляет доли процента.
3. Решение задачи о притоке газа к скважине методом последовательной смены стационарных состояний
Отметим, что метод ПССС основан на следующих предпосылках:
1) в каждый момент времени существует конечная возмущенная область, в которой происходит движение газа к скважине;
2) движение газа внутри возмущенной области стационарно;
3) размер возмущенной области определяется из уравнения материального баланса.
Рассмотрим решение задачи (методом ПССС) о притоке газа к скважине с постоянным дебитом QАТ; радиус скважины rC.
В любой момент времени возмущенной областью является круговая область радиусом R (t), внутри которой давление распределяется по стационарному закону (6.26)
 ,
,  . (8.15)
. (8.15)
Вне возмущенной области давление равно начальному (невозмущенное состояние):
Р = РК, r > R (t). (8.16)
Для возмущенной зоны можно записать выражение дебита по формуле (6.28) для стационарной фильтрации:
 , (8.17)
, (8.17)
Заметим, что в нашей задаче (при QАТ = const) забойное давление РС = РС (t).
Для дальнейших выводов выделим из (8.17) отношение:
 .
.
и подставим в формулу (8.15). Получим:
 . (8.18)
. (8.18)
Для нахождение R (t) составим уравнение материального баланса.
Начальный запас газа (при Р = РК) в зоне пласта радиусом R (t)
 . (8.19)
. (8.19)
Текущий запас газа выразим через средневзвешенное давление  :
:
 , (8.20)
, (8.20)
где  определяется по формуле (6.30) установившейся фильтрации
определяется по формуле (6.30) установившейся фильтрации
 (8.21)
(8.21)
Так как отбор происходит с постоянным дебитом QАТ, то отобранная масса газа к моменту t равна  . Следовательно
. Следовательно
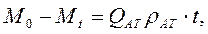
или с учетом (8.19) и (8.20), имеем
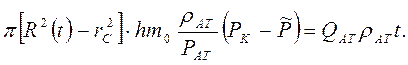 (8.22)
(8.22)
Подставляя в (8.22) выражения (8.21) для  и (8.17) для QАТ, получим
и (8.17) для QАТ, получим

откуда 
или 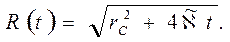 (8.23)
(8.23)
Для значений времени, для которых  имеем
имеем
 . (8.24)
. (8.24)
Зная закон движения границы возмущенной области в виде (8.23) или (8.24), можно найти давление в любой точке возмущенной зоны пласта и на забое скважины по формуле (8.18)
 (8.25)
(8.25)
 ;
;
 (8.26)
(8.26)
Формула (8.25) и (8.26) пригодны как для бесконечного пласта, так и для конечного открытого или закрытого пластов радиусом  . В последнем случае они годятся только для первой фазы движения, пока воронка депрессии не достигнет границы пласта, т.е. для
. В последнем случае они годятся только для первой фазы движения, пока воронка депрессии не достигнет границы пласта, т.е. для  .
.
Изменение давления во второй фазе зависит от типа газового пласта. Если он закрыт, то давление будет продолжать снижаться во всем пласте, включая границу.
Если он открытый (Р = РК при r = RK), т.е. режим водонапорный, то во второй фазе установится стационарный режим с постоянной депрессией
(РК - РС), где
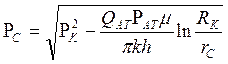 . (8.27)
. (8.27)