Использование Mathcad для решения обыкновенного дифференциального уравнения.

Кафедра технической кибернетики

Численные методы и оптимизация

Лабораторная работа № 6.

Численное решение обыкновенных дифференциальных уравнений.

Вариант № 1

Выполнил: студент группы УС‑21 Шифр группы Локтев Т. Н. ФИО 17.05.2019 Подпись Дата		Принял: ст. преп. кафедры ТК Должность — Ученая степень, звание Рыбин И. А. ФИО
Замечания:		Отметка о выполнении: Подпись Дата Отметка о защите: Подпись Дата

 

Содержание

1. Постановка задачи........................................................................................... 3

2. Аналитическое решение................................................................................... 4

3. Численное решение............................................................................................ 5

3.1. Метод Эйлера.......................................................................................... 5

3.2. Уточнённый метод Эйлера..................................................................... 6

3.3. Метод Рунге-Кутта................................................................................ 7

3.4. Метод Адамса.......................................................................................... 8

3.5. Метод Милна........................................................................................... 9

4. Использование Mathcad для решения обыкновенного дифференциального уравнения............................................................................................................. 11

5. Программная реализация............................................................................... 13

5.1. Интерфейс и функционал программы................................................... 13

5.2. Описание основных подпрограмм, типов данных и переменных....... 13

6. Результаты работы и основные выводы....................................................... 14

Приложение А. Текст программы................................................................. 15

 

Постановка задачи

Постановка задачи

Необходимо решить дифференциальное уравнение с начальным условием 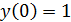на отрезке интегрирования [0; 0,5] методом:

1) Эйлера;

2) Уточнённым Эйлера;

3) Рунге - Кутта (4–го порядка);

4) Адамса;

5) Милна.

 

Аналитическое решение

, .

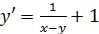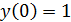Для решения данного уравнения введем замену . Затем продифференцируем её по 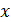и выполним преобразования:

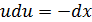
Интегрируем:

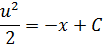
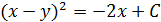
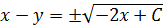
Подставим значения 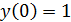для нахождения коэффициента :

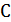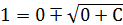
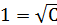
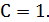
Следовательно, точное решение 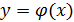имеет вид: ,
при

 

 

Численное решение

Метод Эйлера

На каждом частичном интервале [ ] заменим интегральную кривую прямой, проходящей через точки [ 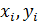] соответственно и имеющими угловой коэффициент :

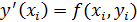при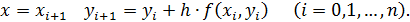

Вместо дифференциального решается нелинейное разностное уравнение: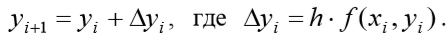

Зададимся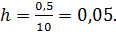

Представим полученное решение в таблице 1.

Таблица 1

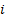
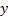
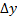
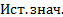
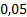
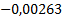
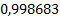
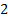
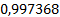
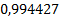
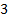
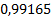
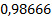
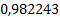
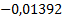
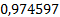
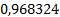
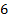
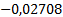
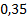
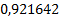
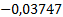
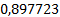
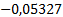
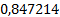
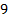
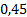
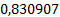
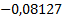
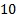
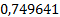
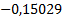
Геометрическая интерпретация данного метода выглядит следующим образом (Рис. 1):

Рис. 1. Геометрическая интерпретация метода Эйлера

 

Уточнённый метод Эйлера

Подынтегральная функция заменяется значением в точке .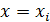

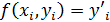Тогда

Определим 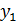, как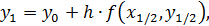

где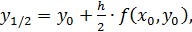

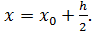
Возьмем

Вычисления по данному методу представим в таблице 2.

Таблица 2

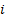
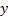
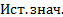
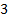
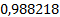
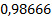
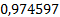
Геометрическая интерпретация данного метода выглядит следующим образом (Рис. 2):

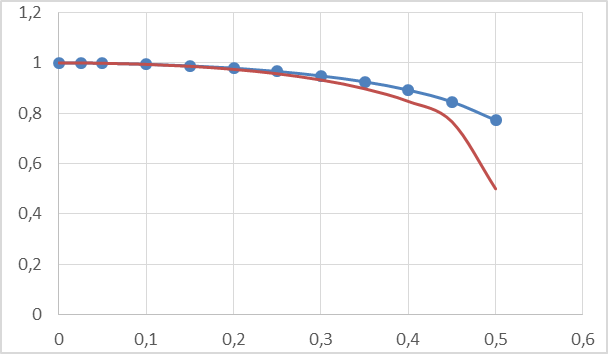
Рис. 2. Геометрическая интерпретация уточненного метода Эйлера

 

Метод Рунге-Кутта

Решение уравнения по данному методу заключается в выполнении последовательных операций, которые включают в себя вычисления вспомогательных функций :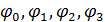

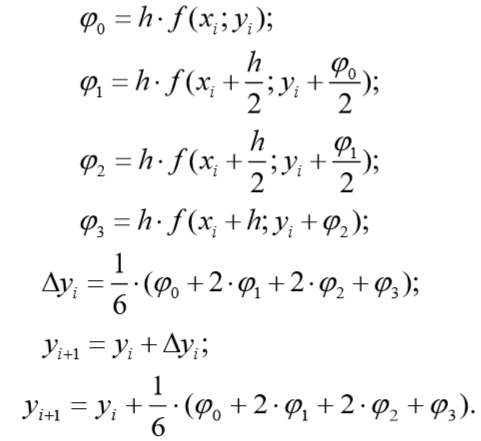
Полученные вычисления представим в таблице 3.

Таблица 3

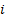
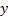
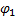
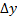
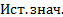
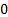
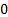
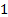
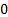
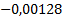
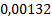
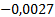
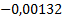
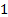
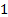
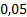
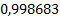
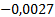
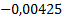
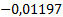
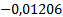
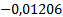
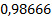
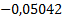
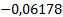
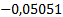
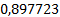
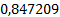
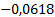
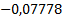
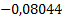
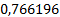
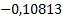
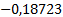
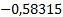
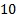
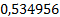
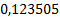
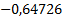
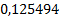
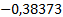
Геометрическая интерпретация данного метода выглядит следующим образом (Рис. 3):

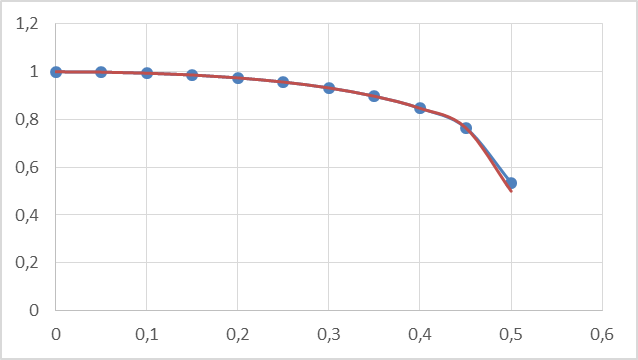
Рис. 3. Графическая интерпретация метода Рунге-Кутта

Метод Адамса

Введем вспомогательную функцию 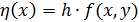. Для расчетов будем использовать метод Адамса с разностями третьего порядка, следовательно, исходя из второго интерполяционного полинома Ньютона и дополнительных преобразований имеем:

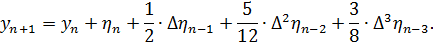
Поскольку были выбраны разности третьего порядка, то необходимо заранее вычислить 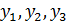. Для этого воспользуемся расчетами из метода Рунге-Кутта и подставим их в наши вычисления, которые представлены в таблице 4.

Таблица 4

 

 

 

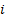
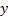
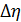
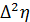
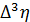
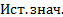
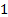
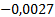
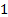
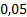
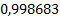
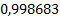
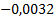
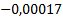
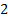
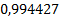
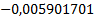
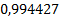
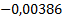
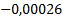
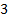
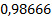
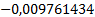
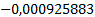
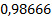
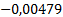
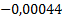
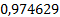
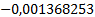
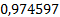
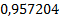
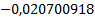
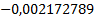
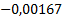
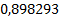
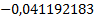
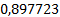
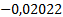
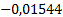
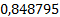
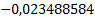
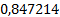
Геометрическая интерпретация данного метода выглядит следующим образом (Рис. 4):

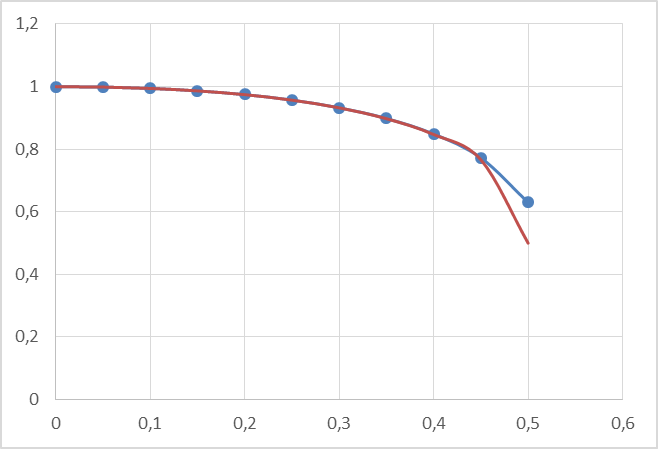
Рис. 4. Графическая интерпретация метода Адамса

Метод Милна

При использовании этого метода необходимо вычислять грубое значение 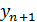, основываясь на формуле прогноза, которая выстроена за счёт первого интерполяционного полинома Ньютона, а затем необходимо воспользоваться формулой коррекции, которая получена на основе формулы Симпсона, чтобы уточнить значение .

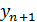Формула прогноза имеет вид:

Формула для коррекции:

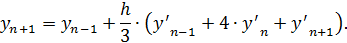
Недостающие значения 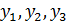возьмем из метода Рунге-Кутта.

 

Полученные вычисления представим в таблице 5.

Таблица 5

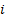
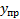
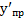
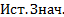
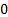
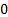
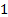
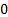
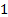
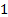
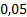
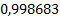
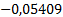
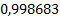
	Поделиться: Поиск по сайту ©2015-2025 poisk-ru.ru Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2019-07-29 Нарушение авторских прав и Нарушение персональных данных	 Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд Тема 11. Банковские риски и способы их оценки Опросник «Активность повседневной жизни» Интересно: Как правильно принимать препараты кальция? Как защитить исследовательскую работу (проект) Роль энергетики в жизни и развитии общества Что такое цифровой прототип? Обратная связь