Дифференциальным уравнением с разделяющимися переменными
Однородной функцией нулевого измерения является:
f(x)= 
f(x)= 
f(x)= 
Один из корней характеристического уравнения равен нулю для дифференциального уравнения (-ий):


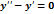
Решением дифференциального уравнения y’-у = 0 является функция:
у=0
у=ех
Матрица 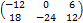 равна произведению:
равна произведению:
-2 

3 
Длина вектора 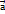 =
=  :
:
Lne
Lg10
7lne2
Даны векторы 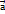 и
и 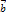 . Значения скалярного произведения векторов
. Значения скалярного произведения векторов 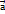 и
и 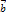 принадлежат интервалу (-3;1) для векторов:
принадлежат интервалу (-3;1) для векторов:
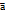 (-1;2;-3) и
(-1;2;-3) и 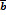 (2;2;-3)
(2;2;-3)
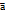 (-1;2;2) и
(-1;2;2) и 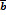 (2;-4;4)
(2;-4;4)
Прямая x+2y-4=0:
отсекает на оси Ох отрезок а=4
отсекает на оси Оу отрезок b=2
Точка Е(-2;3) является серединой отрезка, заданного точками:
А(0;1) и В(-4;5)
А(-2;2) и В(-2;4)
А(2;-1) и В(-6;7)
Точка С(-1;2) является центром окружности:
(х+1)2+(у-2)2=4
х2+2х+у2-4у-4=0
Значение предела: 
2* 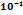
Предел  равен:
равен:
 lg1000
lg1000
3* 
Значение объем тела, полученного при вращении вокруг оси ОХ фигуры, ограниченной линиями 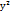 =2х,х=1 принадлежит промежутку:
=2х,х=1 принадлежит промежутку:
(3;6)
(1;4)
Интеграл  равен:
равен:
2ln 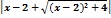 +C
+C
2ln  +C
+C
ln 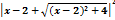 +C
+C
Площадь фигуры,ограниченной линиями у=2-  ,у=
,у=  равна:
равна:
2,(6)
2 
8* 
Площадь фигуры,ограниченной линиями у=4-  ,у=0 равна:
,у=0 равна:
 *
* 
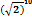 *
* 
 *
* 
Значение полного приращения функции z= 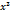 +
+  в точке Р(1;-2),если Δх=-0,01, Δу=0,02,принадлежит промежутку:
в точке Р(1;-2),если Δх=-0,01, Δу=0,02,принадлежит промежутку:
(-2;1)
(-3;0)
Приближенное значение числа  принадлежит промежутку:
принадлежит промежутку:
(1;4)
(0;3)
Значение длины дуги кривой  =
=  , отсеченной прямой х=
, отсеченной прямой х=  принадлежит промежутку:
принадлежит промежутку:
(1;3)
(2;5)
Значение площади фигуры, ограниченной линиями у=  +4х, у=х+4 принадлежит промежутку:
+4х, у=х+4 принадлежит промежутку:
(19;22)
(18;21)
Один из стационарных точек функции z=2  +х
+х 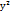 +5
+5  +
+ 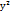 +1 имеет координаты:
+1 имеет координаты:
(0;0)
Для функции z=2  +х
+х 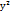 +5
+5  +
+ 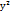 +1 верны утверждения:
+1 верны утверждения:
(-1;2)- экстремума нет
Если А=  ; В=
; В= 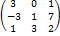 , то сумма А+В равна:
, то сумма А+В равна:
 ;
; 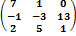
Система 
Имеет единственное нулевое решение
Однородная
Матричный метод для решения систем линейных алгебраических уравнений можно применить, если:
Система однородная и основная матрица системы невырожденная
Скалярное произведение векторов: 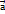 = {1,2,3},
= {1,2,3}, 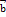 = {-1,2,-2}
= {-1,2,-2}

Точки М1 (1;5) и М2 (1;5) лежат на прямой:
4x-y+1=0;
 ;
;
 =
=  ;
;
Плоскость 2x-3y+z-6=0:
параллельна вектору 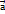 (2;1;-1)
(2;1;-1)
отсекает на оси Oy отрезок b=-2
Число R=3 является радиусом окружности:
x2-2x+y2+4y-4=0
(x+2)2+(y-1)2=5
Значение предела  принадлежит интервалу:
принадлежит интервалу:
(1;4)
(0;3)
(2;5)
Угловой коэффициент касательной к кривой f(x) =  в точке x= -1 равен:
в точке x= -1 равен:
 lg10
lg10
 lg10
lg10

Вторая производная функция f(x)=  -2x2+4x-5 в точке x = 0 равна:
-2x2+4x-5 в точке x = 0 равна:
-4×10
-4×60
-4×50
Если С= 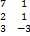 D=
D=  то разность С-D равна:
то разность С-D равна:
B) 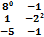
D) 
Е) 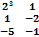
Дифференциальным уравнением второго порядка является:
C) уʹʹ=sin9x D) yʹ+xyʹʹ=7
Дифференциальным уравнением третьего порядка является:
D) уʹ+5у=уʹʹ
Порядок дифференциального уравнения уʹ×Х3=у2 равен числу из промежутка:
А 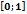
С 
Е (0;2)
Дифференциальным уравнением первого порядка является:
B (4+х)уʹ=х2-1
D) уʹ +5y= 
F) уʹ=x2+6x-8
Значение определителя 
D) 41 
G) 41lg10
Даны вектора 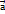 =(4; -2;-4),
=(4; -2;-4), 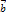 =(6;-3;2). Тогда для скалярного произведения справедливо:
=(6;-3;2). Тогда для скалярного произведения справедливо:
С) 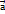 ×
×  =
=  ×
× 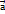
Найти алгебраическое дополнение А13 матрицы 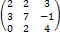 :
:
12/  ;
;

Найти алгебраическое дополнение А22 матрицы 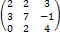 :
:
16/2;
Радиус окружности x2+y2=9 равен:
Укажите условие параллельности прямых A1x+B1y+C1=0 и A2x+B2y+C2=0:


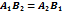
Вычислить предел: 

Область определения функции y=x2-1 равна:

(-∞;-1) U (-1;1) U(1;∞)
Х – любое значение
Порядок диффенциального уравнения  равен:
равен:
31
Тригонометрическая форма комплексного числа 1+i  :
:
2(Cos2π/6+ i sin2π/6)
2 (cos  + i sin
+ i sin  )
)
Найти интеграл 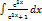 :
:
 ln
ln 


 ln
ln 
Найти интеграл 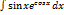 :
:
-1/ 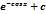
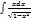 найти интеграл:
найти интеграл:
- 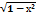 +с
+с
-  +с
+с
- 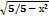 +с
+с
Дано: z =  . Найти
. Найти 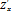
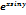 sin y
sin y
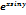 sin
sin 
Дано: z =  . Найти
. Найти 
–x3y-2
- 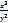
- 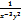
Общее решение дифференциального уравнения ху’ = 2у имеет вид:
ln 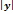 = lnCx2
= lnCx2
Решить уравнение y”=x+sinx:
y=  +cosx+
+cosx+  x+
x+ 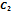
y= 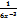 -sinx+
-sinx+  x+
x+ 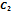
Необходимое условие сходимости выполняется для следующих рядов:

Область сходимости  степенного ряда:
степенного ряда:
[-  ]
]
Область сходимости  степенного ряда:
степенного ряда:
[-1;1]
[-0,01*  ]
]
Значение интеграла  dx c точностью до 0,001 равно:
dx c точностью до 0,001 равно:
0,245
24,5* 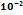
2,45* 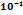
Сходящиеся числовые ряды:
1-  +
+  -…+
-…+ 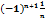 +…
+…
1+ 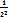 +
+  +…+
+…+  +…
+…
1- 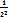 +
+  -…+
-…+  +…
+…
В ящике 8 деталей,из них 6 окрашенных.Взяли пять деталей. Найти вероятность того, что три из них окрашенны:
5/14
5/7 
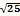 /14
/14
Случайная величина Х задана функцией распределения
Найти математическое ожидание случайной величины Х:
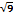
9/ 
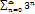 (1).
(1).  (2).
(2). 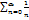 (3) какой из данных радов сходится:
(3) какой из данных радов сходится:
4\2
8\4
Абсолютно сходящиеся числовые ряды:
1- 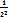 +
+  -…+
-…+  +…
+…
1- 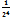 +
+ 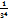 -…+
-…+  +…
+…
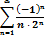
В партии из 8 деталей – 6 стандартные. На удачи отобраны 5 деталей. Найти вероятность того, что среди отобранных деталей 3 стандартные:
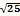 /14
/14
5/7 
Случайная величина Х задана функцией распределения:
| Х | ||||
| Р | 0,1 | 0,4 | 0,3 | 0,2 |
Найти математическое ожидание случайной величины Х:
6,4
8 
Найти минор 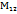 матрицы
матрицы 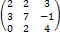
Найти алгебраическое дополнение  матрицы
матрицы 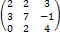
4/2
Найти угловой коэффициент прямой 7х-2у+3=0
14/4
3, 5
7/2
Вычислить интеграл 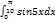 :
:
0,2
3/5
1/5
Дано: z=(x2+y2)3. Найти: Z’x:
2 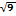 x(x2+y2)2
x(x2+y2)2
6x(x2+y2)3
Найти для функции Z=7x3y- 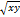 значение выражения Z’y в точке А (1;1):
значение выражения Z’y в точке А (1;1):
13/2
6,5
Решите уравнение yy’+x=0:
x2+y2=2c
Общее решение дифференциального уравнения yn-5y’+6y=0 имеет вид:
y=C1e2x+C2e3x
y= e3x (C1e-x+C2)
y= e2x (C1+C2ex)
Общее решение дифференциального уравнения y’=e2x имеет вид:
y=  e2x +C
e2x +C
2y = e2x + C
Общее решение дифференциального уравнения yn-2y’+2y=0 имеет вид:
y= ex (C1cosx+C2sinx)
y= ex cosx (C1+C2tgx)
Укажите общее уравнение плоскости в пространстве:
Ax+By+Cz+D=0
A1x+B1y+C1z+D1=0
A2x+B2y+C2z+D2=0
Вычислить предел: 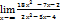

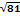
Вычислить предел: 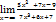
0/8
0/4
Найдите промежуток убывания функции у=х2- 
(- 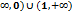
(- 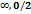 )
) 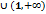
Найти производную второго порядка функции у=х 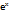 в точке х=0:
в точке х=0:
6/3
4/2
Найти производную функцию  если t=1 y’(t=1)
если t=1 y’(t=1)

Производная функции у= 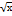 +ln(5x+1) равна:
+ln(5x+1) равна:
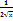 +
+ 

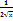 +
+ 
Математика.ВОУД.Караганда-2014
 равен:
равен:
31  +C
+C
C+31 
4y”-8y’+5y=0 найти общее решение дифференциального уравнения:
 x)
x)
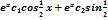 x)
x)
y”+2y’+y=0 найти общее решение дифференциального уравнения:


Вероятность достоверного события:
Р=1
Р= 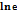
Р= 
Вероятность невозможного бытия:
Р= 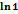
Р=0
Р=1- 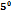
Вероятность противоположного события:
Р( 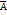 )=1-р(А)
)=1-р(А)
Р( 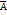 )=-р(А)+1
)=-р(А)+1
Вероятность случайного события принимает значение:
0≤р≥1
Ln1<p<lne
Ln1< 
Вычислите алгебраическое дополнение  для определителя
для определителя 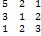
5 
Вычислите определитель 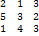 :
:
40* 
40 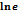
Вычислите определитель 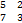 :
:

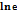
Вычислите сумму матриц ( )+(
)+( ):
):
( 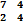 )
)
(  )
)
( 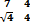 )
)
Вычислить 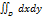 ,где D=(0≤x≤1; 0≤y≤1):
,где D=(0≤x≤1; 0≤y≤1):

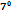
Вычислить 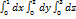 :
:
2* 
3* 
Вычислить длину вектора а=(6,3,-2):

14- 
Вычислить интеграл  :
:
C- 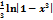
- 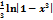 +C
+C
Вычислить интеграл  :
:


Вычислить интеграл 
 cos(a-bx)+C
cos(a-bx)+C
 cos(a-bx)+C
cos(a-bx)+C
Вычислить интеграл 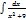 :
:
 arctg
arctg  +C
+C
 arctg
arctg  +C
+C
Вычислить интеграл  :
:
 +C
+C
0.2 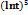 +C
+C
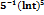 +C
+C
Вычислить интеграл  dx:
dx:
2 


Вычислить интеграл  dx:
dx:
E-1)
E-3
-3+3e
Вычислить интеграл 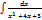 :
:
Arctg(x+2)+C
Arctg (2+x)+C
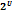 arctg(x+2)+C
arctg(x+2)+C
Вычислить интеграл 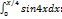
½
0.5
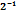
Вычислить интеграл  :
:
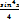 +C
+C
 x+C
x+C
0.25  x+C
x+C
Вычислить интеграл 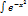 xdx:
xdx:
- 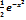 +C
+C
C- 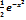
C-0.5 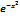
Вычислить интеграл 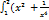 )dx:
)dx:


2 
Известно, что f(х)=5  . Найти
. Найти 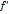 :
:
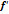 = 20
= 20 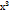
Какие векторы коллинеарные:
С=  , d=
, d= 
С=  , d=
, d= 
Какие векторы ортогональные:
С=  , d=
, d= 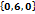
С=  , d=
, d= 
С= 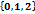 , d=
, d= 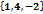
Какое из следующих чисел может являться эксцентриситетом эллипса:
0,2
0,5
1\5
Какой из следующих векторов является нормальным вектором к плоскости 3х-у+2z-5=0
А= 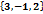
Квадратная матрица А называется вырожденной, если
detA=0
detA=ln1
detA=lne- 
Малая полуось эллипса равна 24, а расстояние между фокусами 2с=20. Определить большую полуось эллипса:
Lne
2(15-  )
)
Найти 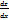 , если z=
, если z=  +2
+2 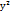 +у+1
+у+1
2х
4у+1
Найти  функции z=
функции z= 
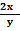
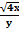
Найти  , если z=xy+2
, если z=xy+2 
X+4y
2 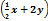
Найти  , если z= 5xy+
, если z= 5xy+  +
+ 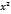 +1
+1
10- 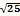
5· 
Найти cos ɑ между векторами с= 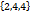 и d=
и d= 
cos ɑ=8\9
cos ɑ= 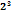 \
\ 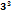
Найти у, если у=sin2x:
Coas2x
-2(-cos2x)
Найти  , если z=5xy+
, если z=5xy+  +
+ 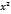 +1
+1


2· 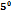
Найти 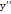 , если у(х)=ln(3х):
, если у(х)=ln(3х):
- 
- 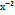
- 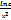
Найти действительную полуось гиперболы 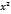 -4
-4  -36=0:
-36=0:

12- 
Вычислить интеграл  dх:
dх:
 +С
+С
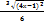 +С
+С
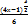 + С
+ С
Вычислить минор 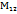 для определителя
для определителя  :
:

14- 
Вычислить несобственный интеграл  :
:
⧝
Вычислить площадь, ограниченную линиями: у= 4  , у=0:
, у=0:
32\3
10 
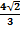
Вычислить предел  :
:
1\3

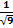
Вычислить предел  :
:
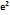

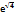
Вычислить предел 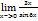 :
:
1\2
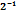
0,5
Вычислить расстояние от точки М(12,12) до прямой 3х+4у-2=0:
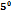
Lne
Вычислить угловой коэффициент прямой, проходящий через две данные точки М1(2,-5) и М2(3,2):
7,  , 14-
, 14- 
Геометрический смысл  :
:
Площадь криволинейной трапеции
Говорят, что ряд  сходится, если:
сходится, если:
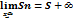
Для функции f(x)= 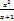 определить критические точки:
определить критические точки:
-2 и 0
- 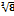 и 0
и 0
-2lne и 0
Если в определитель поменять местами две строки, то определитель:
Изменит знак
Если уравнение поверхности задано в форме z=f(x,y), то уравнение касательной плоскости в точке М( ,
,  ) имеет вид:
) имеет вид:
z-  =
= 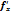 (
( 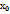 ,
, 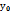 )(X-
)(X- 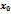 )+
)+ 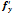 (
( 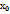 ,
, 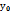 )(Y-
)(Y-  )
)
Формула дисперсии случайной величины Х:
D(X)=M(  )-
)- 
D(X)=  +
+ 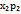 +…+
+…+ 
Формула интегрирования по частям:
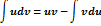
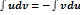 +uv
+uv
Формула математического ожидания непрерывной величины Х:
M(Х)= 
Формула первого замечательного предела:
 =1
=1
 =1
=1
Формула сложения вероятностей нечетной для всех х из области определения, если:
Р(А+В)=Р(А)+(В)
Функция f(x) называется нечетной для всех х из области определения, если:
F(-x)=-f(x)
-f(x)=f(-x)
Функция f(x) называется первообразной для функции f(x), если для всех х выполняется равенство:
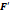 (х)=f(х)
(х)=f(х)
Функция f(x) называется четной для всех х из области определения, если:
F(-x)=f(x)
f(x)=f(-x)
Чему равен  :
:
F(b)-F(a), где 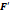 (х)=f(х)
(х)=f(х)
-F(b)+F(a), где 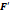 (х)=f(х)
(х)=f(х)
Что означает обозначение  :
:
Определенный интеграл
Найти площадь фигуры, ограниченной линиями 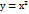 -2, у=х; 9/2,(2/9)-1,4,5
-2, у=х; 9/2,(2/9)-1,4,5
Найти предел  А)
А) 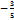 С)-0,6 Е)
С)-0,6 Е)  -1
-1
Найти предел  А) 1 Е)lne G) 20
А) 1 Е)lne G) 20
Найти предел 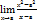 В) 2а D)
В) 2а D) 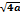 F)
F) 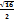 a
a
Найти производную функции у=х3sin3x A) y’=3x2(sin3x+xcosx) C) y’=3x2sin3x +3x3cos3x
Найти производную функции 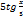 : В)
: В) 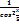 D)cos-2
D)cos-2  H) (cos
H) (cos  )-2
)-2
Найти производную функции y=3x3+53  B) y’=9x2+
B) y’=9x2+  +
+ 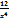 C) y’=9x3-
C) y’=9x3- 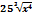 -
- 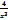 D) y’=
D) y’=  +
+ 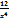 +9x2
+9x2
Найти промежутки возрастания функции у=  А)(-
А)(-  D) 3
D) 3 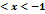
Найти расстояние между точками А(2,-3) и В(-1,-7) 5; 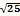 ; 10-
; 10- 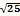
Найти скалярное произведение векторов с={1,1,2} и d={2,1,0} B)=3 D)=3lne E) 
Найти уравнение вертикальной асимптомы для функции у= 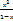 А) х=1 С) х-1=0 D) 1-х=0
А) х=1 С) х-1=0 D) 1-х=0
Найти числа А и B при которых 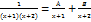 А) А=1 B=-1 D) A=2u B=-1
А) А=1 B=-1 D) A=2u B=-1
Неверное свойство математического ожидания: F) M(X+Y)2= M2(X)+M2(Y) G) M(X+Y)2= M2(X)+2M(XY)+M2(Y) H) M(X+Y)2= M2(X)-2M(XY)+M2(Y)
Объем тела вращения вокруг оси ОХ: А) Vx=π  2(x)dx C) Vx=
2(x)dx C) Vx= 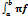 2(x)dx
2(x)dx
Объем тела с областью Т вычисляется по следующей формуле В) 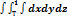
Определитель с двумя пропорциональными строками: равен нулю
Определить точки максимума у= 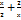 В) -2lne E) -
В) -2lne E) -  F) -
F) - 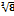
По какой формуле вычисляется площадь фигуры, ограниченной линиями: y=f(x), y=φ(x) на [a,b], где f(x)˃ φ(x) D) 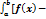 φ(x)]dx F)
φ(x)]dx F) 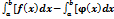
Предел отношения приращения функции 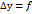 (x0+
(x0+ 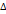 x)-f(x0) к приращению аргумента
x)-f(x0) к приращению аргумента 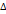 x при стремлении
x при стремлении 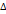 x к нулю называется: В) производной функции f(x)
x к нулю называется: В) производной функции f(x)
При каком р прямая рх+3у-7=0 параллельна прямой 2х+3у+4=0 В) 2 Е) 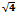 Н) lo
Н) lo