Определенный интеграл, его свойства. Геометрический смысл определенного интеграла. Интегрирование заменой переменной в определенном интеграле
Понятие определенного интеграла
Пусть функция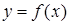 
определена на отрезке 
, 
. Разобьем этот отрезок на n произвольных частей точками:
.
Обозначим это разбиение Т, а точки 
назовем точками разбиения. В каждом отрезке 
выберем произвольную точку 
. Через 
обозначим разность 
, которая является длиной отрезка .
Образуем сумму:
, (1)
которую назовем интегральной суммой для функции 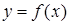на отрезке , соответствующей данному разбиению Т.
Для данной функции 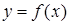на отрезке можно составить бесчисленное множество интегральных сумм, так как построение интегральной суммы состоит в произвольном делении заданного отрезка на элементарные отрезки и произвольном выборе точки на каждом элементарном отрезке.
 |
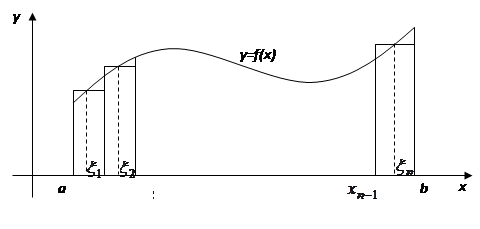Рис. 1
Из рисунка 1 следует геометрический смысл суммы 
: это сумма площадей прямоугольников с основаниями 
и высотами 
, если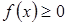 
.
Обозначим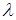 
длину наибольшего отрезка разбиения: 
.
Определение: Если существует конечный предел I интегральной суммы (1) при 
, то этот предел называется определенным интегралом от функции 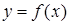на отрезке и обозначается:
, (2)
или 
.
В этом случае функция 
называется интегрируемой на отрезке . Для интегрируемости достаточно, чтобы функция была непрерывна на отрезке или имела конечное число разрывов первого рода. Числа a и b называются соответственно нижним и верхнимпределами интегрирования, - подынтегральной функцией, x – переменнойинтегрирования.
Основные свойства определенного интеграла
Определенный интеграл обладает следующими свойствами.
1. При перестановке пределов интегрирования определенный интеграл меняет свой знак на противоположный: 
. Если пределы интегрирования равны между собой, то 
.
2. Каковы бы ни были числа a, b, c, имеет место равенство:
. Это равенство верно, если 
и верно при любом с, если существуют любые два из фигурирующих в нем трех интегралов.
3. Постоянный множитель можно выносить за знак определенного интеграла, т.е.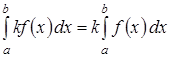 
, где k – постоянная величина.
4. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е. 
.
Замечание. Свойство 4 справедливо для любого конечного числа слагаемых.[2]
Вычисление определенного интеграла
Формула Ньютона – Лейбница
Вычисление определенных интегралов методом, основанным на определении интеграла как предела интегральной суммы, связано с большими трудностями. Для удобства вычисления определенных интегралов применяется формула Ньютона – Лейбница:
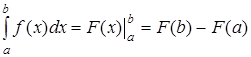, (3)
где 
- первообразная для подынтегральной функции 
. Она находится при вычислении соответствующего неопределенного интеграла: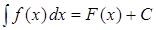 
.
Формула Ньютона – Лейбница принадлежит к числу важнейших формул высшей математики. С ее помощью можно просто и точно вычислять значения определенных интегралов, а с их помощью находить значения различных величин, например, площади криволинейных фигур, длины дуг кривых и т. д.
Пример 1.
.
Пример 2.
.
Пример 3.
.
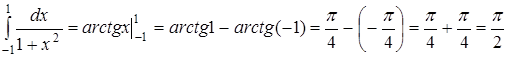