Если плоская фигура, ограниченная осью Ох, прямыми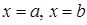 
и графиком непрерывной функции 
, вращается вокруг оси Ох, то объем полученного тела вычисляется по формуле
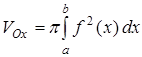. (8)
Если плоская фигура, ограниченная осью Оу, прямыми 
и графиком непрерывной функции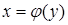 
, вращается вокруг оси Оу, то объем полученного тела находим по формуле
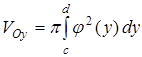. (9)
Пример 9.
Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной гиперболой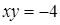 
, осью абсцисс и прямыми 
.
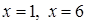Решение.
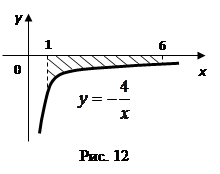Построим указанные линии. По формуле (8) будем иметь:
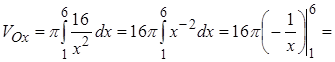
(куб.ед.).
Пример 10.
Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, заключенной между линиями, заданными уравнениями 
.
Решение. Искомый объем определяется разностью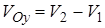 
, где 
- объем тела, образованного вращением вокруг оси Оу треугольника ОАВ;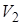 
- объем тела, образованного вращением вокруг оси Оу криволинейной трапеции ОСАВ.
Чтобы найти пределы интегрирования, определим координаты точек пересечения линий:
откуда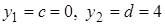 
.
По формуле (9) получим:
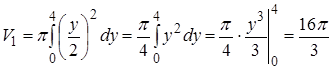(куб.ед.)
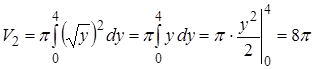(куб.ед.)
Тогда 
(куб.ед) [8]
Упражнения для закрепления
1. Вычислить определенный интеграл:
а) 
;
б) 
в)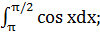 
г) 
д) 
е)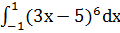 
;
ж)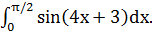 
2. Вычислить площадь, ограниченную заданными линиями. Выполнить чертеж.
а) 
б) 
в) 
г)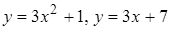 
д)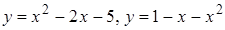 
е)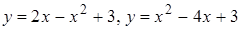 
ж)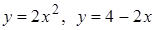 
з) 
2. Вычислить объем тела, образованного вращением вокруг координатных осей фигуры, ограниченной указанными линиями. Выполнить чертеж.
а)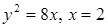 
вокруг оси Ох
б)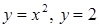 
вокруг оси Оу
в) 
вокруг оси Оу;
г) 
вокруг оси Ох;
д)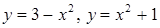 
вокруг оси Оу.
Контрольные вопросы
1. Какая фигура называется криволинейной трапецией?
2. Напишите формулу для вычисления площади криволинейной трапеции.
3. Напишите формулы для вычисления объемов тела вращения.
4. Что называется интегральной суммой функции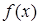 
на отрезке 
?
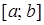5. Что называется определенным интегралом?
6. Перечислите основные свойства определенного интеграла.
7. Напишите формулу Ньютона – Лейбница.
8. В чем состоит способ подстановки в определенном интеграле? Найдя новые пределы интегрирования, следует ли переходить к первоначальной переменной интегрирования и данным пределам интегрирования?
Решение прикладных задач с помощью определенного интеграла
Путь, пройденный точкой
Если точка движется прямолинейно и ее скорость v=f(t) есть известная функция времени t, то путь, пройденный точкой за промежуток времени t1≤t≤t2, вычисляется по формуле S= 
. (1)
Пример 1. Две точки движутся по одной и той же прямой: одна со скоростью v1=3t2+2t, другая – со скоростью v2=8t+10 (v1 и v2 – в м/с, t –в секундах). Предполагая, что в начале движения они были вместе, найти, когда и на каком расстоянии от начала движения они снова окажутся вместе.
Решение. Используя формулу (1), найдем путь, пройденный каждой точкой от начала движения до момента t:
S1=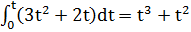 
; S2=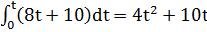 
Так как по условию S1=S2, то 
, откуда t1=0, t2= - 2, t3=5. Значит, движущиеся точки окажутся вместе через 5с. При этом каждая из них пройдет путь S1=S2=4∙52+10∙5=150(м).
Работа переменной силы
Если переменная сила F=F(x) действует на направлении оси Ох, то работа силы на отрезке а≤х≤b вычисляется по формуле
А= 
(2)
Пример 2. Найти работу, которую нужно совершить при растяжении пружины на 0,02м, если для ее растяжения на 1см требуется сила 10Н.
Решение. Согласно закону Гука, сила F, растягивающая или сжимающая пружину на х метров, равна kx, где k – коэффициент пропорциональности. Из условия следует, что 10=k∙0,01, т.е. k=1000, и, значит, F=kx=1000x. Теперь по формуле (2) найдем искомую работу:
А=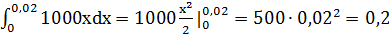 
(Дж).
Сила давления жидкости.
Пусть пластинка в виде криволинейной трапеции погружена вертикально в жидкость с плотностью ρ так, что ее боковые стороны параллельны поверхности жидкости и находятся ниже уровня на расстояниях а и b. Для нахождения силы давления жидкости на пластинку разобьем ее на n малых горизонтальных полосок прямыми, параллельными оси Оу и проходящими через точки х0=а, х1, …, хn-1, хn=b. Выделим одну из полосок, находящуюся на глубине хi. Для такой достаточно узкой полоски давление во всех ее частях можно приближенно считать одинаковым, а саму полоску принять за прямоугольник с высотой ∆ хi=(b-a)/n. Длина основания этого прямоугольника есть некоторая функция от х, которую обозначим f(x). Согласно закону Паскаля, сила давления Рi на i-ю полоску составляет
Pi=ρgf(хi) хi∆ хi,
а сила давления жидкости на всю пластинку вычисляется по формуле
P=ρg 
, (3)
Рис.1
Пример 3.Пластинка, имеющая форму треугольника с основанием 4см и высотой 3см, погружена вертикально в воду. Вычислить силу давления на эту пластинку, если ее вершина лежит на поверхности воды, а основание параллельно ей (рис.2)
Решение. Здесь а=0, b=ВЕ=0,03м, АС=0,04м, ρ=1000кг/м3. Пусть DF-ширина пластинка на уровне ВК=х. из подобия ∆АВС и ∆DBF находим
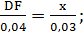DF=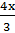 
,
Подставляя все данные в формулу (3), получим
Р=1000∙9,81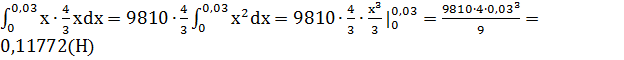 
Рис.2