Тема: Позиционные системы счисления.
Что проверяется:
Знание позиционных систем счисления.
1.4.1. Позиционные системы счисления.
1.1.3. Умение строить информационные модели объектов, систем и процессов в виде алгоритмов(?).
Что нужно знать:
· принципы кодирования чисел в позиционных системах счисления
· 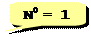 чтобы перевести число, скажем, 12345N, из системы счисления с основанием
чтобы перевести число, скажем, 12345N, из системы счисления с основанием  в десятичную систему, нужно умножить значение каждой цифры на
в десятичную систему, нужно умножить значение каждой цифры на  в степени, равной ее разряду:
в степени, равной ее разряду:
4 3 2 1 0 ← разряды
1 2 3 4 5N = 1·N4 + 2·N3 + 3·N2 + 4·N1 + 5·N0
· последняя цифра записи числа в системе счисления с основанием  – это остаток от деления этого числа на
– это остаток от деления этого числа на 
· две последние цифры – это остаток от деления на 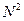 , и т.д.
, и т.д.
· число 10N записывается как единица и N нулей: 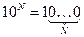
· число 10N-1 записывается как N девяток: 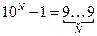
· число 10N-10M = 10M · (10N-M – 1) записывается как N-M девяток, за которыми стоят M нулей: 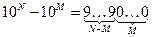
· число 2N в двоичной системе записывается как единица и N нулей: 
· число 2N-1 в двоичной системе записывается как N единиц: 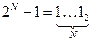
· число 2 N– 2 K при K < N в двоичной системе записывается как N–K единиц и K нулей: 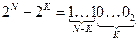
· поскольку 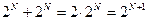 , получаем
, получаем 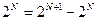 , откуда следует, что
, откуда следует, что 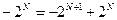
· число 3N записывается в троичной системе как единица и N нулей: 
· число 3N-1 записывается в троичной системе как N двоек: 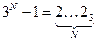
· число 3N – 3M = 3M · (3N-M – 1) записывается в троичной системе как N-M двоек, за которыми стоят M нулей: 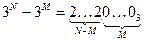
· можно сделать аналогичные выводы для любой системы счисления с основанием a:
- число aN в системе счисления с основанием a записывается как единица и N нулей: 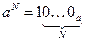
- число aN-1 в системе счисления с основанием a записывается как N старших цифр этой системы счисления, то есть, цифр (a-1): 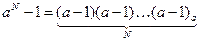
- число aN – aM = aM · (aN-M – 1) записывается в системе счисления с основанием a как N-M старших цифр этой системы счисления, за которыми стоят M нулей: 
Пример задания:
Р-25. (демо-2021) Значение арифметического выражения: 497 + 721 – 7 – записали в системе
счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
Решение:
1) приведём все числа к степеням семерки, учитывая, что 49 = 72
714 + 721 – 71
2) расставим степени в порядке убывания:
721 + 714 – 71
3) Очевидно, что «шестёрки» в семеричной записи значения выражения возникнут только за счёт вычисления разности 714 – 71, их количество равно 14-1=13
4) Ответ: 13.
Решение (использование программы):
1) язык Python позволяет работать с большими числами, не задумываясь о том, что для их хранения требуется больше памяти, чем для «обычного» целого числа (когда значение не помещается в 4 байта, интерпретатор автоматически переходит на представление числа в виде массива с «длинной арифметикой»)
2) поэтому может быть написана программа, которая вычисляет нужное значение и методом деления в столбик определяет все цифры его записи в семеричной системе счисления; шестёрки считаем с помощью счётчика count6:
x = 49**7 + 7**21 - 7
count6 = 0
while x:
if x % 7 == 6: count6 += 1
x //= 7
print(count6)
3) Ответ: 13.
Решение (использование программы в среде Pascal ABC.NET, А. Агафонцев):
1) Pascal ABC.NET за счет использования фреймворка.NET позволяет воспользоваться типом System.Numerics.BigInteger (предназначенным для произвольно больших целых со знаком) и связанными с ним функциями.
2) Таким образом, программа получается во многом схожей с программами на Python. Особо отметим, что использование функций возведения в степень не связанных с типом BigInteger для систем с основанием, не являющимся степенью двойки, приводит к неверным результатам из-за использования вещественных чисел. Например, BigInteger(power(9,34)) или BigInteger(9 ** 34) преобразуют вещественное число в целое произвольно большой длины, но еще при операции возведения в степень потеряется часть идеальной, математической мантиссы.
3) В связи с вышесказанным допустимо только использование записей вида BigInteger.Pow(9,34).
4) Полная программа:
Var
a: BigInteger;
k: int64;
Begin
a:= BigInteger.Pow(49, 7) + BigInteger.Pow(7, 21) - 7;
k:= 0;
while (a > 0) do
Begin
if (a mod 7 = 6) then
k:= k + 1;
a:= a div 7;
end;
writeln(k);
End.
5) Ещё одно решение на PascalABC.NET (П.Е. Финкель)
Begin
var k:=0;
var x:=49bi**7+7bi**21-7;
while x>0 do begin
if x mod 7=6 then k+=1;
x:=x div 7;
end;
println(k);
End.
6) здесь «bi» длинным, а ** означает возведение в степень
7) Ответ: 13.
Решение (использование программы на Java, М. Коротков):
1) язык Java позволяет работать с большими числами с помощью типа BigInteger;
2) может быть написана программа, которая вычисляет значение арифметического выражения и методом деления в столбик определяет все цифры его записи в семеричной системе счисления; шестёрки считаем с помощью счётчика amt6:
3) полная программа:
import java.math.BigInteger;
public class Main {
public static void main(String[] args) {
final BigInteger SIX = BigInteger.valueOf(6);
final BigInteger SEVEN = BigInteger.valueOf(7);
final BigInteger NUM1 = BigInteger.valueOf(49).pow(7);
final BigInteger NUM2 = BigInteger.valueOf(7).pow(21);
BigInteger num = NUM1.add(NUM2).subtract(SEVEN);
BigInteger amt6 = BigInteger.ZERO;
while (!num.equals(BigInteger.ZERO)) {
if (num.mod(SEVEN).equals(SIX)) {
amt6 = amt6.add(BigInteger.ONE);
}
num = num.divide(SEVEN);
}
System.out.println(amt6);
}
}
4) Ответ: 13.
Ещё пример задания:
Р-24. (М.В. Кузнецова) Значение арифметического выражения: 6410 + 290 - 16 записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?
Решение:
1) Приведём все числа к степеням восьмерки, учитывая, что 16 = 64 - 48 =82-6∙81
6410 + 290 - 16 = (82)10 + 23∙30 – (82 – 48) = 820 + 830 – 82 + 6∙81
2) Перепишем выражение, располагая степени восьмёрки в порядке убывания:
820 + 830 – 82 + 6∙81 = 830 + 820 – 82 + 6∙81
3) Очевидно, что «семёрки» в восьмеричной записи значения выражения возникнут только за счёт вычисления разности 820 – 82, их количество равно 20-2=18
4) Ответ: 18.
Решение (использование программы в среде Pascal ABC.NET, А. Агафонцев):
1) В среде Pascal ABC.NET при использовании типа BigInteger задача может быть решена с помощью программы:
Var
a: BigInteger;
k: int64;
Begin
a:= BigInteger.Pow(64, 10) + BigInteger.Pow(2, 90) - 16;
k:= 0;
while (a > 0) do
Begin
if (a mod 8 = 7) then
k:= k + 1;
a:= a div 8;
end;
writeln(k);
End.
2) Ответ: 18.
3) Ещё одно решение на PascalABC.NET (П.Е. Финкель)
Begin
var k:=0;
var x:=64bi**10+2bi**90-16;
while x>0 do begin
if x mod 8=7 then k+=1;
x:=x div 8;
end;
println(k);
End.
Решение (программа на Python, Б.С. Михлин):
1) если доступна среда программирования на Python, можно написать программу, которая использует встроенную арифметику длинных чисел:
x = 64**10 + 2**90 - 16
print(oct(x).count('7'))
2) ответ: 18.
Ещё пример задания:
Р-23. (М.В. Кузнецова) Значение арифметического выражения: 99 – 39 + 919 – 19 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Решение:
1) Приведём все числа к степеням тройки, учитывая, что 19=27-8=33-(2∙31+2∙30):
99 – 39 + 919 – 19= (32)9 – 39 + (32)19 – (33 – (2∙31 + 2∙30)) = 318 – 39 + 338 – 33 + 2∙31 + 2∙30
2) Перепишем выражение, располагая степени тройки в порядке убывания:
318 – 39 + 338 – 33 + 2∙31 + 2∙30 = 338 + 318 – 39 – 33 + 2∙31 + 2∙30
3) Сначала рассмотрим часть выражения, в которой имеется два расположенных подряд «минуса»: 318 - 39 ‑ 33:
a. найдём разность двух крайних чисел: 318 – 33, в её троичной записи 18 – 3=15 «двоек» и 3 «нуля»;
b. вычтем из этого числа значение 39: одна из «двоек» (на 10-й справа позиции) уменьшится на 1, остальные цифры не изменятся;
c. итак, троичная запись разности 318 – 39 – 33 содержит 15 – 1=14 «двоек», одну «единицу» и 3 «нуля»
4) Прибавим к полученному значению сумму: 2∙31 + 2∙30 = 223. В троичной записи результата два крайних справа нуля заменяются на «двойки», остаётся один ноль. Общее количество «двоек»: 14+2=16.
5) Прибавление значения 338 не изменит количества «двоек» в троичном числе: слева от имеющихся цифр появятся ещё 38 – 18=20 «нулей» и одна «единица» – на 39-й справа позиции.
6) Итак, результат, записанный в троичной системе, содержит 39 цифр. Его состав: 16 «двоек», 2 «единицы» (их позиции: 39-я и 10-я справа) и 21 «нуль» (39-16-2=21).
7) Ответ: 16.
Ещё пример задания:
Р-22. Значение арифметического выражения: 98 + 35 – 9
записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Решение:
1) приведём все слагаемые к виду 3N и расставим в порядке убывания степеней:
98 + 35 – 9 = 316 + 35 – 32
2) первое слагаемое, 316, даёт в троичной записи одну единицу – она нас не интересует
3) пара 35 – 32 даёт 5 – 2 = 3 двойки
4) Ответ: 3.
Решение (программа, Б.С. Михлин):
1) задача может быть решена с помощью программы на Python, где есть встроенная поддержка длинных чисел:
x = 9**8+3**5-9
x3 = ''
while x:
x3 = str(x%3) + x3
x //= 3
print('Ответ:', x3.count('2'))
2) вариант без использования символьных строк:
x = 9**8+3**5-9
count2 = 0
while x:
if x % 3 == 2:
count2 += 1
x //= 3
print('Ответ:', count2)
3) Ответ: 3.
Решение (электронные таблицы, Б.С. Михлин):
1) эта конкретная задача может быть решена с помощью электронных таблиц
2) Замечание. Электронные таблицы имеют ограничения при работе с длинными целыми числами. Например, Excel при вводе больших чисел заменяет все цифры после 15-го разряда на нули. Это легко проверить, введя в ячейку число с более чем 15-ю разрядами.
Обычно электронные таблицы при этом переходят к экспоненциальному (научному) формату. Если число больше, чем 1015, то оно хранится как вещественное число (неточно). Это ограничивает использование электронных таблиц. В этой задаче заданное число меньше, чем 1015, поэтому использовать электронные таблицы можно.
3) введём заданное число, заданное арифметическим выражением, в ячейку электронной таблицы:

4) выполним алгоритм перевода числа в троичную систему: найдём в B1 остаток от деления числа на 3, а в A2 – частное:
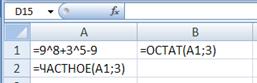
5) скопируем формулы из А2 и В1 вниз до того момента, когда частное станет равно 0 (это означает окончание процесса перевода):
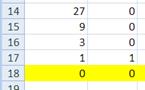
6) подсчитаем в столбце В число остатков, равных 2:
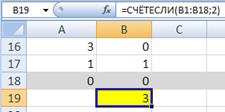
7) Ответ: 3.
8) в OpenOffice Calc нужно использовать такие формулы:
в A2: =QUOTIENT(A1;3)
в B1: =MOD(A1;3)
в B19: =COUNTIF(B1:B18;2)
Ещё пример задания:
Р-21. Сколько значащих нулей в двоичной записи числа
4512 + 8512 – 2128 – 250
Решение (способ Е.А. Смирнова, Нижегородская область):
1) Общая идея: количество значащих нулей равно количеству всех знаков в двоичной записи числа (его длине!) минус количество единиц
2) приведём все числа к степеням двойки, учитывая, что 250 = 256 – 4 – 2 = 28 – 22 – 21:
4512 + 8512 – 2128 – 250 = (22)512 + (23)512 – 2128 – 28 + 22 + 21 =
= 21536 + 21024 – 2128 – 28 + 22 + 21
3) старшая степень двойки – 21536, двоичная запись этого числа представляет собой единицу и 1536 нулей, то есть, состоит из 1537 знаков; таким образом, остаётся найти количество единиц
4) вспомним, число 2 N– 2 K при K < N записывается как N–K единиц и K нулей: 
5) для того чтобы использовать это свойство, нам нужно представить заданное выражение в виде пар вида 2 N– 2 K, причём в этой цепочке степени двойки нужно выстроить по убыванию
6) в нашем случае вы выражении
21536 + 21024 – 2128 – 28 + 22 + 21
стоит два знака «минус» подряд, это не позволяет сразу использовать формулу
7) используем теперь равенство 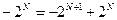 , так что – 2128 = – 2129 + 2128; получаем
, так что – 2128 = – 2129 + 2128; получаем
21536 + 21024 – 2129 + 2128 – 28 + 22 + 21
здесь две пары 2 N– 2 K, а остальные слагаемые дают по одной единице
8) общее число единиц равно 1 + (1024 – 129) + (128 – 8) + 1 + 1 = 1018
9) таким образом, количество значащих нулей равно 1537 – 1018 = 519
10) ответ: 519.
Решение (программа на Python, Б.С. Михлин):
3) если доступна среда программирования на Python, можно написать программу, которая использует встроенную арифметику длинных чисел:
x = 4**512 + 8**512 - 2**128 - 250
print(bin(x)[2:].count('0'))
4) ответ: 519.
Ещё пример задания:
Р-20. Сколько единиц в двоичной записи числа
42015 + 8405 – 2150 – 122
Решение (способ Е.А. Смирнова, Нижегородская область):
1) приведём все числа к степеням двойки, учитывая, что 122 = 128 – 4 – 2 = 27 – 22 – 21:
42015 + 8405 – 2150 – 122 = (22)2015 + (23)405 – 2150 – 27 + 22 + 21 =
= 24030 + 21215 – 2150 – 27 + 22 + 21
2) вспомним, число 2 N– 2 K при K < N записывается как N–K единиц и K нулей: 
3) для того чтобы использовать это свойство, нам нужно представить заданное выражение в виде пар вида 2 N– 2 K, причём в этой цепочке степени двойки нужно выстроить по убыванию
4) в нашем случае вы выражении
24030 + 21215 – 2150 – 27 + 22 + 21
стоит два знака «минус» подряд, это не позволяет сразу использовать формулу
5) используем теперь равенство 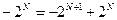 , так что – 2150 = – 2151 + 2150; получаем
, так что – 2150 = – 2151 + 2150; получаем
24030 + 21215 – 2151 + 2150 – 27 + 22 + 21
здесь две пары 2 N– 2 K, а остальные слагаемые дают по одной единице
6) общее число единиц равно 1 + (1215 – 151) + (150 – 7) + 1 + 1 = 1210
7) ответ: 1210.
Решение (С.О. Куров, Москва):
1) приведём все числа к степеням двойки, учитывая, что 122 = 128 – 4 – 2 = 27 – 22 – 21:
42015 + 8405 – 2150 – 122 = (22)2015 + (23)405 – 2150 – 27 + 22 + 21 =
= 24030 + 21215 – 2150 – 27 + 22 + 21
2) ищем в разности крайнюю левую степень двойки и крайнюю правую 21215 – 27, при этом 2150 на время «теряем»
3) определяем количество единиц в разности 21215 – 27, получаем 1215 – 7 = 1208 единиц
4) так как «внутри» этой разности есть еще 2150, то просто вычитаем одну единицу: 1208 – 1 = 1207; итого в разности 21215 – 2150 – 27 ровно 1207 единиц
5) осталось прибавить по одной единицы от чисел 24030, 22, 21
6) Ответ: 1210
Решение (программа на Python, Б.С. Михлин):
1) используется встроенная «длинная арифметика» в Python:
x = bin(4**2015 + 8**405 - 2**150 - 122)
print(x.count('1'))
2) ответ: 1210.
Ещё пример задания:
Р-19. Решите уравнение  .
.
Ответ запишите в троичной системе счисления. Основание системы счисления указывать не нужно.
Решение:
1) переведём все числа в десятичную систему счисления:

2) собирая всё в одно уравнение получаем
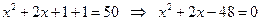
3) это уравнение имеет два решения, 6 и -8; основание системы счисления – натуральное число, поэтому ответ – 6
4) переводим ответ в троичную систему: 6 = 2∙31 = 203.
5) ответ: 20.
Решение (программа на Python, А.Н. Носкин):
1) можно (но сложнее) решить задачу перебором с помощью программы:
a = 1*7**2 + 0 + 1 # перевод "101" в 10-ю систему
c = a - 1 # число "121" в 10-й системе
for i in range(3,100):# перебираем возможные основания
b = 1*i**2 + 2*i + 1 # перевод в 10-ю систему числа "121"
if b == c:
x = i # основание системы счисления (в 10й системе)
break
x3 = ''
while x > 0:# перевод основания в 3-ю систему
x3 += str(x%3)
x //= 3
x3 = x3[::-1]# разворот числа
print(x3)
2) ответ: 20.
Решение (программа на Python, Б.С. Михлин):
3) вариант программы:
for x in range(3, 37): # среди оснований от 3 до 36
if int('121', x) + 1 == int('101', 7):
break
print('в 10 c.c:', x)
s = ''
while x:
s = str(x%3) + s
x //= 3
print('Ответ в 3 с.с:', s)
4) ответ: 20.
Ещё пример задания:
Р-18. Сколько единиц в двоичной записи числа
42014 + 22015 – 8
Решение:
1) приведём все числа к степеням двойки:
42014 + 22015 – 8 = (22)2014 + 22015 – 23 = 24028 + 22015 – 23
2) вспомним, что число 2N-1 в двоичной системе записывается как N единиц: 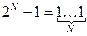 ,
,
а число 2 N– 2 K при K < N записывается как N–K единиц и K нулей: 
3) согласно п. 2, число 22015 – 23 запишется как 2012 единиц и 3 нуля
4) прибавление 24028 даст ещё одну единицу, всего получается 2012 + 1 = 2013 единиц
5) ответ: 2013.
Решение (программа на Python, Б.С. Михлин):
5) программа использует встроенную «длинную арифметику» Python:
x = bin(4**2014 + 2**2015 - 8)
print(x.count('1'))
6) ответ: 2013.
Ещё пример задания:
Р-17. Сколько единиц в двоичной записи числа
42016 + 22018 – 8600 + 6
Решение:
1) приведём все числа к степеням двойки, разложив 6 как 22+21
42016 + 22018 – 8600 + 6 = (22)2016 + 22018 - (23)600 + 22 + 21 = 24032 + 22018 – 21800 + 22 + 21
2) вспомним, что число 2N-1 в двоичной системе записывается как N единиц: 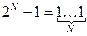 ,
,
а число 2 N– 2 K при K < N записывается как N–K единиц и K нулей: 
3) согласно п. 2, число 22018 – 21800 запишется как 218 единиц и 1800 нулей
4) прибавление 24032 даст ещё одну единицу, а прибавление 22 + 21 – ещё две, всего получается 218 + 3 = 221 единица
5) ответ: 221.
Ещё пример задания:
Р-16. Сколько единиц в двоичной записи числа
42016 – 22018 + 8800 – 80
Решение:
1) приведём все числа к степеням двойки, разложив 80 как 26+24
42016 – 22018 + 8800 – 80 = (22)2016 – 22018 + (23)800 – 22 – 21 = 24032 – 22018 + 22400 – 26 – 24
2) перестроим слагаемые в порядке уменьшения степеней двойки
24032 + 22400 – 22018 – 26 – 24
3) вспомним, что число 2N-1 в двоичной системе записывается как N единиц: 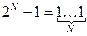 ,
,
а число 2 N– 2 K при K < N записывается как N–K единиц и K нулей: 
4) согласно п. 2, число 22400 – 22018 запишется как 382 единицы и 2018 нулей
5) добавляем старшее слагаемое 24032, получаем число 24032 + 22400 – 22018, в котором 383 единицы и в конце (после последней единицы) – 2018 нулей:

6) выделим из этого значения последнюю единицу со следующими 2018 нулями как отдельное слагаемое (число 22018):
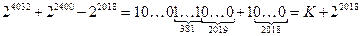 ,
,
где число K содержит 382 единицы в старших разрядах; таки образом, интересующее нас число равно 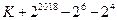
7) согласно п. 2, число 22018 – 26 запишется как 2012 единиц и 6 нулей; также выделим последнюю единицу с последующими нулями как отдельное слагаемое:
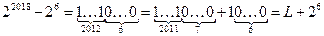
где число L содержит 2011 единиц
8) теперь остаётся найти, сколько единиц будет в двоичной записи числа 26 – 24, согласно п. 2 находим, что оно содержит 2 единицы
9) таким образом, общее число единиц равно 382 + 2011 + 2 = 2395
10) ответ: 2395.
Решение (способ 2, Е.А. Смирнов, Нижегородская область):
1) приведём все числа к степеням двойки, разложив 80 как 26+24
42016 – 22018 + 8800 – 80 = (22)2016 – 22018 + (23)800 – 22 – 21 = 24032 – 22018 + 22400 – 26 – 24
2) перестроим слагаемые в порядке уменьшения степеней двойки
24032 + 22400 – 22018 – 26 – 24
3) представим – 22018 = – 22019 + 22018 и – 26 = – 27 + 26
24032 + 22400 – 22019 + 22018 – 27 + 26– 24
4) слагаемое 24032 в двоичной записи содержит 1 единицу
5) слагаемое 22400 – 22019 содержит 381 единицу (число 2 N– 2 K при K < N в двоичной системе записывается как N–K единиц и K нулей:  )
)
6) слагаемое 22018 – 27 содержит 2011 единиц, слагаемое 26– 24 содержит 2 единицы
7) позиции единиц во всех этих слагаемых не совпадают, поэтому общее количество единиц равно 1 + 381 + 2011 + 2 = 2395
ответ: 2395
Решение (способ 3, А.И. Козлов, г. Северобайкальск):
1) приведём все числа к степеням двойки, разложив 80 как 26+24
42016 – 22018 + 8800 – 80 = (22)2016 – 22018 + (23)800 – 22 – 21 = 24032 – 22018 + 22400 – 26 – 24
2) перестроим слагаемые в порядке уменьшения степеней двойки
24032 + 22400 – 22018 – 26 – 24
3) выражение 22400–24 дает 2396 единиц и 4 нолика в конце, откуда вычеркиваем (заменяем на ноль) единичку, стоящую на седьмом месте справа (26) и, соответственно на 2019 месте справа (22018). Следовательно, остается 2394 единички.
4) С учетом того, что 24032 дает нам одну единицу, в итоге получаем 2395 единиц
5) Ответ: 2395
Ещё пример задания:
Р-15. Решите уравнение 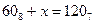 .
.
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
Решение:
1) удобнее всего перевести все числа в десятичную систему, решить уравнение и результат перевести в шестеричную систему
2) получаем 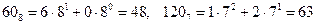
3) уравнение приобретает вид 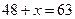 , откуда получаем
, откуда получаем 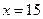
4) переводим 15 в шестеричную систему счисления: 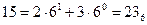
5) ответ: 23.
Решение (программа на Python, А.Н. Носкин):
1) можно (но сложнее) решить задачу с помощью программы:
a = int('60', 8) # перевод "60" в 10-ю систему
b = int('120', 7) # перевод "120" в 10-ю систему
x = b - a # число Х в 10-й системе
x6 = ''
while x > 0:# перевод в 6-ю систему
x6 += str(x%6)
x //= 6
x6 = x6[::-1]# разворот числа
print(x6)
2) ещё один вариант программы (Б.С. Михлин):
x = int('120', 7) - int('60', 8)
print('в 10 c.c:', x)
s = ''
while x:
s = str(x%6) + s
x //= 6
print('Ответ в 6 с.с:', s)
3) ответ: 23.
Ещё пример задания:
Р-14. Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Решение:
1) если запись числа в системе счисления с основанием N заканчивается на 0, то это число делится на N нацело
2) поэтому в данной задаче требуется найти наименьшее натуральное число, которое делится одновременно на 3 и на 5, то есть, делится на 15
3) очевидно, что это число 15.
Решение (программа на Python, А.Н. Носкин):
1) можно (но сложнее) решить задачу с помощью программы:
for i in range(1,100):
x = i
x3 = ''
while x > 0:# перевод в 3-ю систему
x3 += str(x%3)
x //= 3
x3 = x3[::-1][-1]# последняя цифра числа
x = i
x5 = ''
while x > 0:
x5 += str(x%5)
x //= 5
x5 = x5[::-1][-1]
if x3 == "0" and x5 == "0":
print(i)
break
2) ответ: 15.
Решение (программа на Python, Б.С. Михлин):
1) Используется тот факт, что последняя цифра в записи числа в системе счисления с основанием N – это остаток от деления этого числа на N:
for x in range(1,101): # ищем решение от 1 до 100
if x%3 == x%5 == 0: # 'and' можно не использовать
print(x)
break
2) ответ: 15.
Ещё пример задания:
Р-13. Запись числа 6710 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание этой системы счисления N.
Решение:
1) поскольку запись в системе счисления с основанием N заканчивается на 1, то остаток от деления числа 67 на N равен 1, то есть при некотором целом 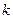 имеем
имеем
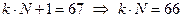
2) следовательно, основание N – это делитель числа 66
3) с другой стороны, запись числа содержит 4 цифры, то есть 
4) выпишем кубы и четвертые степени первых натуральных чисел, которые являются делителями числа 66:
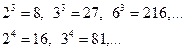
5) видим, что из этого списка только для числа N = 3 выполняется условие 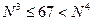
6) таким образом, верный ответ – 3.
7) можно сделать проверку, переведя число 67 в троичную систему 6710 = 21113
Решение (программа на Python, А.Н. Носкин):
1) можно (но сложнее) решить задачу с помощью программы:
for i in range(2,37):# перебираем возможные основания
x = 67
x_N = ''
while x > 0:# перевод в N-ю систему
x_N += str(x%i)
x //= i
x_N = x_N[::-1]# разворот числа
if x_N[-1]== "1" and len(x_N) == 4:
print(i)
break
2) ответ: 3.
Решение (программа на Python, Б.С. Михлин):
1) Если при переводе из 10-й в N-ю систему счисления очередную полученную цифру дописывать слева к найденным ранее цифрам (т.е. так, как мы и делаем при ручном переводе), то не нужен будет разворот числа.
2) Для i > 10 надо учитывать, что цифра может быть буквой.
3) Верхняя граница основания 99 в цикле for i завышена. Арабских цифр и латинских букв хватит только для оснований до 10+26=36. Далее нет общепринятых правил обозначения цифр (если хотим получать N-ичное представление числа).
for N in range(2, 37): # подбираем основание от 2 до 36
x = 67
s = '' # в s будет представление числа в N-ичной системе
while x:
d = x % N # цифра (digit)
if d < 10:
d = str(d) # цифра от 0 до 9
else:
d = chr(ord('A') + d - 10) # «цифра» от A до Z
s = d + s # цифру d приписываем слева к s
x //= N
if s[-1] == '1' and len(s) == 4:
print(N)
break
4) возможен второй вариант: без представления всего числа в N-й системе счисления; здесь можно брать основание больше 36.
for N in range(2, 101): # подбираем основание от 2 до 100
x = 67
k = 0 # счетчик цифр (разрядов) N-ичного числа
while x:
d = x % N # очередная цифра (digit)
k += 1
if k == 1: d0 = d # d0 - младшая цифра
x //= N
if d0 == 1 and k == 4:
print(N)
break
5) ответ: 3.
Еще пример задания:
Р-12. Запись числа 38110 в системе счисления с основанием N оканчивается на 3 и содержит 3 цифры. Укажите наибольшее возможное основание этой системы счисления N.
Решение:
1) поскольку запись в системе счисления с основанием N заканчивается на 3, то остаток от деления числа 381 на N равен 3, то есть при некотором целом 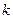 имеем
имеем
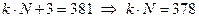
2) следовательно, основание N – это делитель числа 
3) с другой стороны, запись числа содержит 3 цифры, то есть 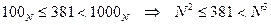
4) неравенство  дает
дает 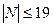 (так как
(так как  )
)
5) неравенство 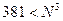 дает
дает 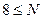 (так как
(так как  )
)
6) таким образом, 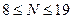 ; в этом диапазоне делителями числа 378 являются числа
; в этом диапазоне делителями числа 378 являются числа
· 9, при  получаем запись числа
получаем запись числа 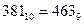
· 14, при 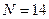 получаем запись числа
получаем запись числа 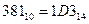
· 18, при  получаем запись числа
получаем запись числа 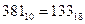
7) наибольшим из приведенных чисел – это 18 (можно было сразу искать подбором наибольший делитель числа 378, начиная с 19 «вниз», на уменьшение)
8) таким образом, верный ответ – 18.
Решение (программа на Python, А.Н. Носкин):
1) можно решить задачу с помощью программы:
for i in range(100,1,-1):# перебираем возможные основания
x = 381
x_N = ''
while x > 0:# перевод в N-ю систему
if x%i>9:break # пропускаем цифры в виде букв
else: x_N += str(x%i)
x //= i
x_N = x_N[::-1]# разворот числа
if x_N == '': pass
elif x_N[-1]== "3" and len(x_N) == 3:
print(i)
break
2) ответ: 18.
Решение (программа на Python, Б.С. Михлин):
1) Если цифры больше девяти не представлять латинскими буквами, то программа даст неверный ответ 27, т.к. 381 в 27-ичной системе не (14)3, а E3 (т.е. двухзначное число)
for N in range(36, 3, -1): # подбираем основание N от 36 до 4
x = 381
s = ''
while x:
d = x % N # цифра (digit)
if d < 10:
d = str(d) # цифра от 0 до 9
else:
d = chr(ord('A') + d - 10) # буквенная цифра от A до Z
s = d + s # цифру d приписываем слева
x //= N
if s[-1] == '3' and len(s) == 3:
print(N)
break
2) ответ: 18.
Еще пример задания:
Р-11. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Общий подход:
· вспомним алгоритм перевода числа из десятичной системы в систему с основанием  (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на
(см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на  , а две младших цифры – это остаток от деления на
, а две младших цифры – это остаток от деления на 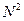 и т.д.
и т.д.
· в данном случае  , остаток от деления числа на
, остаток от деления числа на 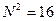 должен быть равен 114 = 5
должен быть равен 114 = 5
· потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16
Решение (вариант 1, через десятичную систему):
1) общий вид чисел, которые дают остаток 5 при делении на 16:
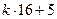
где 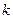 – целое неотрицательное число (0, 1, 2, …)
– целое неотрицательное число (0, 1, 2, …)
2) среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при 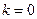 ) и 21 (при
) и 21 (при 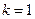 )
)
3) таким образом, верный ответ – 5, 21.
Возможные ловушки и проблемы:
· выражение «не превосходящие 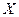 » означает «меньшие или равные » означает «меньшие или равные 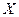 », а не строго меньшие », а не строго меньшие 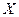 · остаток, состоящий из нескольких цифр (здесь – 114), нужно не забыть перевести в десятичную систему
· найденные числа нужно записать именно в порядке возрастания, как требуется
· остаток, состоящий из нескольких цифр (здесь – 114), нужно не забыть перевести в десятичную систему
· найденные числа нужно записать именно в порядке возрастания, как требуется
|
Решение (вариант 2, через четверичную систему, предложен О.А. Тузовой):
1) переведем 25 в четверичную систему счисления: 25 = 1214, все интересующие нас числа не больше этого значения
2) из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два:
это 114 = 5 и 1114 = 21
3) таким образом, верный ответ – 5, 21.
| Возможные ловушки и проблемы: · есть риск случайно «забыть» какое-то число или найти «лишнее» (в данном случае – большее 25) · можно сделать ошибки при переводе чисел из четверичной системы в десятичную или вообще «забыть» перевести |
Решение (программа на Python, А.Н. Носкин):
1) можно решить задачу с помощью программы:
for i in range(1,31):# перебираем ответы
x = i
x4 = ''
while x > 0:# перевод в 4-ю систему
x4 += str(x%4)
x //=4
x4 = x4[::-1]# разворот числа
if x4[-2:]== "11":
print(i, end=",")
2) ответ: 5, 21.
Решение (программа на Python, Б.С. Михлин):
1) полная программа:
for d in '0', '1': # d - цифра (digit). При d > 1 - выход за 25
# int - переводит из 4-ой в 10-ую систему
print(int(d+'11', 4), end = ',')
2) Ответ: 5, 21.
Еще пример задания:
Р-10. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Общий подход:
· здесь обратная задача – неизвестно основание системы счисления, мы обозначим его через 
· поскольку последняя цифра числа – 2, основание должно быть больше 2, то есть 
· вспомним алгоритм перевода числа из десятичной системы в систему с основанием  (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на
(см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на 
Решение:
1) итак, нужно найти все целые числа 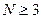 , такие что остаток от деления 23 на
, такие что остаток от деления 23 на  равен 2, или (что то же самое)
равен 2, или (что то же самое)
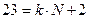 (*)
(*)
где 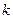 – целое неотрицательное число (0, 1, 2, …);
– целое неотрицательное число (0, 1, 2, …);
2) сложность в том, что и 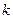 , и
, и  неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
3) из фо