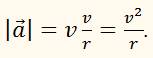Найдём ускорение тела (считаем его материальной точкой), движущегося по окружности с постоянной по модулю скорости.
Ускорение, как известно, определяется по формуле
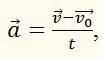
где
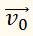
– скорость тела в некоторый начальный момент времени, а
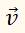
– его скорость через промежуток времени t. Здесь модули скоростей
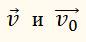
равны друг другу. Предположим, что тело движется по окружности радиусом r и что в некоторый момент времени оно находится в точке А.
Чему равно ускорение в этой точке? Скорость
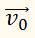
в этой точке направлена по касательной к окружности в точке А. Через t сек тело оказывается в точке В, и скорость его
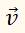
теперь направлена по касательной к окружности в точке В. По модулю скорости
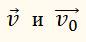
равны (длина стрелок
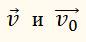
одинаковы).
Надо найти ускорение в точке А окружности (мгновенное ускорение). Поэтому точки А и В, через которые последовательно проходит движущееся тело, надо взять настолько близкими друг к другу, чтобы дуга АВ как бы стянулась в точку.
Определим сначала, как направлено это ускорение.
Проведём из центра О окружности радиусы к точкам А и В. Радиус окружности перпендикулярен к касательной в точке касания, следовательно, радиусы ОА и ОВ перпендикулярны векторам

Чтобы узнать направление вектора ускорения, нужно найти вектор, равный разности векторов

Его направление – это и есть направление вектора ускорения. Чтобы найти разность
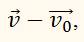
векторы
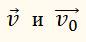
расположим так, чтобы они исходили из одной точки, и соединим их концы, направив стрелку от вычитаемого к уменьшаемому (от конца вектора
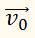
к концу вектора
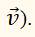
Вектор

и есть разность векторов

Следовательно, вдоль вектора

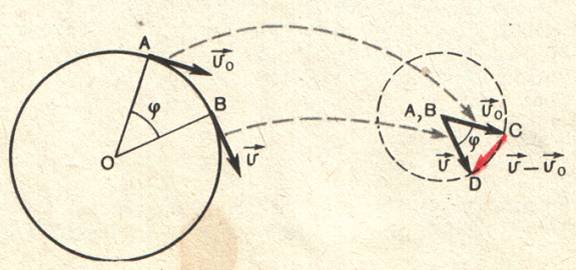
направлено ускорение. Что можно сказать об этом направлении? Треугольник ADC (смотрите рисунок) равнобедренный. Угол при вершине А равен углу φ между радиусами ОА и ОВ (смотрите рисунок), так как они образованы взаимно перпендикулярными сторонами. Точки А и В расположены близко друг к другу, поэтому угол φ очень мал (близок к нулю). Каждый из углов при основании треугольника ADC близок к прямому, так как сумма углов треугольника равна двум прямым. Это означает, что вектор
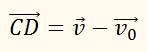
перпендикулярен вектору скорости. Значит, и ускорение перпендикулярно скорости. Но скорость направлена по касательной к окружности в точке А, а касательная перпендикулярна радиусу. Значит, и ускорение направлено по радиусу к центру окружности. Его поэтому называют центростремительным ускорением.
При равномерном движении тела по окружности ускорение в любой её точке перпендикулярно скорости движения и направлено к центру окружности.Эта интересная особенность ускорения при движении по окружности с постоянной по модулю скоростью показана на рисунке.
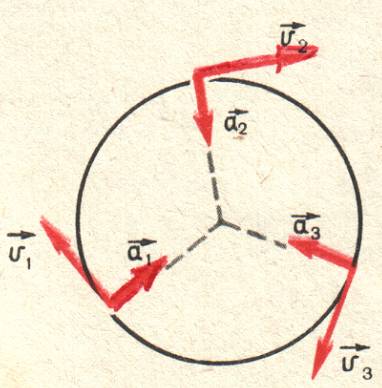
Найдём теперь модуль центростремительного ускорения. Для этого нужно найти, чему равно абсолютное значение величины
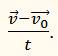
Из рисунка
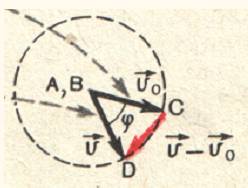
видно, что модуль разности векторов
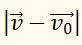
равен длине отрезка CD. Так как угол φ очень мал, то отрезок CD мало отличается от дуги CD окружности (показанной пунктиром) с центром в точке А. Радиус этой окружности r численно равен v (r = v). Но длина такой дуги равна rφ = vφ. Следовательно,
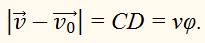
Абсолютное значение ускорения
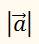
Равно

Но
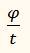
– это угловая скорость ω. Поэтому
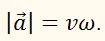
Абсолютное значение ускорения тела, движущегося по окружности, равна произведению его линейной скорости и угловой скорости поворота радиуса, проведённого к телу.
Формулу для центростремительного ускорения удобнее представить в таком виде, чтобы в неё входила величина радиуса окружности, по которой движется тело. Так как угловая и линейная скорости связаны соотношением v = ω r (r – радиус окружности), то подставив это выражение в формулу


получим:
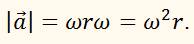
Но
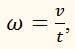
поэтому формулу для центростремительного ускорения можно записать ещё и так: