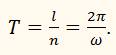ДВИЖЕНИЕ ТОЧКИ ПО ОКРУЖНОСТИ
Составить конспект до выделенного желтым
Прямолинейное движение – это движение, траектория которого - прямая линия, криволинейное – кривая.
Движение тела по окружности является частным случаем криволинейного движения.
Любую кривую можно представить как сумму дуг окружностей разного (или одинакового) радиуса.
Криволинейным движением называют такое движение, которое совершается по дугам окружностей.
Введём некоторые характеристики криволинейного движения.
Криволинейное движение с постоянной по модулю скоростью. Движение с ускорением, т.к. скорость меняет направление.
Угол поворота и угловая скорость.
Движение тела по окружности можно описывать тем же способом, которым пользуются при описании прямолинейного движения. Но часто более удобным оказывается другой способ.
ПРИМЕР:
Представим себе, что некоторое тело движется по окружности радиусом r.
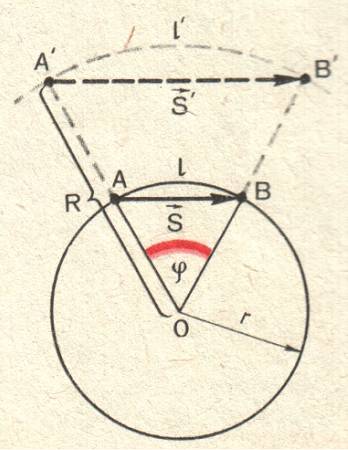
Проведём из центра О окружности радиус к какой-нибудь точке тела А и будем следить не только за самим телом, но и за радиусом, проведённым к нему. Мы увидим, что, по мере того как тело движется, радиус поворачивается. Если, например, тело за промежуток времени t переместилось из точки А в точку В, то за это же время радиус повернулся на угол φ. Этот угол мы будем называть углом поворота радиуса. О движении тела можно, следовательно, сказать, во-первых, что тело за промежуток времени t прошло путь l по дуге АВ окружности, во-вторых, что оно совершило перемещение
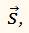
модуль которого равен длине хорды АВ, и, в-третьих, что радиус, проведённый к телу, совершил поворот на угол φ.
Если бы тело двигалось по окружности другого радиуса R ˃ r (смотрите рисунок), то длина пройденного пути была бы больше. Большей была бы и длина перемещения
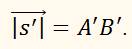
Угол же поворота радиуса в обоих случаях остаётся одними тем же.
ПРИМЕР:
Минутная стрелка маленьких наручных часов за 15 мин проходит путь длиной около 1,5 см. За это же время конец минутной стрелки огромных башенных часов проходит путь длиной в несколько метров. Но минутные стрелки всех часов в мире за четверть часа поворачиваются на один и тот же угол – 90⁰.

Если мы снова вернёмся к рисунку,

то увидим, что у тел, движущихся по окружности с радиусами r и R, равны не только углы поворота. В обоих случаях одинаковы и отношения длины дуги к радиусу:
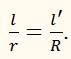
По какой бы окружности ни двигалось тело, при равных углах поворота радиуса равны и отношения длины дуги к радиусу.
Поэтому и сами углы можно измерять величиной этого отношения
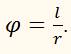
При таком измерении углов за единицу измерения угла удобно принять не градус, а угол, соответствующий дуге, длина которой l равна радиусу r, потому что тогда угол φ будет равен единице. Такая единица измерения называется радианом (сокращённо рад).
Радиан – это угол между двумя радиусами круга, вырезающий на окружности дугу, длина которой равна радиусу.
Установим связь между градусом и радианом.
Когда тело (или точка) совершит один полный оборот по окружности радиусом r, то длина пройденной дуги будет равна 2πr. Поэтому величина угла в радианах равна:
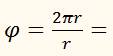
2 π рад ≈ 6,28 рад. Следовательно, один оборот – это поворот радиуса на угол в 2π рад. В градусной мере этот же угол равен 360⁰. Отсюда
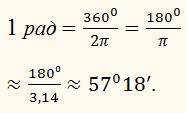
Таким образом, длина дуги, пройденной телом, и угол поворота радиуса, проведённого к нему, связаны формулой
l = rφ.
Скорость равномерного движения тела по окружности тоже можно выражать в угловых единицах. Для этого используют понятие угловой скорости.
Под угловой скоростью мы будем понимать отношение угла
поворота радиуса, проведённого к телу, к промежутку времени, в течении которого совершён этот поворот.
Угловую скорость обозначают греческой буквой ω (омега), так что
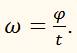
Так как здесь угол φ выражен в радианах, а время t в секундах, то угловая скорость ω измеряется в радианах в секунду (рад/сек). В отличии от угловой скорости скорость v, измеряемую отношением длины пути l ко времени t и выражаемую в метрах в секунду, называют линейной скорость. Между угловой скоростью ω и линейной скоростью v очень простая связь. Если в выражение для угловой скорости подставить вместо φ его значение
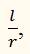
то мы получим:
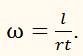
Так как в свою очередь l = vt, то
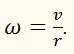
или v = ωr.
Линейная скорость точки равна произведению угловой скорости на радиус окружности, по которой происходит движение.
Скорость движения тела по окружности часто выражают также числом оборотов в единицу времени. Легко связать угловую скорость с числом оборотов в единицу времени. Действительно, при одном обороте радиус поворачивается на угол 2π рад. Значит, совершив в единицу времени, например, n оборотов, радиус повернётся на угол 2πn рад. Поэтому угловая скорость ω и число оборотов в единицу времени n связаны выражением
ω = 2πn.
Число оборотов в единицу времени (n) обычно называют также частотой вращения. Величина, обратная частоте, определяет время, за которое тело делает один оборот. Это время называют периодом вращения и обозначают буквой Т: