ТЕОРИЯ ВЕРОЯТНОСТЕЙ.
| №№ п/п | Понятия, обозначения | Содержание, формула |
| Множество | Множество  – совокупность каких-либо объектов – совокупность каких-либо объектов 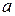 , называемых элементами множества: , называемых элементами множества: 
| |
Дополнение  (не (не  ) )
|  содержит все элементы, не принадлежащие содержит все элементы, не принадлежащие 
| |
Равенство множеств 
| Два множества  и и  равны между собой, если они состоят из одних и тех же элементов равны между собой, если они состоят из одних и тех же элементов
| |
Объединение (сумма) множеств 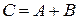
| Множество  состоит из всех элементов, принадлежащих или множеству состоит из всех элементов, принадлежащих или множеству  , или множеству , или множеству 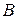 ,или и ,или и  и и 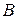 одновременно одновременно
| |
Пересечение (произведение) множеств 
| Множество  состоит из элементов, принадлежащих одновременно и множеству состоит из элементов, принадлежащих одновременно и множеству  и множеству и множеству 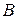
| |
Разность двух множеств 
|  состоит из элементов множества состоит из элементов множества  , которые не являются элементами множества , которые не являются элементами множества 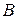
| |
| Эквивалентные множества | Два множества называются эквивалентными, если между ними установлено взаимно-однозначное соответствие. | |
| Счетные множества | Бесконечные множества, эквивалентные множеству натуральных чисел 
| |
| Перестановки. Число перестановок | Соединения, отличающиеся только порядком элементов, называются перестановками. Число перестановок из  элементов элементов 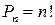 , где , где
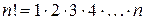

| |
| Размещения. Число размещений | Соединения из  различных элементов по различных элементов по  , отличающихся друг от друга составом элементов либо их порядком, называются размещениями. Число размещений из , отличающихся друг от друга составом элементов либо их порядком, называются размещениями. Число размещений из  по по 

|
| Сочетания. Число сочетаний | Соединения из  различных элементов по различных элементов по  , отличающихся друг от друга хотя бы одним элементом, называются сочетаниями. Число сочетаний из , отличающихся друг от друга хотя бы одним элементом, называются сочетаниями. Число сочетаний из  по по 
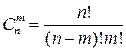
 ; ;
 ; ; 

| |
| Стохастический эксперимент | Это опыт (испытание), результат которого заранее не определен | |
| Достоверное событие | Результат, который обязательно наступает при осуществлении данного комплекса условий (опыта, эксперимента) называется достоверным событием | |
| Случайное событие | Это событие, которое может произойти, а может и не произойти в данном испытании | |
| Невозможное событие | Это событие, которое не может произойти при данном комплексе условий | |
Относительная частота события 
| Отношение 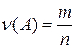 числа экспериментов числа экспериментов  , завершившихся событием , завершившихся событием  , к общему числу , к общему числу  проведенных экспериментов проведенных экспериментов
| |
| Статистическое определение вероятности | Если при неограниченном увеличении числа экспериментов относительная частота события  стремится к некоторому фиксированному числу, то событие стремится к некоторому фиксированному числу, то событие  стохастически устойчиво и это число стохастически устойчиво и это число  называют вероятностью события называют вероятностью события 
| |
| Определение вероятности в классической схеме |  , где , где  – число исходов стохастического эксперимента, благоприятствующих наступлению события – число исходов стохастического эксперимента, благоприятствующих наступлению события  , ,  – общее число всех равновозможных исходов – общее число всех равновозможных исходов
|
Вероятность суммы (объединения), двух событий  и и 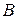
|  
| |
Вероятность произведения двух зависимых событий  и и 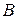
| 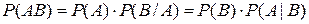 ,
где ,
где  – условная вероятность события – условная вероятность события 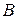 при условии, что событие при условии, что событие  с ненулевой вероятностью произошло с ненулевой вероятностью произошло
| |
Независимые события  и и 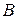
| Это такие события, для которых  и и  .
Следовательно, .
Следовательно, 
| |
| Схема Бернулли | Стохастический эксперимент состоит из последовательности  независимых и одинаковых испытаний, в каждом из которых может произойти событие независимых и одинаковых испытаний, в каждом из которых может произойти событие  или событие, ему противоположное или событие, ему противоположное  с вероятностями соответственно равными с вероятностями соответственно равными 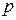 и и 
| |
| Формула Бернулли | Вероятность того, что в серии из  испытаний событие испытаний событие  появится ровно появится ровно  раз раз 
| |
Вероятность того, что при  испытаниях испытаниях  появляется не менее появляется не менее  и не более и не более  раз вычисляется по формуле: раз вычисляется по формуле:

| ||
| Формула Пуассона | При достаточно большом  и малом и малом 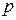 (если (если  (таблица 1) (таблица 1)
| |
 (таблица 2) (таблица 2)
| ||
| Локальная формула Муавра-Лапласа | При достаточно большом  и не слишком малых и не слишком малых 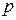 и и 
 , где , где  и и 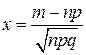 ; ;  (таблица 3) (таблица 3)
|
| Интегральная формула Муавра – Лапласа | 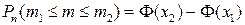 ,
где ,
где  ; ;  ; ;  ; ;  (таблица 4) (таблица 4)
| |
| Понятие случайной величины | Случайной величиной называют переменную величину, которая принимает числовые значения в зависимости от исходов испытания случайным образом. | |
Понятие дискретной случайной величины (ДСВ 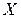 ) )
| ДСВ  – случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, то есть численные значения которой образуют конечное или счетное множество. – случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, то есть численные значения которой образуют конечное или счетное множество.
| |
| Закон распределения дискретной случайной величины | Соответствие между значениями  дискретной случайной величины и их вероятностями дискретной случайной величины и их вероятностями  называется законом распределения и может быть задан таблично или аналитически (то есть с помощью формул). Если ДСВ называется законом распределения и может быть задан таблично или аналитически (то есть с помощью формул). Если ДСВ  принимает конечное множество значений принимает конечное множество значений   соответственно с вероятностями соответственно с вероятностями  , то ее закон распределения определяется формулами , то ее закон распределения определяется формулами
 , ,  и и  Если ДСВ
Если ДСВ  принимает бесконечную последовательность значений принимает бесконечную последовательность значений  соответственно с вероятностями соответственно с вероятностями 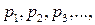 , то ее закон распределения определяется формулами , то ее закон распределения определяется формулами
 , ,  и и 
|
Понятие непрерывной случайной величины (НСВ  ) )
| НСВ  – случайная величина, которая может принимать любые значения из некоторого промежутка, то есть множество значений непрерывной случайной величины несчетно. – случайная величина, которая может принимать любые значения из некоторого промежутка, то есть множество значений непрерывной случайной величины несчетно.
| |
| Функция распределения. Свойства функции распределения | Функцией распределения случайной величины  называется функция действительного переменного называется функция действительного переменного  , определяемая равенством , определяемая равенством  , где , где  - вероятность того, что случайная величина - вероятность того, что случайная величина  принимает значение, меньше принимает значение, меньше  .
Функция распределения .
Функция распределения  для ДСВ для ДСВ  , которая может принимать значения , которая может принимать значения   c соответствующими вероятностями c соответствующими вероятностями  имеет вид имеет вид  , где символ , где символ  означает, что суммируются вероятности означает, что суммируются вероятности  тех значений, которые меньше тех значений, которые меньше  .
Функция является разрывной.
Случайная величина .
Функция является разрывной.
Случайная величина  называется непрерывной, если ее функция распределения называется непрерывной, если ее функция распределения  является непрерывно дифференцируемой.
Вероятность того, что СВХ примет значение из промежутка является непрерывно дифференцируемой.
Вероятность того, что СВХ примет значение из промежутка  , равна разности значений ее функции распределения на концах этого полуинтервала: , равна разности значений ее функции распределения на концах этого полуинтервала:
 Свойства функции распределения
1.
Свойства функции распределения
1.  2. Если
2. Если  , то , то  , то есть функция распределения является неубывающей. , то есть функция распределения является неубывающей.
|
| Функция распределения. Свойства функции распределения | 3. Функция  в точке в точке  непрерывна слева, то есть непрерывна слева, то есть  ; ;  4. Если все возможные значения СВХ принад-лежат интервалу
4. Если все возможные значения СВХ принад-лежат интервалу 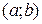 , то , то  при при  , ,
 при при  5. Если все возможные значения СВХ принад-лежат бесконечному интервалу
5. Если все возможные значения СВХ принад-лежат бесконечному интервалу  , то , то
 ;
Если ;
Если  – непрерывная случайная величина, то вероятность того, что она примет одно заданное определенное значение, равна нулю: – непрерывная случайная величина, то вероятность того, что она примет одно заданное определенное значение, равна нулю:
 Отсюда следует, что для непрерывной случайной величины выполняются равенства:
Отсюда следует, что для непрерывной случайной величины выполняются равенства:


| |
| Плотность распределения вероятностей непрерывной случайной величины. Свойства функции плотности распределения. | Плотностью распределения (дифференциальной функцией распределения) вероятностей НСВ  в точке в точке  называют предел отношения вероятности попадания значений этой величины в интервал называют предел отношения вероятности попадания значений этой величины в интервал  к длине к длине  этого интервала, когда последняя стремится к нулю: этого интервала, когда последняя стремится к нулю:
 Следовательно,
Следовательно, 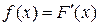 , то есть плотность распределения есть первая производная от функции распределения НСВХ.
Вероятность того, что НСВХ примет значение, принадлежащее интервалу , то есть плотность распределения есть первая производная от функции распределения НСВХ.
Вероятность того, что НСВХ примет значение, принадлежащее интервалу  , определяется равенством , определяется равенством 
|
| Плотность распределения вероятностей непрерывной случайной величины. Свойства функции плотности распределения. | Зная плотность распределения, можно найти функцию распределения  Свойства функции плотности
1. Плотность распределения
Свойства функции плотности
1. Плотность распределения  - неотрицательная функция, то есть - неотрицательная функция, то есть  2. Несобственный интеграл по бесконечному промежутку
2. Несобственный интеграл по бесконечному промежутку  от функции плотности вероятностей равен единице: от функции плотности вероятностей равен единице:  3. Если все возможные значения случайной величины принадлежат отрезку
3. Если все возможные значения случайной величины принадлежат отрезку  , то , то  , так как вне этого промежутка , так как вне этого промежутка 
| |
| Математическое ожидание | Для ДСВ  равно сумме произведений всех ее значений на соответствующие вероятности: равно сумме произведений всех ее значений на соответствующие вероятности:  Для НСВ
Для НСВ  ,
где ,
где 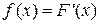 – функция плотности распределения вероятности. – функция плотности распределения вероятности.
| |
| Свойства математического ожидания | 1)  , если , если  2)
2) 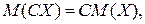 3)
3)  4) Если
4) Если  и и  – независимые случайные величины, то – независимые случайные величины, то 
|
| Дисперсия случайной величины | Разность  называется отклонением случайной величины называется отклонением случайной величины  от ее математического ожидания от ее математического ожидания  .
Математическое ожидание отклонения равно нулю: .
Математическое ожидание отклонения равно нулю:  Дисперсией, или рассеянием случайной величины
Дисперсией, или рассеянием случайной величины  называется математическое ожидание квадрата ее отклонения: называется математическое ожидание квадрата ее отклонения:
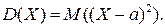 Следовательно, для любой случайной величины Следовательно, для любой случайной величины 
| |
| Свойства дисперсии | 1)  , ,  2)
2)  , ,  3) Если случайные величины
3) Если случайные величины  и и 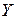 независимы, то независимы, то 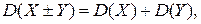 4)
4)  5)
5) 
| |
| Среднее квадратическое отклонение | Среднеквадратическим отклонением, или стандартным отклонением, случайной величины  называется корень квадратный из ее дисперсии: называется корень квадратный из ее дисперсии:
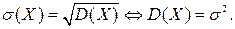
| |
| Биномиальное распределение | Закон распределения дискретной случайной величины, определяемой формулой Бернулли
 называется биномиальным. Постоянные
называется биномиальным. Постоянные  , , 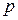 называются параметрами биномиального распределения называются параметрами биномиального распределения 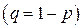 . .

| |
| Распределение Пуассона | Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой Пуассона 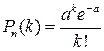 , где , где 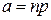 – параметр распределения. – параметр распределения.
 . .
|
Равномерное распределение на интервале 
| Если значения случайной величины, которые она принимает в конечном промежутке  , возможны в одинаковой степени, то плотность распределения вероятностей этой величины постоянна на данном промежутке и равна нулю вне этого промежутка, то есть , возможны в одинаковой степени, то плотность распределения вероятностей этой величины постоянна на данном промежутке и равна нулю вне этого промежутка, то есть
 Доказано, что
Доказано, что 
 ; ;  ; ; 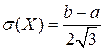
| |
| Геометрическое распределение | Геометрическим называется распределение дискретной случайной величины  , определяемое формулой , определяемое формулой
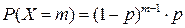 , где , где  , и , и  (Вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем (Вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем 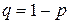 ). ).
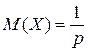 ; ; 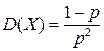
| |
| Показательное распределение | Показательным называется распределение с плотностью вероятностей, определяемой по формуле  где
где  - параметр распределения. - параметр распределения.
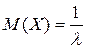 ; ;  ; ; 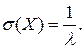 Замечание. Если
Замечание. Если  – время безотказной работы элемента, – время безотказной работы элемента,  - интенсивность отказов, то случайная величина - интенсивность отказов, то случайная величина  распределена по экспоненциальному закону с функцией распределения распределена по экспоненциальному закону с функцией распределения  где где 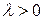 . .  определяет вероятность отказа элемента за время определяет вероятность отказа элемента за время  . Вероятность безотказной работы элемента за время . Вероятность безотказной работы элемента за время  равна равна  . Функция . Функция 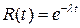 называется функцией надежности. называется функцией надежности.
|
Нормальное распределение 
| Нормальным распределением, или распределением Гаусса, называется распределение с плотностью вероятностей
 Постоянные
Постоянные  и и   называются параметрами нормального распределения. называются параметрами нормального распределения.
 ; ;  ; ;  Вероятность попадания значений нормальной случайной величины
Вероятность попадания значений нормальной случайной величины  в интервале в интервале  определяется формулой определяется формулой
 где
где  – функция Лапласа. – функция Лапласа.
 ; ; 
| |
Нормированное распределение 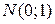
| Нормированным или стандартным называется такое нормальное распределение непрерывной случайной величины, когда функция плотности вероятностей 
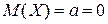 ; ; 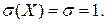
| |
Мода случайной величины 
| Модой ДСВ  называется ее наиболее вероятное значение.
Модой НСВ называется ее наиболее вероятное значение.
Модой НСВ  называется то ее значение, при котором плотность распределения вероятностей максимальна. называется то ее значение, при котором плотность распределения вероятностей максимальна.
| |
Медиана 
| Медианой непрерывной случайной величины  называется такое ее значение называется такое ее значение  , для которого одинаково вероятно, окажется ли случайная величина меньше или больше , для которого одинаково вероятно, окажется ли случайная величина меньше или больше  , то есть , то есть  .
Если прямая .
Если прямая  является осью симметрии кривой распределения является осью симметрии кривой распределения  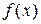 , то , то
 . .
|
Начальные моменты 
| Начальным моментом  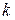 -го порядка случайной величины -го порядка случайной величины  называется математическое ожидание называется математическое ожидание 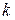 -ой степени этой случайной величины: -ой степени этой случайной величины:  .
Для ДСВ .
Для ДСВ   , где , где  .
Начальный момент .
Начальный момент 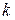 -го порядка НСВ Х с плотностью распределения -го порядка НСВ Х с плотностью распределения 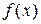 определяется формулой: определяется формулой:
 , где , где  . .
| |
Центральные моменты 
| Центральным моментом  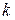 -го порядка случайной величины -го порядка случайной величины  называется математическое ожидание называется математическое ожидание 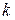 -ой степени отклонения этой величины от ее математического ожидания. Если обозначить -ой степени отклонения этой величины от ее математического ожидания. Если обозначить  , то , то  Для ДСВ
Для ДСВ   ,
если множество этой величины конечно, а если – счетно, то ,
если множество этой величины конечно, а если – счетно, то  Для НСВ
Для НСВ  с плотностью распределения с плотностью распределения 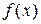 центральный момент центральный момент 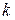 -го порядка опре-деляется формулой: -го порядка опре-деляется формулой: 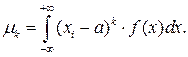
| |
| Некоторые свойства начальных и центральных моментов |  ; ; 
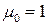 ; ;  ; ; 

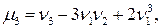

|
| Асимметрия | Отношение центрального момента 3-го порядка к кубу среднеквадратического отклонения случайной величины называется асимметрией:  .
Если распределение случайной величины симметрично относительно ее математического ожидания, то асимметрия равна нулю. .
Если распределение случайной величины симметрично относительно ее математического ожидания, то асимметрия равна нулю.
| |
| Эксцесс | Эксцессом случайной величины называется величина 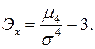 Для нормального распределения
Для нормального распределения 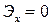 .
Кривые, более островершинные по сравнению с нормальной кривой Гаусса, имеют .
Кривые, более островершинные по сравнению с нормальной кривой Гаусса, имеют  . У более плосковершинных кривых . У более плосковершинных кривых 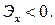
|
ПРИЛОЖЕНИЯ
Таблица П.1
Значения функции 
| а m | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 |
| 0,9048 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5488 | |
| 0,0905 | 0,0,2222 | 0,2681 | 0,3033 | 0,3293 | ||
| 0,0045 | 0,0164 | 0,0333 | 0,0536 | 0,0758 | 0,0988 | |
| 0,0002 | 0,0011 | 0,0033 | 0,0072 | 0,0126 | 0,0198 | |
| 0,0001 | 0,0002 | 0,0007 | 0,0016 | 0,0030 | ||
| 0,0001 | 0,0002 | 0,0004 | ||||
| а m | 0,7 | 0,8 | 0,9 | 1,0 | 2,0 | 3,0 |
| 0,4966 | 0,4493 | 0,4066 | 0,3679 | 0,1353 | 0,0498 | |
| 0,3476 | 0,3595 | 0,3659 | 0,3679 | 0,2707 | 0,1494 | |
| 0,1217 | 0,1438 | 0,1647 | 0,1839 | 0,2707 | 0,2240 | |
| 0,0284 | 0,0383 | 0,0494 | 0,0613 | 0,1804 | 0,2240 | |
| 0,0050 | 0,0077 | 0,0111 | 0,0153 | 0,0902 | 0,1680 | |
| 0,0007 | 0,0,0012 | 0,0020 | 0,0031 | 0,0361 | 0,1008 | |
| 0,0001 | 0,0002 | 0,0003 | 0,0005 | 0,0120 | 0,0504 | |
| 0,0001 | 0,0034 | 0,0216 | ||||
| 0,0009 | 0,0081 | |||||
| 0,0002 | 0,0027 | |||||
| 0,0008 | ||||||
| 0,0002 | ||||||
| 0,0001 | ||||||
| а m | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 |
| 0,0183 | 0,0067 | 0,0025 | 0,0009 | 0,0003 | 0,0001 | |
| 0,0733 | 0,0337 | 0,0149 | 0,0064 | 0,0027 | 0,0011 | |
| 0,1465 | 0,0446 | 0,0223 | 0,0107 | 0,0050 | ||
| 0,1954 | 0,1404 | 0,0892 | 0,0521 | 0,0286 | 0,0150 | |
| 0,1954 | 0,1755 | 0,1339 | 0,0912 | 0,0572 | 0,0337 | |
| 0,1563 | 0,1755 | 0,1606 | 0,1277 | 0,0916 | 0,0607 | |
| 0,1042 | 0,1462 | 0,1606 | 0,1490 | 0,1221 | 0,0911 | |
| 0,0595 | 0,1044 | 0,1377 | 0,1490 | 0,1396 | 0,1171 | |
| 0,0298 | 0,0653 | 0,1033 | 0,1304 | 0,1396 | 0,1318 | |
| 0,0132 | 0,0363 | 0,0688 | 0,1014 | 0,1241 | 0,1318 | |
| 0,0053 | 0,0181 | 0,0413 | 0,0710 | 0,0993 | 0,1186 | |
| 0,0019 | 0,0082 | 0,0225 | 0,0452 | 0,0722 | 0,0970 | |
| 0,0006 | 0,0034 | 0,0113 | 0,0264 | 0,0481 | 0,0728 | |
| 0,0002 | 0,0013 | 0,0052 | 0,0142 | 0,0296 | 0,0504 | |
| 0,0001 | 0,0005 | 0,0022 | 0,0071 | 0,0169 | 0,0324 | |
| 0,0022 | 0,0009 | 0,0033 | 0,0090 | 0,0194 | ||
| 0,0001 | 0,0003 | 0,0015 | 0,0045 | 0,0109 | ||
| 0,0001 | 0,0006 | 0,0021 | 0,0058 | |||
| 0,0002 | 0,0009 | 0,0029 | ||||
| 0,0004 | 0,0014 | |||||
| 0,0002 | 0,0006 | |||||
| 0,0001 |
Таблица П.2
Значения функции 
| а k | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 |
| 0,9048 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5488 | |
| 0,9953 | 0,9825 | 0,9631 | 0,9384 | 0,9098 | 0,8781 | |
| 0,9998 | 0,9989 | 0,9964 | 0,9921 | 0,9856 | 0,9769 | |
| 1,0000 | 0,9999 | 0,9997 | 0,9992 | 0,9983 | 0,9966 | |
| 1,0000 | 1,0000 | 0,9999 | 0,9998 | 0,9996 | ||
| 1,0000 | 1,0000 | 1,0000 | ||||
| а k | 0,7 | 0,8 | 0,9 | 1,0 | 2,0 | 3,0 |
| 0,4966 | 0,4493 | 0,4066 | 0,3679 | 0,1353 | 0,0498 | |
| 0,8442 | 0,8088 | 0,7725 | 0,7358 | 0,4060 | 0,1991 | |
| 0,9659 | 0,9526 | 0,9371 | 0,9197 | 0,6767 | 0,4232 | |
| 0,9942 | 0,9909 | 0,9865 | 0,9810 | 0,8571 | 0,6472 | |
| 0,9992 | 0,9986 | 0,9977 | 0,9963 | 0,9473 | 0,8153 | |
| 0,9999 | 0,9998 | 0,9997 | 0,9994 | 0,9834 | 0,9161 | |
| 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9955 | 0,9665 | |
| 1,0000 | 0,9989 | 0,9881 | ||||
| 0,9998 | 0,9962 | |||||
| 1,0000 | 0,9989 | |||||
| 0,9997 | ||||||
| 0,999 | ||||||
| 1,0000 | ||||||
| а k | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 |
| 0,0183 | 0,0067 | 0,0025 | 0,0009 | 0,0003 | 0,0001 | |
| 0,0916 | 0,0404 | 0,0174 | 0,0073 | 0,0030 | 0,0012 | |
| 0,2381 | 0,1247 | 0,0620 | 0,0296 | 0,0138 | 0,0062 | |
| 0,4335 | 0,2650 | 0,1512 | 0,0818 | 0,0424 | 0,0212 | |
| 0,6288 | 0,4405 | 0,2851 | 0,1730 | 0,0996 | 0,0550 | |
| 0,7851 | 0,6160 | 0,4457 | 0,3008 | 0,1912 | 0,1157 | |
| 0,8893 | 0,7622 | 0,6063 | 0,4497 | 0,3133 | 0,2068 | |
| 0,9489 | 0,8666 | 0,7440 | 0,5987 | 0,4530 | 0,3239 | |
| 0,9786 | 0,9318 | 0,8472 | 0,7291 | 0,5925 | 0,4557 | |
| 0,9919 | 0,9682 | 0,9161 | 0,8305 | 0,7166 | 0,5874 | |
| 0,9972 | 0,9863 | 0,9574 | 0,9015 | 0,8159 | 0,7060 | |
| 0,9991 |
|
| Поделиться: |
Поиск по сайту
©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2019-04-14 Нарушение авторских прав и Нарушение персональных данных
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2019-04-14 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд