Цель работы: обобщить и систематизировать умения решать неравенства различного типа методом интервалов.
Теоретические сведения к практической работе:
Пусть заданное неравенство имеет вид: 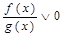 . Для решения этого неравенства используется так называемый метод интервалов, который состоит в следующем.
. Для решения этого неравенства используется так называемый метод интервалов, который состоит в следующем.
1. На числовую ось наносят точки х 1,, х n разбивающие ее на промежутки, в которых выражение 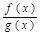 определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений
определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений 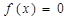 и
и 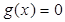 . Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками – точки, удовлетворяющие заданному неравенству, а светлыми кружками – не удовлетворяющие ему.
. Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками – точки, удовлетворяющие заданному неравенству, а светлыми кружками – не удовлетворяющие ему.
2. Определяют и отмечают на числовой оси знак выражения 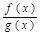 для значений
для значений  , принадлежащих каждому из полученных промежутков. Достаточно определить знак функции
, принадлежащих каждому из полученных промежутков. Достаточно определить знак функции 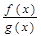 в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.
в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.
Изменение знаков удобно иллюстрировать с помощью волнообразной кривой (кривой знаков), проведенной через отмеченные точки и лежащей выше или ниже числовой оси в соответствии со знаком дроби 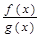 в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству:
в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству:
Пример 1. Решите неравенство: 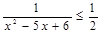 .
.
Решение: упрощаем неравенство путем равносильных преобразований: при умножении или делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный: 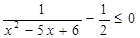 .
.
Приведем дроби к общему знаменателю:
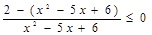 ,
,
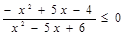 ,
,
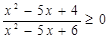
Выражения, стоящие в числителе и знаменателе, можно разложить на множители, тогда неравенство примет вид: 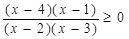 .
.
Далее находим корни уравнений 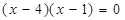 и
и 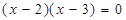 .
.
Из первого получаем х 1=4, х 2=1. Из второго получаем х 3=2, х 4=3.
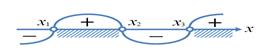
Наносим на числовую прямую получившиеся точки, причем точки х 1, х 2 обозначаем закрашенными кружочками (для них неравенство выполняется), а точки х 3, х 4 светлыми (при этих значениях, выражение, стоящее слева от знака неравенства, не имеет смысла).
Определяем теперь знаки выражения 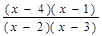 на полученных промежутках (подставляем любое значение х из каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется:
на полученных промежутках (подставляем любое значение х из каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется: 
Кривая знаков выражения 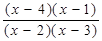
Итак, исходному неравенству удовлетворяют следующие значения: х Є(-∞; 1]U(2; 3)U[4; +∞).
Пример 2. Решите неравенство: 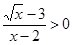 .
.
Решение: подкоренное выражение, как известно, не может принимать отрицательных значений, также не допускается нахождение в знаменателе дроби нуля. Следовательно, область допустимых значений данного неравенства определяется неравенством 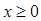 и тем условием, что
и тем условием, что 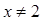 .
.
Решаем уравнения 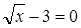 и
и 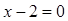 .
.
Из первого уравнения получаем, что х 1=9.
Из второго уравнения получаем, что х 2=2.
Наносим область допустимых значений неравенства и полученные точки на числовую прямую, причем эти точки будут светлыми, поскольку ни одно из значений не удовлетворяет неравенству. Сразу определяем знаки выражения 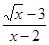 в каждом из полученных промежутков и рисуем кривую знаков:
в каждом из полученных промежутков и рисуем кривую знаков: 
Кривая знаков выражения 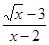
Верхней стрелкой на рисунке обозначена область допустимых значений неравенства. Ответом к неравенству будет являться промежуток, соответствующий на рисунке заштрихованной области.
Ответ: х Є[0; 2)U(9; +∞).
Задания для самостоятельного решения:
1. Решите неравенство: 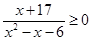 .
.
2. Решите неравенство: 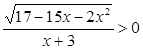 .
.
3. Решите неравенство: 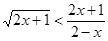 .
.
Контрольные вопросы:
1. Дайте определение неравенства с одной переменной.
2. В чем суть метода интервалов?
Практическая работа «Решение прикладных задач»
Цель работы: обобщить и закрепить знания и умения решать прикладные задачи по определенной схеме.
Теоретические сведения к практической работе:
Прикладными задачами называются задача, решение которых имеет практическое значение (т. е. их можно реально применить для чего-либо).
Прикладные задачи сводятся к решению по определенной схеме.
Движение:
V (скорость) ∙ t (время) = S (расстояние)
Работа:
р (производительность) ∙ t (время) = А (работа)
Покупка:
Цена ∙ Количество = Стоимость
То есть действия с выражениями аналогичные.
А теперь можно перейти к непосредственным примерам решения задач по алгоритму: 1. Прочитать весь текст задачи;
2. Определить ее тип, исходя из условия;
3. Составить таблицу;
4. Заполнить таблицу, читая каждое предложение условия задачи;
5. Найти в таблице место вопросу задачи.
1. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Ответ: 72 км/ч
2. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Решение. Важно объяснить, что в отличие от задачи 1, придорожный столб зафиксирован. Поезд за 36 с проезжает расстояние, равное собственной длине, со скоростью 80 км/ч = 80 * 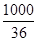 (м/с) = (м/с) = 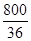 (м/с). Длина поезда (м/с). Длина поезда 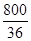 * 36 = 800 (м).
Ответ: 800 м
3. Дальнобойщик, погрузив груз в фуру, отправился в путь со скоростью 60 км/ч. Через 1 ч он сделал остановку на заправке на 30 мин, а затем продолжил путь с первоначальной скоростью. Через 1 ч после отправки фуры диспетчер склада обнаружил, что он забыл отдать дальнобойщику сопроводительные документы на груз и выехал вдогонку на мотоцикле со скоростью 100 км/ч. Какое расстояние (в километрах) проедет мотоциклист до места встречи?
Решение. Задачи на движение вдогонку встречаются часто. Собака догоняет шляпу, унесенную ветром, ребенок проезжает на велосипеде путь, возвращаясь от конечной точки до равномерно движущихся вслед за ним родителей и т. д.
В данной задаче путь дальнобойщика равен пути мотоциклиста. Важно не забыть, что дальнобойщик двигался (1+х–0,5) часа, где х ч – время движения мотоциклиста. Решив уравнение 60(х + 0,5) = 100х, х = 0,75, найдем путь мотоциклиста, который равен 75 км.
Ответ: 75 км
4.Катер проплывает 20 км против течения реки и еще 24 км по течению за то же время, за какое может проплыть по этой реке 9 км. Во сколько раз скорость катера больше скорости реки?
Решение. Как и в задаче 5, не нужно стремиться найти скорости катера и течения реки. Необходимо вычислить отношение * 36 = 800 (м).
Ответ: 800 м
3. Дальнобойщик, погрузив груз в фуру, отправился в путь со скоростью 60 км/ч. Через 1 ч он сделал остановку на заправке на 30 мин, а затем продолжил путь с первоначальной скоростью. Через 1 ч после отправки фуры диспетчер склада обнаружил, что он забыл отдать дальнобойщику сопроводительные документы на груз и выехал вдогонку на мотоцикле со скоростью 100 км/ч. Какое расстояние (в километрах) проедет мотоциклист до места встречи?
Решение. Задачи на движение вдогонку встречаются часто. Собака догоняет шляпу, унесенную ветром, ребенок проезжает на велосипеде путь, возвращаясь от конечной точки до равномерно движущихся вслед за ним родителей и т. д.
В данной задаче путь дальнобойщика равен пути мотоциклиста. Важно не забыть, что дальнобойщик двигался (1+х–0,5) часа, где х ч – время движения мотоциклиста. Решив уравнение 60(х + 0,5) = 100х, х = 0,75, найдем путь мотоциклиста, который равен 75 км.
Ответ: 75 км
4.Катер проплывает 20 км против течения реки и еще 24 км по течению за то же время, за какое может проплыть по этой реке 9 км. Во сколько раз скорость катера больше скорости реки?
Решение. Как и в задаче 5, не нужно стремиться найти скорости катера и течения реки. Необходимо вычислить отношение 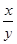 , где х км/ч – собственная скорость катера, у км/ч – скорость течения реки. Уравнение , где х км/ч – собственная скорость катера, у км/ч – скорость течения реки. Уравнение 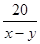 + + 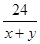 = = 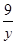 после преобразований примет вид: 5у² + 44 ху – 9х² = 0. Разделив обе части уравнения на у² ≠ 0 и обозначив после преобразований примет вид: 5у² + 44 ху – 9х² = 0. Разделив обе части уравнения на у² ≠ 0 и обозначив 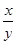 = m, имеем 9m² - 44m – 5 = 0. m1 = 5, m2 = - = m, имеем 9m² - 44m – 5 = 0. m1 = 5, m2 = - 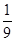 – не соответствует условию задачи. В 5 раз скорость катера больше скорости реки.
Ответ: в 5 раз
Задания для самостоятельного решения:
1. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
2. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
3.Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
4.Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
Контрольные вопросы:
1. Какие задачи являются прикладными?
2. По какой схеме можно решать прикладные задачи?
Практическая работа «Преобразование выражений, содержащих корень» – не соответствует условию задачи. В 5 раз скорость катера больше скорости реки.
Ответ: в 5 раз
Задания для самостоятельного решения:
1. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
2. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
3.Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
4.Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
Контрольные вопросы:
1. Какие задачи являются прикладными?
2. По какой схеме можно решать прикладные задачи?
Практическая работа «Преобразование выражений, содержащих корень»
|
Цель работы: повторить и обобщить умения вычислять корень разной степени и применение этих действий для преобразования выражений содержащих корень
Теоретические сведения к практической работе:
Определение: Арифметическим корнем натуральной степени п ≥ 2 из неотрицательного числа а называется
неотрицательное число, п – ая степень которого равна а.
Примеры
1. 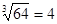 , так как 4 > 0 и 43 = 64 2.
, так как 4 > 0 и 43 = 64 2. 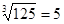 , так как 5 > 0 и 53 = 125
, так как 5 > 0 и 53 = 125
Из определения арифметического корня следует, что если а ≥ 0, то 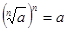 и
и 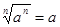
Свойства арифметического корня:
Арифметический корень п – ой степени обладает следующими свойствами: если а ≥ 0, b ≥ 0 и п, т - натуральные числа, причём п ≥ 2, т ≥ 2, то
1. 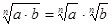 2.
2. 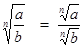
3. 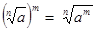 4.
4. 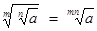
Корень нечётной степени из отрицательного числа а вычисляется следующим образом:
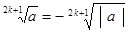
Например, 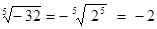
Примеры применения свойств арифметического корня.
1. 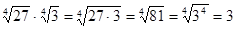
2. 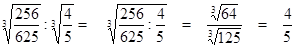
3. 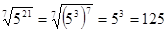
4. 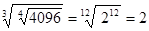
5. 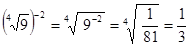
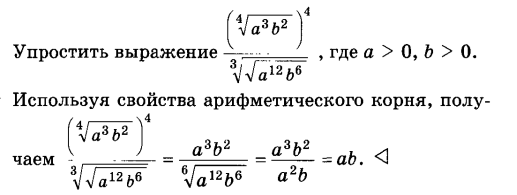
Задания для самостоятельного решения:
1 вариант
1. Вычислить: а) 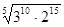

 ; б)
; б) 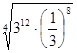
2. Упростить выражение: а) 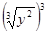 ; б)
; б) 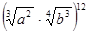 ;
;
3. Вычислить: а) 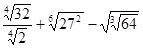 ; б)
; б) 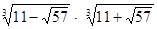 ; в)
; в) 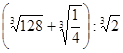
4. Упростить выражение: 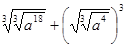
2 вариант
1. Вычислить: а) 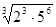
 б)
б) 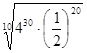
2. Упростить выражение:; а) 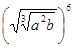 ; б)
; б) 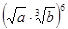
3. Вычислить: а) 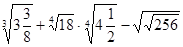 ; б)
; б) 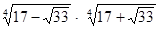 ; в)
; в) 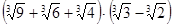
4. Упростить выражение: 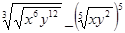
Контрольные вопросы:
1. Что такое арифметический корень?
2. Какие основные свойства арифметического корня?