Практические работы по разделу «Уравнения и неравенства»
Практическая работа «Решение иррациональных уравнений»
Цель работы: Обобщить и систематизировать знания по теме «иррациональные уравнения». Закрепить умения использовать полученные знания для решения уравнений
Теоретические сведения к практической работе:
Для решения рационального уравнения используем последовательно знания следующих свойств:
- Стандартные приемы: раскрытие скобок.
- Методы решения уравнений: введение новой переменной.
- Правила преобразования уравнений.
- Решение квадратного уравнения.
Уравнение, которые можно свести к дроби f(x)/g(x)=0, называется дробно рациональным уравнением. Если уравнение имеет несколько слагаемых, то переносим их по одну сторону знака равенства и сводим к общему знаменателю. В результате получим дробную функцию f(x)/g(x), которая равна нулю 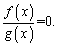
Следующим шагом находим корни числителя. Отвергаем среди них те, которые не принадлежат области допустимых значений (нули знаменателя) и записываем правильный ответ.
Иррациональным называется уравнение, в котором неизвестное (переменная) содержится под знаком корня или под знаком операции возведения в рациональную (дробную) степень.
Для решения иррациональных уравнений обычно используются следующие приемы:
1) «уединение» корня в одной из частей уравнения и возведение в соответствующую степень;
2) введение новой переменной;
3) сведение к системе уравнений;
4) применение свойств функций, входящих в уравнение.
Следует помнить, что при решении иррациональных уравнений необходима проверка всех найденных корней путем их подстановки в исходное уравнение или нахождение ОДЗ и следующий анализ корней (при решении методом приведения к равносильной смешанной системе уравнений и неравенств необходимость в этом отпадает).
Задания для самостоятельного решения:
Вариант 1.
Решите уравнения
A) 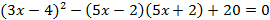
B) 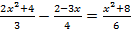
C) 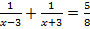
D) 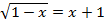
E) 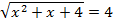
F) 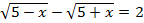
Вариант 2.
Решите уравнения
A) 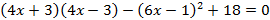
B) 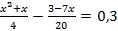
C) 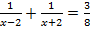
D) 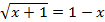
E) 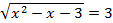
F) 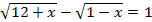
Контрольные вопросы:
1. В какой последовательности решают рациональные уравнения?
2. Какие уравнения называются иррациональными?
3. Какие приемы используют для решения иррациональных уравнений?
Практическая работа
«Решение показательных уравнений различными способами»
Цель работы: Обобщить и систематизировать знания по теме «Показательные уравнения». Закрепить умения использовать полученные знания для решения уравнений
Теоретические сведения к практической работе:
Опред. Показательное уравнение – это уравнение, в котором неизвестное содержится в показателе степени.
Простейшее показательное уравнение имеет вид: aх=b, где а>0 a≠1.
Наличие корней показательного уравнения зависит от числа b. А именно:
1) если b<0 или b=0, уравнение не имеет корней; 2) если b>0, уравнение имеет единственный корень.
Основные способы решения показательных уравнений:
- Уравнивание оснований
- Вынесение общего множителя за скобку
- Введение вспомогательной переменной
Задания для самостоятельного решения:
| 1 вариант | 2 вариант |
| Решите уравнения | |
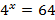
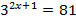
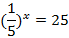
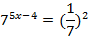
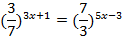
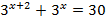
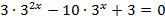
| 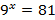
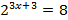
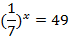
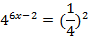
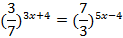
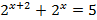
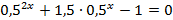
|
Контрольные вопросы:
1. Какие уравнения называются показательными?
2. Каковы особенности решения показательных уравнений?
Практическая работа «Решение тригонометрических уравнений различного типа»
Цель работы: формировать умения решать тригонометрические уравнения различного типа.
Теоретические сведения к практической работе:
Опр. Уравнение называется тригонометрическим, если неизвестная величина входит в него как аргумент тригонометрической функции.

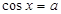 Уравнения вида sin x = a, cos x = a, tg x = a называются простейшими. Для них выведены формулы корней:
Уравнения вида sin x = a, cos x = a, tg x = a называются простейшими. Для них выведены формулы корней:
sin x = a 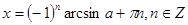
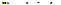
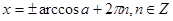
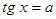
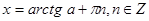

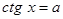
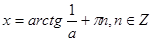
К этим уравнениям сводятся все другие. Для большинства таких уравнений требуется применение различных формул и преобразование тригонометрических выражений.
1. Уравнения, сводящиеся к квадратным 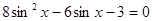 . Вводят новую переменную sin x= t
. Вводят новую переменную sin x= t

2. Уравнения вида 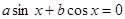 а ≠ 0, b ≠ 0 называются однородными относительно sin x и cos x. Оно решается делением обеих частей на cos x ≠ 0. В результате получается уравнение
а ≠ 0, b ≠ 0 называются однородными относительно sin x и cos x. Оно решается делением обеих частей на cos x ≠ 0. В результате получается уравнение
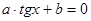 . Этим же способом решается уравнение 2 sin2 x – 5 sin x · cos x + 3 cos 2 x = 0. Обе части уравнения делятся на cos 2 x или sin 2 x
. Этим же способом решается уравнение 2 sin2 x – 5 sin x · cos x + 3 cos 2 x = 0. Обе части уравнения делятся на cos 2 x или sin 2 x

3. Уравнения, решаемые разложением левой части на множители
Пример 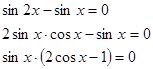
Общий множитель sin x выносится за скобки.
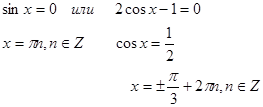
Ответ: 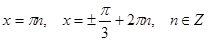
Если уравнение имеет две серии корней, полученных при решении тригонометрических уравнений, имеющую общую часть, в ответе можно оставлять обе серии. Например, х = πn; x = 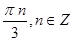
Задания для самостоятельного решения:
Решить уравнения:
1) 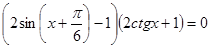 2)
2) 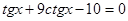
3) 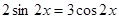 4)
4) 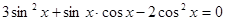
5) 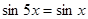 6)
6) 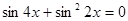
Контрольные вопросы:
1. Какие уравнения являются тригонометрическими?
2. Какие уравнения относятся к простейшим тригонометрическим уравнениям?
3. Какие существуют способы решения более сложных тригонометрических уравнений?