Расчет колонны по условиям первой схемы загружения

Расчет сборной железобетонной колонны.

 

Расчет колонны на сжатие

Полная грузовая площадь для одной внутренней колонны составит

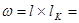7,3×8,3=60,6 м²

Подсчет нагрузок на грузовую площадь сведен в таблицу №2.

Колонну принимаем сечением 400×400 мм. Собственный вес колонны длиной 2,5 м с учетом веса двухсторонней консоли будет (при g_n=0,95);

нормативный - 0,95[0,4×0,4×2,5+(0,3×0,6+0,3×0,3)0,4]25=12,1 кН

расчетный (с g_f=1,1) - 1,1×12,1=13,3 кН

Расчет колонны по прочности на сжатие производим для двух схем загружения:

Расчет колонны по условиям первой схемы загружения

За расчетное принимаем верхнее сечение колонны, расположенное на уровне оси ригеля перекрытия этажа. Расчет выполняется на комбинацию усилий M_max - N, отвечающую загружению временной нагрузкой одного из примыкающих к колонне пролетов ригеля перекрытия этажа и сплошному загружению остальных перекрытий и покрытия.

Табл. №2

Вид нагрузки	Нагрузка (кН/м2)×w×	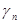Норматив-ная нагрузка (кН)		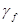Расчет-ная нагрузка
Нагрузка на перекрытие
1.Вес железобетонных конст-рукций перекрытия 2.Вес пола и перегородок 3.Временная нагрузка с коэф. снижения К2=0,8 0,8×5,1=4,1 кН/м2.	3,8×60,6×0,95   2,5×60,6×0,95   4,1×60,6×0,95	218,8   143,9   236,0	1,1   1,1   1,2	240,6   158,3   283,2
Полная нагрузка		598,7		682,1

 

 

а) Определение усилий в колонне. Расчетная продольная сила N.

Постоянная и временная нагрузки на одну колонну от перекрытия собирается с полной грузовой площади w=60,6 м².

Постоянная нагрузка от перекрытия собирается с полной грузовой площади w=60,6 м². Временная нагрузка на перекрытие собирается с половины грузовой площади w/2=30,3 м², учитывается полосовое ее расположение через пролет. Расчетная продольная сила N в расчетном сечении колонны:

N=682,1-283,2/2= 540,5кН.

Расчетный изгибающий момент М.

Для определения момента М в расчетном сечении 1 колонны временную нагрузку на ригеле перекрытия 1-го этажа располагаем в одном из примыкающих к колонне пролетов. Величина расчетной временной нагрузки р на 1 м длины ригеля с учетом коэффициента снижения к₂=0,8.

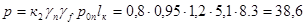кН.

Расчетные высоты колонн будут: для первого этажа

Н₁=Н_1эт+0.15-h_пол-h_пл-h_риг/2=2,5+0,15-0,1-0,55-0,75/2= 1,625 м.

Линейные моменты инерции- колонны сечением 400×400 мм:

для первого этажа 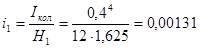м³

-ригеля сечением 300×750 мм, пролетом l=6,0 м:

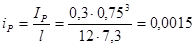м³.

Расчетный изгибающий момент М в расчетном сечении колонны по формуле:

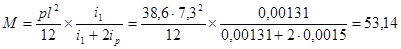кН×м.

б) Расчет колонны по прочности.

По найденным усилиям М=53,14 кН×м и N=540,5 кН колонна рассчитывается на внецентренное сжатие с симметричной арматурой A_s=A_s^/.

Для тяжелого бетона класса В15 имеем расчетное сопротивление бетона R_b=0,9×8,5=7,65 МПа, модуль упругости бетона Е_b=20500 МПа.

Для продольной арматуры класса А-III расчетное сопротивление R_s=R_sc=365 МПа; модуль упругости Е_s=200000 МПа.

Размеры сечения колонны: h=400 мм, b=400 мм, рабочая высота сечения h₀=h-a=400-40=360 мм. Расчетная длина элемента l₀=H₁=1,625 м.

 

Случайный эксцентриситет принимается:

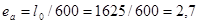мм или 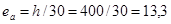мм.

Расчетный эксцентриситет продольной силы:

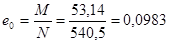м =98,3 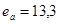мм > мм

В расчет вводится е₀=98,3 мм.

 

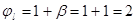
т.к. lo/h=1625/400=4,1 < 10,

е₀/h=98,3/400=0,246 <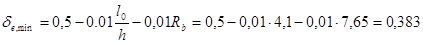

то принимаем 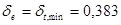. Задаемся коэффициентом армирования 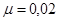(процент армирования m%=2%):

 

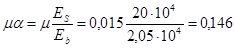
Условная критическая сила равна:

 

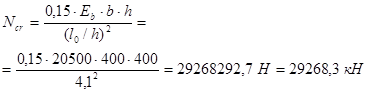
Коэффициент 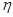определяем по формуле:

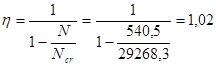
Граничная относительная высота сжатой зоны определяется по формуле:

w=0,85-0,008R_b=0,85-0,008×7,65=0,79

 

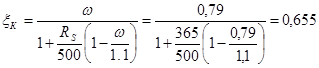
Определяем высоту сжатой зоны

x=N/(R_bb)=540500/(7,65×400)=176,6 мм.

Так как х=176,6 мм < x_Rh_o=0,655×360=236 мм, то площадь продольной арматуры определяем согласно расчетным параметрам по формуле:

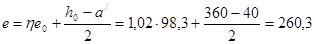мм;

;

;

;

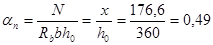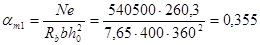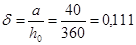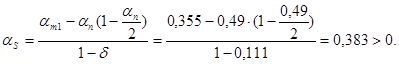
Площадь сечения арматуры:

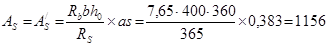мм²

Коэффициент армирования: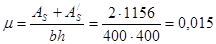

Поскольку полученный коэффициент армирования достаточно близок значению m=0,02, принятому при вычислении N_cr, перерасчет можно не делать.

 

Расчет колонны по усилиям второй схемы загружения.

За расчетное принимается нижнее сечение колонны подвального этажа, расположенное на уровне верха фундамента. Расчет выполняется на комбинацию усилий N_max-M, отвечающих сплошному загружению временной нагрузкой всех междуэтажных перекрытий и покрытия.

а) Определение усилий в колонне. Расчетная продольная сила N.

Постоянная и временная нагрузка на одну внутреннюю колонну от перекрытия собираются с полной грузовой площади w=60,6 м². Учитывается также собственный вес колонны. На основании данных таблицы №2

N=682,1-283,2/2+10=550,5 кН.

Расчетный изгибающий момент М.

Поскольку здание имеет жесткую конструктивную схему и пролеты ригеля, примыкающие к рассматриваемой колонне слева и справа, равны, то при сплошном загружении временной нагрузкой перекрытия изгибающий момент в сечении колонны будет равен нулю, т.е. М=0.

б) Расчет колонны на прочность

В нижнем сечении колонны подвального этажа действует продольная сила N=550,5 кН. Изгибающий момент в сечении М=0. Поскольку расчетный эксцентриситет е₀=М/N=0, сечение рассчитывается на сжатие продольной силой N=550,5 кН, приложенной со случайным эксцентриситетом е_а.

Расчетная длинна колонны l₀=H₁=1,625 м; фактическая длина l=l₀=1,625 м. Отношение l₀/h=1625/400=4,1. Поскольку l₀/h=4,1<20 и случайный коэффициент е_а=h/30=400/30=13,3 мм > l/600=1625/600=2,7 мм

Так как вся временная нагрузка принята длительной то N_l=N=550,5 кН.

При N_l/N=1 и l₀/h=4,1 для тяжелого бетона находим 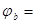0,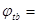920, 0,920

Значение 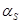вычисляем по формуле:

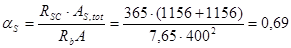
Поскольку 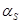=0,69>0,5, принимаем, 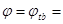0,920.

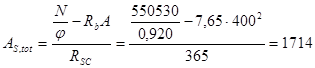мм².

мм²< (As+As¢)=2×1156=2312 мм².

Коэффициент армирования:

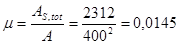
Процент армирования 1,45 % т.е. лежит в пределах оптимального армирования.

Продольную рабочую арматуру подбираем по наибольшей требуемой площади А_s,tot=2312 мм² в количестве 6 Æ25 A-III (фактическая площадь А_s,tot=2945 мм²). Продольные стержни размещаем поровну у граней колонны, перпендикулярных плоскости рамы.

Принимаем у каждой грани 3Æ25A-III с площадью As=As¢= А_s,tot=1473мм².

Принятую продольную арматуру пропускаем по всей длине рассчитываемой монтажной единицы без обрывов. Колонна армируется сварным каркасом из арматуры диаметром 8 мм класса А-I с шагом S=500мм, не превышающим 20d=20×25=500 мм.

 

Расчет консоли колонны

Консоль колонны предназначена для опирания ригеля рамы. Консоли колонны бетонируются одновременно с ее стволом, поэтому выполняется также из тяжелого бетона класса В15; коэффициент условий работы бетона g_b2=0,9. Расчетные сопротивления с учетом g_b2=0,9 равны:

R_b=0,9×8,5=7,65 МПа,

R_bt=0,9×0,75=0,675 МПа,

модуль упругости бетона Е_b=20500 МПа.

Продольная арматура выполняется из стали класса A-III с расчетным сопротивлением R_s=365 МПа. Поперечное армирование коротких консолей выполняется в виде горизонтальных двухветвевых хомутов из стержней диаметром 6 мм класса А-I(площадь сечения одной ветви хомута A_sw1=28,3).

Модуль упругости поперечных стержней Е_s=210000(МПа). Консоль воспринимает нагрузку от одного междуэтажного перекрытия с грузовой площади w/2=30,3 м². Согласно данным табл.№2, расчетная поперечная сила передаваемая на консоль, составляет:

Q=682,1/2=341,1 кН.

Принимаем вылет консоли l_c=300 мм, высоту сечения консоли в месте примыкания ее к колонне, h=600 мм. Угол наклона сжатой грани консоли к горизонту 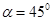. Высота сечения у свободного края

h₁=600-300=300 мм > h/3=200 мм. Рабочая высота опорного сечения консоли

h₀=h-a=600-30=570 мм. Поскольку l_c=300<0,9h=513 мм, консоль - короткая.

С учетом зазора между торцом ригеля и гранью колонны 60 мм длина площадки опирания ригеля вдоль вылета консоли будет

Расстояние от приложения силы Q до опорного сечения консоли будет:

a=l_c-l_sup/2=300-240/2=180 мм.

Проверяем прочность бетона на смятие под опорной площадкой:

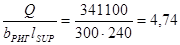Мпа < R_b=7,65 МПа, т.е. прочность на смятие обеспечена.

Проверяем условие прочности по наклонной сжатой полосе:

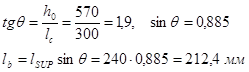
Принимаем шаг горизонтальных хомутов S_w=150 мм (S_w<h/4≤150 мм);

A_sw=n∙A_sw1=2×28,3=57 мм²,

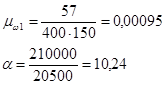
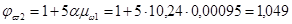
Проверяем условие прочности:

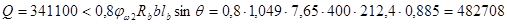Н<3,5∙R_bt∙b∙h_o=

=3,5∙0,675∙400∙570=538650 Н.

Условие прочности выполняется, поэтому высота консоли достаточна для восприятия поперечной силы.

Определяем площадь продольной арматуры А_s. Момент в опорном сечении, взятый с коэффициентом 1,25 равен:

М=1,25Q_a=1,25×341,1 ×0,18=76,8 кН∙м.

Площадь сечения арматуры будет равна:

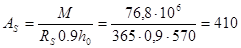мм²

Принимаем 2 Æ 18 A-III с площадью А_s=509 мм².

 

Литература.

1. СНиП 2.03.01-84*. Бетонные и железобетонные конструкции.

2. СНиП 2.01.07-85*. Нагрузки и воздействия.

3. Байков В. Сигалов Э. Е. Железобетонные конструкции. Общий курс. Издание пятое. - М.: Стройиздат, 1991