Для определения положения какого-либо события в пространстве требуется произвести три измерения и указать три числа, называемые пространственными координатами, т.е. физическое пространство, в отличие от времени, трехмерно.
Пространственные координаты одного и того же события относительны: они зависят от выбора начала отсчета пространственных координат и поэтому сами по себе не могут служить объективными характеристиками пространственных отношений. Расстояние между двумя точками на оси, которые показывают положение 2 различных материальных объектов настолько мало, что не зависит от выбора точки отсчета, поэтому его можно выбирать в качестве объективной характеристики пространственных отношений. Это свойство пространства – его однородность.
Полная шкала расстояний, освоенная физикой, охватывает более сорока порядков.
Важнейшее свойство пространства – его изотропность, которое означает физическое равноправие всех направлений в пространстве. То есть, всякая изолированная система обладает фундаментальной характеристикой, называемой полным моментом, которая сохраняется со временем.
Для объективного описания физических величин можно использовать только векторы и скаляры, ибо в этом случае, как сами величины, так и форма соотношений между ними, остаются одинаковыми во всех системах координат, отличающихся выбором начала отсчета и направлений осей. Примером скалярных величин служат такие характеристики, как масса, энергия, температура. Примерами векторных величин являются скорость, импульс, момент вращения, сила. Их принято изображать направленными отрезками (стрелками) в определенном масштабе.
Процесс измерения расстояния сопряжен с процессом измерения времени, причем в разных точках пространства. И наоборот.
Взаимосвязанное описание пространственно-временных отношений можно ввести, рассматривая движение материального объекта более строго. Тело отсчета, относительно которого измеряются все расстояния вдоль выбранной оси, вместе с совокупностью «местных» часов, расположенных в каждой точке этой оси, называется системой отсчета (СО). Пока мы условно будем считать ее неподвижной.
В заданной СО каждому событию, характеризующему, где и когда находится материальный объект, соответствуют два числа х и t, называемые пространственно-временными координатами события. То есть в самом простейшем случае природные явления можно описать в двумерном мире событий.
Если два события происходят в одной точке пространства (т.е. одноместно), то промежуток времени между ними может измеряться по одним и тем же часам, расположенным там же. Если же мы измеряем расстояние между двумя удаленными событиями, то это следует делать жесткой линейкой в один и тот же момент времени (одновременно).
Представление о едином пространстве-времени, или мире событий, обязательно требует синхронизации «местных» часов. Если это достигнуто, то отсчет времени может производиться по единым часам, установленным в начале отсчета системы координат, что и означает введение единого времени.
Учитывая трехмерность реального пространства, мир событий в общем случае представляет собой единое четырехмерное пространство-время, называемое миром событий. Движение частицы в мире событий считается заданным, если нам удалось узнать зависимость ее положения в пространстве от времени, т.е. закон движения r = r (t).
Галилей первым понял, что описание движений любых тел выглядит одинаково как в неподвижной системе отсчета, так и в любой системе отсчета, которая движется равномерно и прямолинейно с постоянной скоростью относительно условно неподвижной СО. Такие СО называются инерциальными (ИСО). Соответственно, СО, движущиеся ускоренно, называются неинерциальными (НСО).
Результаты исследований Галилея и затем Ньютона привели к открытию первого фундаментального закона природы – принципа инерции. Он гласит: существуют такие СО, в которых любая свободная частица движется равномерно и прямолинейно. Таким образом, ИСО от неинерциальной СО можно отличить по тому, как ведет себя в ней свободная частица. Состояния равномерного прямолинейного движения и покоя является относительными.
Если ограничиться только скоростями, малыми по сравнению со скоростью света, то пространственные и временные отношения во всех инерциальных системах отсчета описываются одинаково. В ИСО расстояния и промежутки времени остаются неизменными относительно выбора таких систем отсчета. Что касается скорости частицы относительно разных ИСО, то она, естественно, имеет в них различные значения. В справедливости этого утверждения при малых скоростях мы можем убедиться, сравнивая скорость перемещения пассажира внутри вагона с его скоростью относительно поверхности Земли.
4. Законы сохранения импульса (количество движения) и полной механической энергии системы
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю[1].
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении системы в пустом пространстве импульс сохраняется во времени, а при наличии внешнего воздействия скорость изменения импульса определяется суммой приложенных сил.
Как и любой из фундаментальных законов сохранения, закон сохранения импульса связан, согласно теореме Нётер, с одной из фундаментальных симметрий, — однородностью пространства [2].
Закон сохранения импульса впервые был сформулирован Р. Декартом[3]
Полная механическая энергия – сумма кинетической и потенциальной энергии всех тел, входящих в систему:
.
По теореме о кинетической энергии работа всех сил, действующих на все тела 
. Если в системе все силы потенциальные, то справедливо утверждение: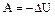 
. Следовательно:
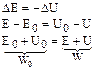
Полная механическая энергия замкнутой системы есть величина постоянная (если в системе действуют только потенциальные силы).
Если в системе есть силы трения, то можно применить следующий прием: силу трения назначаем внешней силой и применяем закон изменения полной механической энергии:
.
Работа внешней силы равна изменению полной механической энергии системы.
7) Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними.
8) Мощностью называют отношение работы А к интервалу времени ∆t, за который эта работа совершена.
9) Если тело или система тел могут совершать работу, то говорят, что они обладают энергией.
10) Кинетическая энергия – равна работе, которую надо совершить, чтобы увеличить скорость тела от нуля до значения U.
11) Потенциальная энергия – величина, равная произведению массы тела на ускорение свободного падения g и высоту h тела над поверхностью земли.
12) ЗСЭ: В замкнутой системе, в которой действуют консервативные силы, механическая энергия сохраняется. E = Ek+Ep = const.
5. Основное уравнение динамики вращательного движения. Закон сохранения момента импульса движения.
Уравнение (3) M = d L / dt называется основным уравнением динамики вращательного движения: скорость изменения момента импульса тела, вращающегося вокруг неподвижной точки, равна результирующему моменту относительно этой точки всех внешних сил, приложенных к телу.
Из уравнений (1) и (3) следует М = d ( I ω) / dt = I d ω / dt = I e,
или e = М / I.
Угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.