ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 18

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 18

По дисциплине: ЭЛЕМЕНТЫВЫСШЕЙ МАТЕМАТИКИ

Наименование работы: ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ.

 

 

Для специальности 230111, 230115.

 

Составлено преподавателем Калмыковой О.И.

 

 

г. Смоленск

2012 г.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 18

По дисциплине: ЭЛЕМЕНТЫВЫСШЕЙ МАТЕМАТИКИ (2 курс)

Наименование работы: ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ.

 

1. Цель работы: Приобрести навыки выполнения действий над комплексными числами в алгебраической форме (сложение, вычитание, умножение, деление).

2. Литература:

2.1. Богомолов Н.В. Практические занятия по математике: М.; Высшая школа, 1990.

3. Подготовка к работе:

3.1. Изучить теоретический материал по теме “Комплексные числа и их геометрическая интерпретация. Действия над комплексными числами в алгебраической форме”.

3.2. Действия над комплексными числами в алгебраической форме (сложение, вычитание, умножение, деление).

3.3. Подготовить бланки отчета.

3.4. Подготовить ответы на вопросы допуска к работе.

3.4.1. Понятие равенства двух комплексных чисел.

3.4.2. Понятии двух сопряженных комплексных чисел.

3.4.3. Основное свойство мнимой единицы.

3.4.4. Правила выполнения действий над комплексными числами.

4. Основное оборудование:

4.1. Литература, конспект.

5. Задание:

5.1. Выполнить действия в алгебраической форме.

5.2. Найти корни квадратного уравнения.

6. Порядок выполнения работы:

6.1. Записать задание своего варианта в отчет.

6.2. Выполнить четыре действия с каждой парой комплексных чисел.

6.3. Выполнить дополнительное задание.

6.4. Записать ответы, оформить отчет

6.5. Подготовить ответы на контрольные вопросы.

7. Содержание отчета:

7.1. Титульный лист.

7.2. Цель работы.

7.3. Результаты и ход выполнения работы.

7.4. Выводы отчеты.

8. Контрольные вопросы:

8.1. Основное свойство мнимой единицы.

8.2. Понятие комплексного числа.

8.3. Геометрическая интерпретация комплексного числа, множество комплексных чисел К.

8.4. Правила действия над комплексными числами в алгебраической форме (сложение, вычитание, умножение, деление).

9. Приложение:

Вариант 1. Вариант 2. Вариант 3.

1) 1) 1)

2) x²-4x+16=0 2) x²-2x+4=0 2) x²-28x+27=0

 

Вариант 4. Вариант 5. Вариант 6.

1) 1) 1)

2) (2x+3)²-9(2x+3)+8=0 2) x⁴+x²+1=0 2) x²-2x+5=0

10. Методические указания:

Комплексными числами называются числа вида a+bi, где a и b – действительные числа, а число i, определяемое равенством i²=-1, называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:

1) два комплексных числа a₁+b₁i и a₂+b₂i называются равными, если a₁=a₂ и b₁=b₂;

2) суммой двух комплексных чисел a₁+b₁i и a₂+b₂i называется комплексное число (a₁+a₂)+(b₁+b₁)i;

3) произведением двух комплексных чисел a₁+b₁i и a₂+b₂i называется комплексное число (a₁a₂-b₁b₂)+(a₁b₂-a₂b₁)i.

Запись комплексного числа в виде z=a+bi называется алгебраической формой записи комплексного числа.

Действительное число a называется действительной частью комплексного числа z=a+bi, а действительное число b – мнимой частью.

Любое действительное число a содержит в множестве комплексных чисел, его можно записать так: . Числа 0, 1 и i записываются соответственно в виде , и .

При a=0 комплексное число a+bi обращается в число мнимое число bi.

Комплексное число вида a-bi называется комплексно сопряженным с числом a+bi и обозначается , т. е. .

Комплексные числа вида a+bi и – a-bi называются противоположными.

 

Пример 1.

(4+2i)+(1+5i)

По правилу сложения комплексных чисел получим:

(4+2i)+(1+5i)=(4+1)+(2+5)i=5+7i.

 

Пример 2.

(3+5i)-(6+3i)

По правилу сложения комплексных чисел получим:

(3+5i)-(6+3i)=(3-6)+(5-3)i=-3+2i.

Сложение (вычитание) комплексных чисел сводится к сложению (вычитанию) векторов, изображающих эти числа. Действия над заданными векторами показаны на рисунке.

 

Комплексное число z=a+bi можно изображать точкой плоскости с координатами (a;b) (рис.)

При этом действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а число мнимых чисел – точками оси ординат, которую называют мнимой осью.

Каждой точке плоскости с координатами (a;b) соответствует один и только один вектор с началом в точке О (0;0) и концом в точке M(a;b). Поэтому комплексное число a+bi можно изобразить в виде вектора 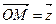с началом в точке z=0 и концом в точке z=a+bi.

Из геометрической интерпретации комплексного числа вытекают следующие свойства:

1. Длина вектора равна .
2. Точки z=a+bi и z=a-bi симметричны относительно действительной оси.
3. Точки z и – z симметричны относительно точки z=0.
4. Число z₁+z₂ геометрически изображается как вектор, построенный по правилу сложения векторов, соответствующих точкам z₁ и z₂ (рис.)

 

1. Расстояние между точками z₁ и z₂ равно (рис.)

 

 

Пример 3.

Вычислить: i¹⁶

Решение: i¹⁶=i^4*4=1

 

 

Пример 4.

Выполнить действия: (2-3i)(2+3i)

Решение: (2-3i)(2+3i)=4-9i²=4+9=13

Пример 5.

Выполнить действия:

Решение: умножаем делимое и делитель на множитель, сопряженный делителю: