Раздел 2 Основы дискретной математики

· Элементы и множества. Способы задания множеств

Множество - совокупность объектов, объединенных по определенному признаку.

Множество состоит из элементов. Множества обозначают заглавными буквами латинского алфавита A, В, С.... Элементы множества обозначают малыми латинскими буквами а, b, с,

Принадлежность элемента а к множеству N записывают: а N
Перечисление всех объектов, входящих в множество: N ={а, в,с}.

Описание характеристических свойств, которыми обла­дают все элементы множества.

Обозначается: N = {х| Р(х)} или N = {х: Р(х)}.

Множество А называют подмножеством множества В, если каждый элемент множества A является элементом множества В. Обозначается А В.

Среди всех множеств выделяется пустое множество, которое не содержит ни одного элемента. Пустое множество обозначается знаком .

Если одновременно А В и В А, то говорят, что множества А и В равны (А = В).

· Операции над множествами. Диаграммы Эйлера-Венна. Свойства операций над множествами
Для наглядного представления операций над множествами применяют своего рода диаграммы. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его - кругов Эйлера, представляющих множества. Вместо кругов Эйлера определенные множества изображают любые другие замкнутые фигуры, и такую иллюстрацию называют диаграммами Венна. Для рассуждений, связанных с множествами, используют язык диаграмм Эйлера-Венна.

Объединение множеств А₁ и А₂ называют множество В, состоящее их всех тех элементов,

которые принадлежат хотя бы одному их множеств А₁, А₂ (рис. 12а),обозначается: B = A₁ A₂, или В= {х|х A_lили х А₂}.

Пересечение множеств А₁ и А₂ называется множество B,состоящее из тех и только тех

элементов, которые принадлежат и множеству и множеству А₂ одновременно (рис. 12б), обозначается: В = А₁ А₂ или В = {х| х А_х и х А_г }.

Разность множеств А₁ и A₂ называют множество B, состоящее только из тех элементов

множества А₁, которые не содержатся в A₂(рис. 12в), обозначается: В=А₁\А₂, или В= {х\х? А_ъ х<£А₂}. Пусть U - универсальное множество такое, что все рассматриваемые множества являются его подмножествами.

Дополнение (до U) множества A называется множество всех элементов, не

принадлежащих А, но принадлежащих универсальному множеству U(рис. 12г), обозначается:

=U\A.

Рисунок 12

· Отношения. Свойства отношений
Функция

Рассмотрим некоторое отображение f:Х Y. Это отображение называют функцией, если оно одно­значно, т. е. если для любых пар (х₁y₁) f и (х₂y₂) f из x₂= x₁ следует y₂= y₁.

На рис. 1.5, а приведен пример отображения, явля­ющегося функцией. Отображение на рис. 1.5, б функцией не является.

Из определения отображения и из приведенных ранее примеров следует, что элементами множеств Х и Y мо­гут быть объекты любой природы. Однако в задачах компьютерных сетей большой интерес представляют отображения, которые являются однозначными и множество значений которых представляет собой множество вещественных чи­сел R. Однозначное отображение f, определенное выше, называют функцией с вещественными значениями, если .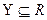

а) б)

Рис. 1.5. Иллюстрация к понятию функции

Понятие функции является чрезвычайно широким, и изучению отдельных классов функций посвящены многие математические дисциплины (алгебра, тригонометрия и т.п.). Мы рассмотрим только некоторые общие наибо­лее фундаментальные свойства функции, не касаясь свойств конкретных классов.

Значение у в любой из пар (х, y) f называют функ­цией от данного х и записывают в виде y=f(x). Такая запись позволяет вести следующее формальное определе­ние функции:

f= {(x, y) =f (x)}. (1.19)

Таким образом, символ f используют при определении Функции в двух смыслах:

f является множеством, элементами которого будут пары (х, y), участвующие в соответствии;

f (x) является обозначением для у У, соответствую­щего данному х Х.

Как уже указывалось, термин «отношение» использу­ют для обозначения некоторых видов отображений, за­данных на одном и том же множестве. В связи с этим удобно вести специальную символику.

Пусть отображение (X, Г) является отношением. Рас­смотрим элемент у Г х. Будем говорить, что элемент у находится в отношении Г к элементу х, и запишем это в виде у Г х. (1.20)

Используя для отображения, заданного на одном множестве, соотношение (X, Г), получаем, что отношение есть пара множеств (X, Г), в которой Г 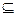Х². Поскольку элементами множества X² являются упорядоченные пары, то можно сказать, что отношение есть множество упорядоченных пар. Так как каждая пара связывает между собой только два элемента множества X², то такое отношение называют бинарным.

Можно ввести более общее понятие отношения, называя отноше­нием пару множества (X, Г), где Г 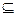Х ⁿ. Элементами множества Х ⁿ являются упорядоченные n-ки, что позволяет назвать данное отноше­ние n-арным. В частности, множество упорядоченных троек может быть названо тернарным отношением. В дальнейшем, не оговаривая этого особо под термином «отношение» будем иметь в виду бинарное отно­шение.

Отношения делятся на различные виды в зависимости от того, обладают или не обладают они некоторыми свой­ствами. Рассмотрим шесть основных свойств отношений. При описании этих свойств будем считать, что х, у и z — любые элементы из множества X.

Рефлективность: х Г х истинно; антирефлексивность: х Г х ложно; симметричность: х Г у у Г х; антисимметрич­ность: х Г у и у Г х х=у; несимметричность: если х Г у ис­тинно, то у Г х ложно; транзитивность: х Г у и y Г z x Г z.

Воспользовавшись описанными свойствами, рассмотрим некоторые важные виды отношений.

· Графы. Основные определения. Элементы графов
Графические представления - удобный способ иллюстрации различных понятий, отображения исследуемого процесса. Мощными и наиболее исследованным классом объектов, относящихся к графическим представлениям, являются так называемые графы.

Граф - конечная совокупность точек, называемых вершинами; некоторые из них соединены друг с другом линиями, называемыми ребрами графа. Рёбра графа могут изображаться как прямыми, так и кривыми линиями.

· Виды графов. Операции над графами
Если вершина графа не соединена с другими вершинами отрезками, её можно назвать изолированной. Если каждая вершина графа соединена отрезками со всеми остальными, то граф будет называться полным.

Граф называется ориентированным, если указано направление дуг, неориентированным, если такое направление не указано. Граф называется петлей, если его начало и конец совпадают.

Две вершины называются смежными, если существует соединяющая их дуга.

Степенью (валентностью) вершины называется число ребер графа, которым принадлежит эта вершина. Кратностью пары вершин называется число соединяющих их ребер

или дуг. Подграфом G_a графа G называется граф, в который входит лишь часть вершин графа G вместе с дугами их соединяющими. Частным графом G_b графа называется граф, в который входит лишь часть дуг графа G вместе с вершинами их соединяющими.

Путем в графе G называется такая последовательность дуг, в которой конец каждой последующей дуги совпадает с началом предыдущей. Длиной пути называют число входящих в этот путь дуг. Путь может быть конечным и бесконечным. Путь, в котором никакая дуга не встречается дважды, называется элементарным путём. Контур – это конечный путь, у которого начальная и конечная вершины совпадают. Контур называется элементарным, если все его вершины различны (кроме начальной и конечной). Контур единичной дуги называется петлей.

В неориентированном графе понятие дуга, путь, контур заменяются соответственно на ребро, цепь, цикл. Ребро – отрезок, соединяющий две вершины, цеп ь – последовательность ребер. Цикл – конечная цепь, у которой начальная и конечная вершина совпадают.

Граф называется связанным, если любые его две вершины можно соединить цепью. Граф, который не является связанным, может быть разбит на конечное число связных графов, называемых компонентами, или частями. Ребро графа G называется мостом, если граф, полученный из G путем удаления этого ребра, имеет больше компонент связности, чем граф G.

Точкой сочленения графа называется вершина, удаление которой приводит к увеличению числа его компонент связности.

Гамильтонов путь на графе – путь, проходящий по одному разу через все вершины графа.