· Численное интегрирование. Формулы прямоугольников, трапеций, Симпсона
Не все, даже сравнительно простые функции, могут быть проинтегрированы с помощью
элементарных функций. С другой стороны, определенный интеграл от непрерывной функции y= ƒ(x) обязательно существует. Поэтому важное значение имеют методы приближенного вычисления определенного интеграла, основанные на том, чтоопределенный интеграл  , где a<bвычисляется как площадь криволинейнойтрапеции.
, где a<bвычисляется как площадь криволинейнойтрапеции.
Формула прямоугольников
Площадь криволинейной трапеции заменяется суммарной площадью прямоугольников, интервал  разбивается на n равных частей длины h=
разбивается на n равных частей длины h=  и для точек деления x0, x1,x2…xn вычисляются значения интегрируемой функции y=ƒ(x), считая, что x0 = a и xn = b. Интегралсчитается по формуле:
и для точек деления x0, x1,x2…xn вычисляются значения интегрируемой функции y=ƒ(x), считая, что x0 = a и xn = b. Интегралсчитается по формуле:  Вычисленное значение тем точнее, чем больше n. Оценка погрешности при вычислении по формуле прямоугольников определяется выражением: R
Вычисленное значение тем точнее, чем больше n. Оценка погрешности при вычислении по формуле прямоугольников определяется выражением: R 
 где
где  - максимальная величина абсолютного значения первойпроизводной во всем интервале интегрирования, причем
- максимальная величина абсолютного значения первойпроизводной во всем интервале интегрирования, причем 
Формула трапеций
В данном методе приближенного вычисления определенного интеграла площадь
криволинейной трапеции заменяется площадью прямолинейной трапеции. Интеграл находят по формуле:  Абсолютное значение остаточного члена не превышает значения
Абсолютное значение остаточного члена не превышает значения  Формула Симпсона
Формула Симпсона
Значительно более точные результаты получаются, если площадь криволинейной трапеции заменяют площадью полосы, ограниченной сверху не прямой линией, а дугой параболы, проходящей через три точки кривой с абсциссами a, x1= a+h и b=a+2h
Определённый интеграл равен 
Абсолютное значение остаточного члена:  .
.
• Абсолютная погрешность при численном интегрировании.
Численное дифференцирование. Интерполяционные формулы Ньютона.
В ряде случаев возникает необходимость найти производные от функции  , заданной таблично. Возможно также, что непосредственное дифференцирование функции оказывается слишком сложным в силу особенностей аналитического задания функции. В этих случаях прибегают к приближенному дифференцированию. Для вывода формулы приближенного дифференцирования данную функцию
, заданной таблично. Возможно также, что непосредственное дифференцирование функции оказывается слишком сложным в силу особенностей аналитического задания функции. В этих случаях прибегают к приближенному дифференцированию. Для вывода формулы приближенного дифференцирования данную функцию  заменяют интерполяционным полиномом
заменяют интерполяционным полиномом  , и полагают:
, и полагают:  на отрезке
на отрезке 
Интерполяционный полином Ньютона:

где  - шаг интерполяции
- шаг интерполяции
 - первая конечная разность:
- первая конечная разность:  .
.
 - вторая конечная разность:
- вторая конечная разность:  .
.
 - конечные разности высших порядков:
- конечные разности высших порядков:  .
.
Производя перемножение и раскрывая факториал, получаем:

Учитывая, что  , получаем формулу приближенногодифференцирования:
, получаем формулу приближенногодифференцирования:

Аналогично для второй производной:


Таким же способом можно вычислить производную любого порядка.
Если функция задана таблично, и значение производной нужно вычислить в узловых точках  , то каждое табличное значение принимают за начальное
, то каждое табличное значение принимают за начальное  и тогда
и тогда  и формулы численного дифференцирования существенно упрощаются:
и формулы численного дифференцирования существенно упрощаются:  .
.
Для второй производной:
 .
.
Погрешности для вычисления производной определяются по формуле: 
где  - это максимальный порядок конечной разности, входящий в интерполяционный полиномНьютона
- это максимальный порядок конечной разности, входящий в интерполяционный полиномНьютона  .В формулы численного дифференцирования входят конечные разности разных порядков функции
.В формулы численного дифференцирования входят конечные разности разных порядков функции  . Справедливо общее утверждение: если полином
. Справедливо общее утверждение: если полином  является полиномом n-ой степени, то конечная разность -го порядка – постоянная величина:
является полиномом n-ой степени, то конечная разность -го порядка – постоянная величина:  Конечные разности порядка выше, чем n, равны нулю.В случае табличного задания функции
Конечные разности порядка выше, чем n, равны нулю.В случае табличного задания функции  для системы равноотстоящих точек
для системы равноотстоящих точек  где
где  конечные разности определяются по формулам:
конечные разности определяются по формулам:

 …………….
…………….
 )
)
Вычисленные конечные разности различных порядков располагают в форме таблицы, которую называют горизонтальной таблицей разностей или просто таблицей конечных разностей.

| 
| 
| 
| 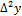
| 
| 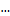
|

| 
| 
| 
| 
| 
| 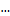
|

| 
| 
| 
| 
| 
| 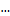
|

| 
| 
| 
| 
| 
| 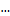
|
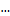
| 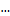
| 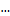
| 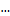
| 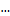
| 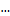
| 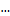
|
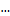
| 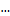
| 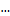
| 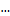
| 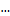
| 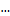
| 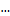
|
· Погрешность в определении производной. Таблица конечных разностей
Различают априорную и апостериорную оценки погрешности.
Априорная оценка погрешности - та, которая может быть получена до решения задачи. Она позволяет сначала определить, при каких параметрах математической модели может быть получена удовлетворительная точность и только после этого провести решение поставленной задачи. Такая последовательность действий является наиболее рациональной. Однако на практике получить априорную оценку погрешности удается нечасто.
Апостериорная оценка погрешности - та, которая получается после (в результате) решения задачи. Для этого, как правило, необходимо получить несколько решений задачи с различными параметрами математической модели. Такой подход более трудоемок, но обычно он бывает единственно возможным.
Таблица конечных разностей
Приходится рассматривать функция заданную таблично  где
где

Конечные разности последовательности yiопределяется соотношением

Вспомним бином Ньютона, можно показать что n-я конечная разностьyiможет быть представлена как сумма 
Данные конечные разности удобно располагать виде таблиц:
Горизонтальная
Диагональная
Чаще на практике используется горизонтальная таблица она имеет вид:
| x | y | y | 2y | 3y |
| x0 | y0 | y0 | 2 y0 | 3 y0 |
| x1 | y1 | y1 | 2y1 | 3y1 |
| x2 | y2 | y2 | 2 y2 | 3 y2 |
| … | … | .. | … | … |
| xn | yn | yn | 2 yn | 3 yn |
Диагональная
| x | y | y | 2y | 3y |
| x0 | y0 | y0 | ||
| x1 | y1 | 2 y0 | ||
| x2 | y1 | 2y1 | 3 y0 |
· Численные методы решения дифференциальных уравнений. Метод Эйлера для решения задачи Коши. Построение интегральной кривой
Обыкновенное дифференциальное уравнение имеет бесчисленное множество решений.
Однако, задание начальных условий позволяет получить вполне определенное решение
дифференциального уравнения. Нахождение частного решения дифференциального уравнения
 порядка, удовлетворяющего заданным начальным условиям называют задачей Коши.
порядка, удовлетворяющего заданным начальным условиям называют задачей Коши.
Теорема Коши (теорема существования и единственности решения дифференциального уравнения при заданном начальном условии): если функция  непрерывна в некоторой области около точки
непрерывна в некоторой области около точки  т.е. при
т.е. при  и
и  то существует по крайней мере одно решение уравнения
то существует по крайней мере одно решение уравнения  принимающее при
принимающее при  значение
значение  , определенное непрерывное в некотором интервале около
, определенное непрерывное в некотором интервале около  . Если кроме того
. Если кроме того  имеет в рассматриваемой области ограниченную частную производную
имеет в рассматриваемой области ограниченную частную производную  , то существует единственное решение
, то существует единственное решение  обыкновенного дифференциального уравнения первого порядка.
обыкновенного дифференциального уравнения первого порядка.