Алгоритм определения ускорений звеньев механизма
1. Провести структурный анализ механизма (мы уже сделали).
2. Начертить кинематическую схему механизма в нескольких положениях, то есть решить первую задачу кинематического анализа механизма (мы уже сделали).
3. Определить скорости для начального механизма и всех групп Ассура. Определить численное значение угловой скорости
2-го звена (шатуна) (мы уже сделали).
4. Определить ускорения для ведущего звена начального механизма.
5. Определить ускорения для каждой группы Ассура, в порядке их присоединения к начальному механизму.
Краткие пояснения к рисункам. Вектор ускорения точки В (ɑB) равен сумме двух векторов: вектор ускорения точки А (ɑA) плюс вектор относительного ускорения точки В относительно точки А (ɑBA):
ɑB = ɑA + ɑBA
Но так как ускорение точки А равно нулю, то вектор ускорения точки В (ɑB) равен вектору относительного ускорения (ɑBA).
ɑB = ɑBA
Вектор относительного ускорения ɑBA раскладываем на две составляющие: ɑnBA (нормальная составляющая ускорения) и ɑτBA (тангенциальная составляющая ускорения).
ɑBA = ɑnBA + ɑτBA,
тогда:
ɑB = ɑnBA + ɑτBA.
Вектор ɑnBA всегда направлен параллельно звену АВ от точки В к точке А. Численное значение вектора ɑnBA определяют по формуле:
ɑnBA = ω21 х LАВ.
Вектор ɑτBA всегда направлен перпендикулярно звену АВ в сторону углового ускорения звена Ԑ1. Численное значение вектора ɑτBA определяют по формуле:
ɑτBA = Ԑ1 х LАВ .
При кинематическом анализе механизма обычно считают, что угловая скорость кривошипа постоянна: ω1 = const.
В этом случае угловое ускорение равно нулю: Ԑ1 = 0, а следовательно численное значение ɑτBA = 0.
В итоге получаем векторное ускорения для кривошипа начального механизма:
ɑB = ɑnBA
План ускорений для звена АВ строим с использованием масштабного коэффициента плана ускорений. Допустим, что получили численное значение ɑBA = 840 м/с2. Тогда масштабный коэффициент плана ускорений определяется так:
μɑ = 840 м/с2: 42 мм = 20 м/с2/мм.
Построение плана ускорений начинаем с точки Π – полюса плана ускорений. В полюсе ускорения всех точек равны нулю, следовательно в полюс попадает точка А, так как ее ускорение равно нулю. На плане ускорений, ускорения точек звена обозначаются прописными буквами (а,в,с). Из полюса проводим отрезок со стрелкой длиной 42 мм параллельно звену АВ от точки В к точке А. Этот отрезок будет изображать в масштабном коэффициенте вектор ускорения точки В.

Вычерчиваем группу Ассура, состоящую из двух звеньев: 2 – шатун, 3 – ползун. В группе Ассура вектор ускорения точки В уже известен и по величине и по направлению.
Неизвестными являются векторы ускорений двух точек: точки С, лежащей на шатуне и точки С, лежащей на ползуне.
У вектора ускорения точки С (ɑC), лежащей на ползуне, неизвестны: ни величина, ни направление. Единственное, что мы знаем про вектор ускорения точки С: он направлен параллельно направляющей ХХ ползуна (вверх или вниз – неизвестно).
Вектор ускорения точки С (ɑC), лежащей на шатуне, равен сумме двух векторов: вектор ускорения точки В (ɑВ) плюс вектор относительного ускорения точки С относительно точки В (ɑСB).
Вектор относительного ускорения ɑСВ раскладываем на две составляющие: ɑnСВ (нормальная составляющая ускорения) и ɑτСВ (тангенциальная составляющая ускорения).
ɑСВ = ɑnСВ + ɑτСВ,
тогда:
ɑС = ɑnСВ + ɑτСВ.
Вектор ɑnСВ всегда направлен параллельно звену СВ от точки С к точке В. Численное значение вектора ɑnСВ определяют по формуле:
ɑnСВ = ω22 х LВС.
Допустим, что численное значение ɑnСВ = 200 м/с2. Тогда длина этого вектора на плане ускорений в масштабном коэффициенте плана ускорений будет равна:
200 м/с2 : μɑ = 200 м/с2 : 20 м/с2/мм = 10 мм.
Внимание! ω2 – мы определили при построении плана скоростей.
Вектор ɑτСВ всегда направлен перпендикулярно звену СВ в сторону углового ускорения звена Ԑ2. Так как мы не знаем ни численного значения ни направления Ԑ2, то следовательно мы не знаем численного значения ɑτСВ. Также мы не знаем как направлен вектор ɑτСВ : по часовой стрелке или против. Единственное что мы знаем о векторе ɑτСВ: он направлен перпендикулярно звену СВ.
Таким образом, мы получаем векторное уравнение с двумя неизвестными:
ɑС = ɑВ + ɑnСВ + ɑτСВ
??
Данное векторное уравнение решаем следующим образом: на плане ускорений к вектору ɑВ прибавляем вектор ɑnСВ, то есть через точку в на плане ускорений откладываем отрезок длиной 10 мм параллельно звену СВ от точки С к точке В. Два векторасложили.

Теперь прибавляем третий вектор - ɑτСВ . Этот вектор проводим через конец вектора ɑnСВ (вправо и влево)перпендикулярно звену СВ.

Результирующий вектор ɑС должен идти из начала сложения векторов (из полюса Π) (вверх и вниз) параллельно направляющей ХХ, до пересечения с вектором ɑτСВ.
Точку пересечения этих двух векторов обозначает точкой с.
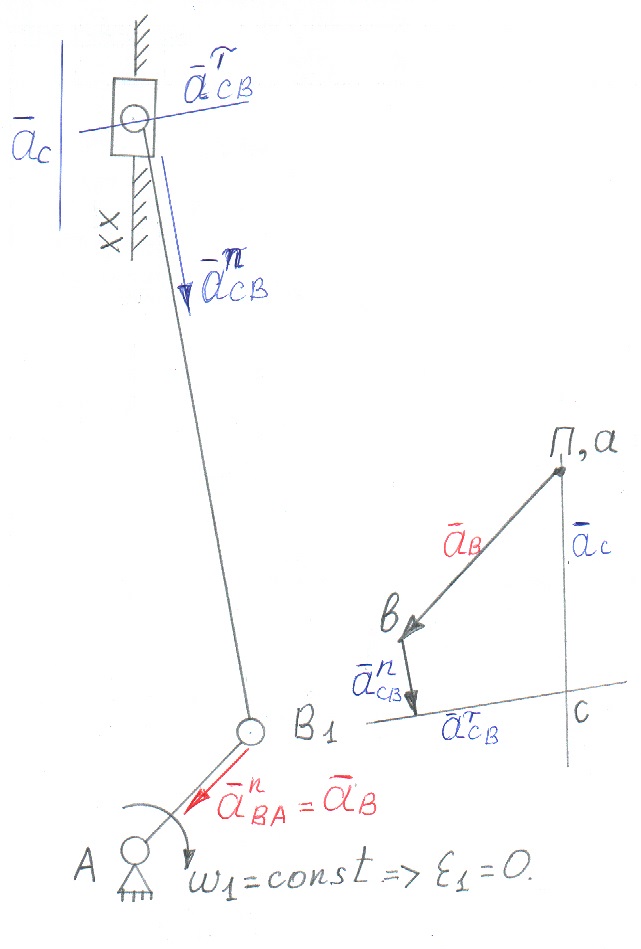
На плане ускорений расставляем стрелки (направления векторов) по правилу: раз к вектору ɑВ ивектору ɑnСВ прибавиливектор ɑτСВ , то они должны следовать друг за другом, а результирующий вектор ɑС должен быть направлен из полюса Π к точке С на плане ускорений.
Таким образом, тангенциальная составляющая ускорения ɑτСВ направлена по часовой стрелке, а следовательно,
Ԑ2 - угловое ускорение второго звана – шатуна, также будет направлена по часовой стрелке.
Численное значение Ԑ2 определяем по формуле: Ԑ2 = ɑτСВ /LCВ
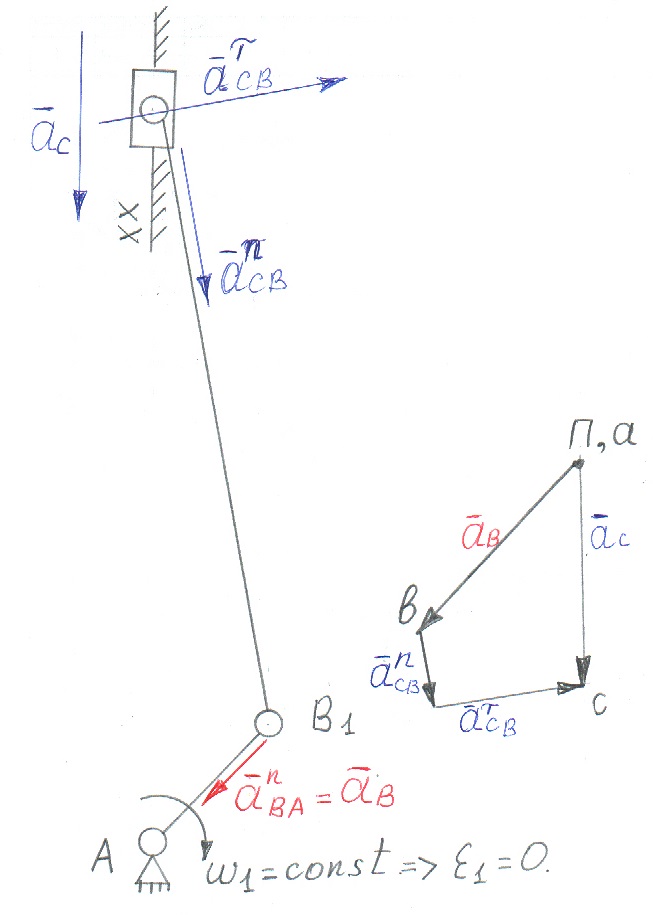
Если мы сложим две составляющие: ɑnСВ и ɑτСВ , то получим полный вектор ɑСВ.

И последнее пояснение. Если нас интересует направление вектора ускорения любой точки механизма и его численное значение, например точки S2, лежащей на шатуне, то мы находим его значение и направление по правилу подобия: «На схеме механизма и плане ускорений изображены подобные фигуры». То есть, если точка S2 делит в какой-то пропорции длину шатуна ВС, то на плане ускорений эта точка будет делить в такой же пропорции отрезок вс. Для определения направления вектора ускорения точки S2 проводим отрезок из полюса Π в точку s2 плана ускорений, это и будет направление вектора ускорения точки S2. Численное значение вектора ускорения точки S2 определяем следующим образом:
ɑS2 = [Π s2 ] х μɑ,
где: [Π s2 ] – отрезок в мм на плане ускорений.
