Задания для практических занятий по теме «Аналитическая геометрия»
Прямая на плоскости
1) Среди прямых  указать параллельные и перпендикулярные.
указать параллельные и перпендикулярные.
2) Прямая  задана точкой
задана точкой  и нормальным вектором
и нормальным вектором  . Составить уравнение этой прямой и привести его к общему виду.
. Составить уравнение этой прямой и привести его к общему виду.
3) Написать уравнение прямой, отсекающей на осях координат отрезки, величины которых соответственно равны 3 и 4.
4) Составить уравнение прямой, проходящей через точки  .
.
5) Определить угловой коэффициент  и отрезок
и отрезок  для каждой из прямых:
для каждой из прямых: 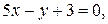


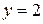 .
.
6) Найти уравнение прямой, образующей с осью  угол
угол  и пересекающей ось
и пересекающей ось  в точке
в точке  .
.
7) Найти расстояние от точки  до прямой
до прямой 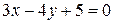 .
.
8) Записать уравнение прямой 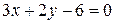 в отрезках, найти точки, в которых прямая пересекает оси координат.
в отрезках, найти точки, в которых прямая пересекает оси координат.
9) Определить острый угол между прямыми  и
и  .
.
10) Составить уравнение прямой, проходящей через точку  и параллельной прямой:
и параллельной прямой:
а)  б)
б)  в)
в) 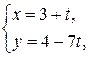 г)
г) 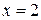 .
.
11) Установить, пересекаются, параллельны или совпадают данные прямые:
а)  и
и 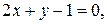 б)
б)  и
и 
в)  и
и 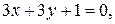 г)
г)  и
и 
12) При каких значениях  прямые
прямые  и
и 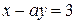 :
:
а) пересекаются, б) параллельны, в) совпадают?
13) Точки  вершины треугольника
вершины треугольника 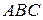 . Написать:
. Написать:
а) уравнение стороны 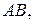 б) уравнение высоты
б) уравнение высоты  и вычислить ее длину, в) уравнение медианы
и вычислить ее длину, в) уравнение медианы 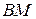 стороны
стороны  , г) найти угол
, г) найти угол  треугольника
треугольника 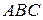 .
.
14) Составить уравнение прямой, проходящей через точку  и перпендикулярной прямой:
и перпендикулярной прямой:
а)  б)
б)  в)
в) 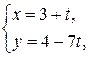 г)
г) 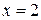 .
.
15) Найти расстояние от точки  до прямой:
до прямой:
а)  б)
б)  в)
в) 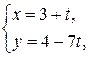 г)
г) 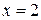 .
.
16) Найти угол между прямыми:
а) 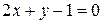 и
и 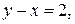 б)
б)  и
и 
в) 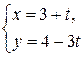 и
и 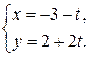
17) Дано общее уравнение прямой 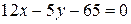 . Написать: а) уравнение с угловым коэффициентом, б) уравнение в отрезках, в) нормальное уравнение.
. Написать: а) уравнение с угловым коэффициентом, б) уравнение в отрезках, в) нормальное уравнение.
18) Определить площадь треугольника, образованного прямой  с осями координат.
с осями координат.
19) Показать, что прямые  и
и 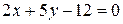 пересекаются, и найти координаты точки пересечения
пересекаются, и найти координаты точки пересечения
Плоскость и прямая в пространстве
1) Составить уравнение плоскости, проходящей через точки 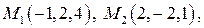
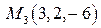 .
.
2) Составить уравнение плоскости, проходящей через точку  и перпендикулярной вектору
и перпендикулярной вектору 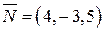 .
.
3) Составить уравнение плоскости, проходящей через точку 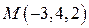 и перпендикулярной плоскостям
и перпендикулярной плоскостям  и
и  .
.
4) Вычислить объем пирамиды, ограниченной плоскостью 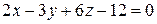 и координатными плоскостями.
и координатными плоскостями.
5) Определить расстояние от точки 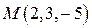 до плоскости
до плоскости 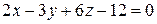 .
.
6) Найти угол между плоскостями 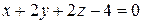 и
и  .
.
7) Даны две точки  и
и 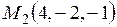 . Составить уравнение плоскости, проходящей через
. Составить уравнение плоскости, проходящей через  перпендикулярно прямой
перпендикулярно прямой 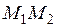 .
.
8) Составить уравнение плоскости, проходящей через точку  параллельно двум векторам
параллельно двум векторам 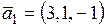 и
и 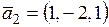 .
.
9) Определить взаимное расположение пар плоскостей:
а) 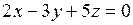 и и  ; ;
|
б)  и и 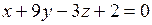 ; ;
|
в) 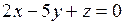 и и  . .
|
10) Найти расстояние от точки  до плоскости
до плоскости 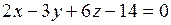 .
.
11) Найти расстояние между параллельными плоскостями:
а) 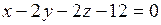 и и  ; ;
|
б) 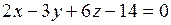 и и 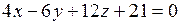 . .
|
12) При каких значениях  и
и  плоскости
плоскости  и
и 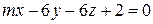 параллельны?
параллельны?
13) При каком значении  плоскости
плоскости  и
и 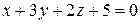 перпендикулярны?
перпендикулярны?
14) Написать уравнение прямой, проходящей через точку  :
:
а) параллельно вектору  ; б) параллельно прямой
; б) параллельно прямой  ;
;
в) параллельно оси 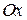 ; г) параллельно оси
; г) параллельно оси  ; д) параллельно прямой
; д) параллельно прямой 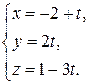
15) Уравнения прямой 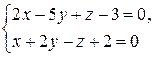 привести к каноническому виду.
привести к каноническому виду.
16) Составить канонические уравнения прямой, проходящей через точки 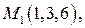
 .
.
17) Составить канонические и параметрические уравнения прямой 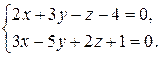
18) Найти угол между прямыми  и
и 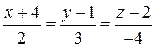 .
.
19) Доказать перпендикулярность прямых  и
и 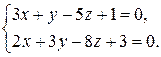
20) Составить канонические уравнения прямой, если она:
а) проходит через две точки  и
и  ,
,
б) проходит через точку  перпендикулярно плоскости
перпендикулярно плоскости  ,
,
в) проходит через точку  параллельно прямой
параллельно прямой 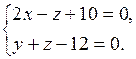
21) Определить взаимное расположение прямых:
а) 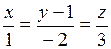 и и 
|
б)  и и 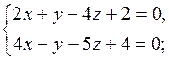
|
в) 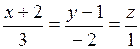 и и 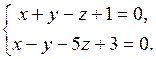
|
22) Найти косинус угла между прямыми  и
и 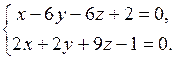
23) Показать, что прямые 
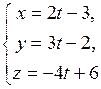 и
и 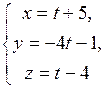 пересекаются, найти координаты точки пересечения.
пересекаются, найти координаты точки пересечения.
24) Показать, что прямая 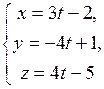 параллельна плоскости
параллельна плоскости  .
.
25) Найти точку пересечения прямой  и плоскости
и плоскости  .
.
26) Найти расстояние от точки 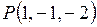 до прямой
до прямой 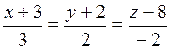 .
.
27) Найти расстояние между прямыми:
а) 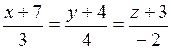 и и  ; ;
|
б) 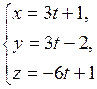 и и 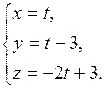
|
28) Доказать, что прямая 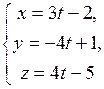 параллельна плоскости
параллельна плоскости  .
.
29) Найти точку пересечения прямой  и плоскости
и плоскости 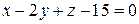 .
.
30) Найти точку пересечения прямой  и плоскости
и плоскости 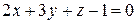 .
.
Кривые на плоскости
1). Составить каноническое уравнение эллипса, если:
а) 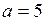 ,
, 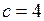 ; б)
; б) 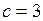 ,
,  ; в)
; в)  ,
,  ; г) большая полуось равна 3, а расстояние между фокусами равно
; г) большая полуось равна 3, а расстояние между фокусами равно  , д) эллипс проходит через точки
, д) эллипс проходит через точки 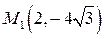 и
и  .
.
2) Составить каноническое уравнение гиперболы, если:
а)  ,
, 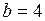 ; б)
; б) 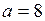 ,
, 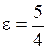 ; в)
; в) 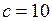 ,
,  – уравнения асимптот; г) мнимая полуось равна 1, а расстояние между фокусами равно
– уравнения асимптот; г) мнимая полуось равна 1, а расстояние между фокусами равно  .
.
3) Написать каноническое уравнение параболы с вершиной в точке (0,0), если:
а) она расположена в левой полуплоскости, симметрична относительно оси Ох и  ;
;
б) если она симметрична относительно оси Оу и походит через точку М (4,–8);
в) если точка F (0,3) – фокус.
4) Найти радиус и координаты центра окружности:
а) 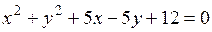 ; б)
; б) 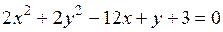 ,
,
в) 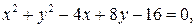 г)
г) 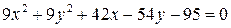 .
.
5) Определить вид кривой второго порядка, заданной уравнением, найти ее центр, координаты вершин, фокусов и эксцентриситет:
а) 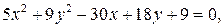 б)
б)  ,
,
в) 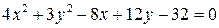 , г)
, г) 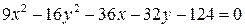 .
.
6) Дано уравнение эллипса 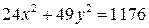 . Найти: длины его полуосей, координаты фокусов, эксцентриситет эллипса, уравнение директрис и расстояние между ними, точки эллипса, расстояние от которых до левого фокуса равно 12.
. Найти: длины его полуосей, координаты фокусов, эксцентриситет эллипса, уравнение директрис и расстояние между ними, точки эллипса, расстояние от которых до левого фокуса равно 12.
7) Дано уравнение гиперболы 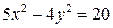 . Найти: длины его полуосей, координаты фокусов, эксцентриситет гиперболы, уравнения асимптот и директрис, фокальные радиусы точки
. Найти: длины его полуосей, координаты фокусов, эксцентриситет гиперболы, уравнения асимптот и директрис, фокальные радиусы точки  .
.
8) Найти координаты вершины и фокуса, уравнение оси и директрисы параболы
а) 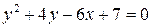 , б)
, б) 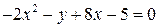 .
.