ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР

1. МЕТОД БРАУНА-РОБИНСОНА (МЕТОД ФИКТИВНОГО РАЗЫГРЫВАНИЯ)

Идея метода: многократное фиктивное разыгрывание игры, когда одна итерация называется партией.

Рассматривается матричная игра Г_А с матрицей А={α_ij}, где .

В первой партии игроки произвольно выбирают свои чистые стратегии.

В k-й партии каждый игрок выбирает ту чистую стратегию, которая максимизирует его ожидаемый выигрыш против наблюдаемого эмпирического вероятностного распределения противника за (k-1) партию. Пусть за k - партий игрок 1 i-ю стратегию использовал -раз, а игрок 2 свою j-ю стратегию использовал -раз.

В (k+1)-й партии игрок 1 будет использовать i_k+1-стратегию, а игрок 2 - j_k+1стратегию. Запишем следующие соотношения:

;

.

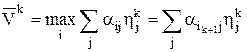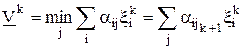Если рассмотреть как соответственно верхнее и нижнее приближённые значения за k- партий, то приближённые оптимальные смешанные стратегии соответственно 1 и 2 го игроков за k- партий можем записать как: 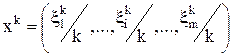и .

Значение игры V находится в диапазоне: .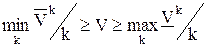

Сходимость представленного алгоритма подтверждается следующей теоремой:

Теорема: .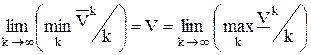

Недостатком данного метода является его медленная и немонотонная сходимость.

Пример. Найти приближённые оптимальные стратегии игроков и значение матричной игры с матрицей . Видим из написанного, что седловой точки нет и значение игры находится в интервале 1<V<2. Стратегии игрока 1 обозначены как α, β, γ, стратегии игрока обозначены как a, b, c.

Вычислительный алгоритм удобнее представить в виде следующей таблицы, в которой на первом шаге взяты первые чистые стратегии игроков:

№ партии	Выбор игрока 1	Выбор игрока 2	Выигрыш игрока 1	Проигрыш игрока 2
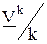
α	β	γ	a	b	c
	α	a
	β	b
	β	b
	γ	b
	γ	b
	γ	b
	γ	b
	γ	c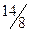
	γ	c
	γ	c
	α	c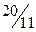
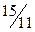
	α	c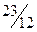

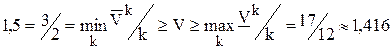
и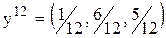

2. МОНОТОННЫЙ АЛГОРИТМ РЕШЕНИЯ МАТРИЧНЫХ ИГР.

Алгоритм позволяет находить (точно и приближённо) оптимальную стратегию 1-го игрока и значение матричной игры V.

Рассматривается матричная игра ГАс матрицей размерности m×n. Обозначим через
- приближённое значение оптимальной стратегии 1-го игрока на N-й итерации. Также введём на N-й итерации как важный элемент нашего алгоритма вспомогательный вектор . Пояснения по его получению будет дано по шагам алгоритма.

Шаг 0: игрок 1 выбирает произвольную свою чистую стратегию i0, т.е. , и вспомогательный вектор строка матрицы А. Приближённое значение игры на шаге 0 будем определять, как
(1) и через (2) обозначим множество тех индексов, для которых выполняется равенство (1).

Замечание: на последующих шагах алгоритма соотношения (1) и (2) будем определять аналогично, лишь изменяя верхний индекс 0 на индекс соответствующего шага, т.е. для N шага эти значения будем обозначать соответственно: V^N, J^N.

Шаг N-1: допустим, что выполнена N-1 итерация и получены x^N-1, c^N-1, V^N-1.

Шаг N: тогда x^N, c^Nвычисляются по следующим формулам:

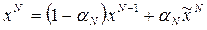(3)

(4),
где , а получение векторов , будем описывать ниже:

Пусть на N шаге рассматривается игра Г^NÌГА c матрицей А^N= , где , т.е. это матрица А только с частью столбцов, определяемых на N-1 шаге по формулам (1) и (2).

Решаем подыгру Г^Nи находим для этой игры оптимальную стратегию 1-го игрока . Вектор определяем по формуле: 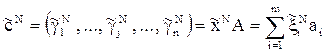, где a_iстроки матрицы А.

Далее решаем (2×n)-игру с матрицей: 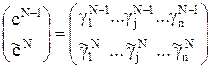(5) и находим для этой игры оптимальную стратегию 1-го игрока (1-α_N, α_N), значения которых подставляем в уравнения (3), (4) для нахождения x^N, c^N.

Вычислительный процесс продолжается до тех пор, пока не будет выполнено условие α_N=0 или не будет достигнута требуемая точность вычисления.

Условие α_N=0 говорит о том, что в матрице (5) первая строка доминирует вторую и, следовательно, в качестве оптимальной стратегии 1-го игрока в исходной задаче можно взять х*= x^N= x^N-1.

Сходимость алгоритма гарантируется следующей теоремой:

Теорема: если - итеративные последовательности, значения которых получаются согласно формулам соответственно (1), (3), тогда выполняются следующих 3 условия:

1. V^N= V^N-1, т.е. последовательность 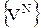монотонно возрастет с ростом итераций;

2. , где V – цена исходной задачи;

3. , х*ÎХ*- оптимальная стратегия первого игрока.

Рассмотрим пример. Дана игра Г_А с платёжной матрицей .

Найти ситуацию равновесия в данной игре.

Решение: шаг 0. В качестве х⁰ выберем первую чистую стратегию 1-го игрока, т.е.
х⁰=(1,0,0) и соответственно в качестве с⁰ выберем первую строку матрицы А:
. Решаем по алгоритму выражение (1): =min(2, 1,3)=1= .
Следовательно (2) J⁰={2}, т.е. второй столбец матрицы А.

Шаг 1. Для нахождения , рассмотрим подыгру Г¹ÌГА c матрицей А¹= , равной второму столбцу матрицы А. Оптимальной стратегией этой игры есть выбор третьей чистой стратегии 1-го игрока, как лучший выигрыш из 1, 0, 2, т.е. =(0,0,1). , т.е. третья строка матрицы А.

Решаем (2×3) игру с матрицей . Так как элементы третьего столбца а³данной матрицы ³ элементов первого столбца а¹, то он доминируем первым столбцом, следовательно его можно убрать из решения, не нарушая спектр оптимальных стратегий. Имеем (2×2) игру с матрицей . Эта игра вполне смешанная, поэтому решая эту игру по известным формулам прямого счёта, получим оптимальную стратегию 1-го игрока (1-α₁, α₁)= .

Так как α₁¹0, то вычисления продолжаем. Вычислим формулы (3) и (4):

;

;

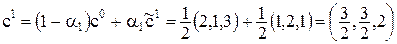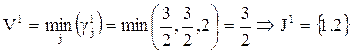, т.е. 1 и 2-й столбцы матрицы А.

Шаг 2. Для нахождения 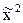, 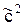рассмотрим подыгру Г²ÌГА c матрицей А²= , равной первому и второму столбцам матрицы А. Так как доминируема и её можно вычеркнуть из спектра оптимальных стратегий. Имеем (2×2) игру с матрицей 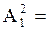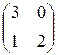. Эта игра вполне смешанная, поэтому решая эту игру по известным формулам прямого счёта, получим для игры с матрицей оптимальную стратегию 1-го игрока = . 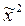Добавлением 0 в качестве первой координаты в получим = оптимальную стратегию 1-го игрока для игры с матрицей А².

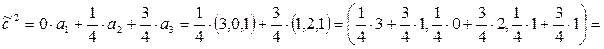
. Решаем (2×3) игру с матрицей а₂доминируема а₁Þ
матрица Þ1-α₂=1 и α₂=0Þвычисления по алгоритму закончены.

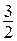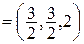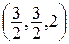
Имеем V=V₁= , х*= x²= x¹= Þ х*А Þ х*Ау*= V 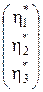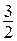Þ

= Þ 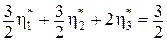, а так как 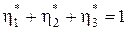Þ

Þу*=(h*,1-h*,0),

где h*Î[0,1].

Самостоятельно решить матричные игры с платёжными матрицами:

и итерационными методами Брауна-Робинсона и монотонным методом, когда по первому методу в матрице А на первом шаге выбрать вторые чистые стратегии игроков, а в матрице В – выбрать четвёртую чистую стратегию 1-го игрока и вторую чистую стратегию 2-го игрока и найти приближённые оптимальные стратегии игроков и интервал, в котором находится значение игры, сделав по 20 итераций. Для второго метода на 0-м шаге в качестве чистой стратегии для матрицы А выбрать третью чистую стратегию 1-го игрока, а для матрицы В четвёртую чистую стратегию 1-го игрока.