РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ

ВЫСШАЯ МАТЕМАТИКА

 

Методические указания

к выполнению расчетно-графической

работы №4 для студентов II курса

очной формы обучения инженерно-

технических специальностей

 

Брянск 2011

УДК 511

 

Высшая математика [Текст]+[Электронный ресурс]: методические указания к выполнению расчетно-графической работы №4 для студентов II курса очной формы обучения инженерно-технических специальностей – Брянск: БГТУ. - 40с.

 

Разработала: ст. преп. Шарашидзе Н.В.

 

Рекомендовано кафедрой «Высшая математика»

(протокол № 3 от 30. 11. 2010.)

 

 

ПРЕДИСЛОВИЕ

 

 

Настоящие методические указания представляют собой подборку задач по теории вероятностей. В них приведены решения типовых задач по темам «Комбинаторика», «Случайные события», «Элементы теории структурной надежности», «Случайные величины». Анализ решений типовых задач призван помочь студентам в самостоятельной работе, а именно, в выполнении домашних заданий и в решении задач расчетно-графической работы.

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

 

1. Вентцель, Е.С. Теория вероятностей/Е.С. Вентцель, Л.А. Овчаров. – М.: Наука, Физматлит. 1973-365с.

2. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие/В.Е. Гмурман. – М.: Высш.шк., 2003. – 405с.

3. Коршунов, Д.А. Сборник задач и упражнений по теории вероятностей: учеб.пособие/ Д.А. Коршунов, С.Г. Фосс, И.М., Эйсымонт. – СПб.: Лань, 2004. – 192с.

 

 

КОМБИНАТОРИКА

 

Область математики, в которой решается вопрос о том, сколько различных комбинаций можно составить из данного множества, называется комбинаторикой.

Приведем примеры комбинаторных задач и их решения:

1.1. Из города А в город В ведут три различные дороги, а из города В в город С ведут 5 различных дорог. Сколькими различными способами можно добраться из города А в город С при условии, что из А в С можно добраться только через город В?

Решение. Из А в В можно добраться 3 способами и для каждого из них существует 5 способов добраться из В в С. Значит, из А в С можно добраться 3×5=15 способами.

Ответ: 15.

Здесь каждый последующий выбор осуществляется для каждого способа предыдущего выбора, поэтому количество способов перемножается.

Правило произведения формулируется так: Если некоторый выбор можно осуществить k способами и для каждого из этих способов второй можно осуществить n способами, то общее число способов осуществления выборов равно k×n.

1.2. У юноши 5 брюк, 6 рубашек и 3 куртки. Он выбирает 1 брюки, 1 рубашку и 1 куртку. Сколько у юноши есть способов одеться?

Решение. Одну пару брюк из 5 можно выбрать 5 способами и для каждого из них есть 6 способов выбрать рубашку. То есть общее число способов выбора брюк и рубашки равно 5×6=30, и для каждого из них есть 3 способа выбрать куртку. Значит, общее число способов одеться равно 5×6×3=90.

Ответ: 90.

1.3. В спортивном турнире участвуют 10 команд. Сколькими способами могут быть разделены между ними четыре призовых места?

Решение. Первое место может занять любая команда из 10 – 10 способов. Второе место – любая из оставшихся девяти команд – 9 способов. Третье место – любая из оставшихся команд – 8 способов и, наконец, четвертое место может занять любая из семи команд – 7 способов. Общее число способов 10×9×8×7=5040.

Ответ: 5040.

В задаче 1.3 мы составляли группы из команд: эти группы отличались друг от друга либо составом команд, либо порядком их следования.

Размещения

 

Определение. Множества, отличающихся друг от друга элементами или порядком их следования, называются размещениями, их количество обозначается так: , где n – число элементов в множестве, из которого мы выбираем, m – число элементов в множестве, которое выбираем, т.е. m £ n.

Общая формула имеет вид:

m £ n.

Перестановки

Рассмотрим множество, содержащее n элементов, и будем из него составлять n – элементные множества, отличающиеся друг от друга только порядком следования элементов. Такие множества называются перестановками, их количества обозначают P_n.

Ясно, что P_n= .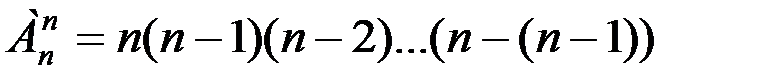

Произведение последовательных натуральных чисел от 1 до n обозначают n!(n – факториал).

Итак, P_n= 1×2×3×…×(n -2)×(n -1)× n = n!

Например, список студентов группы из 20 человек можно составить 20! способами. Число размещений определяем по формуле .

Сочетания

1.4. Сколькими способами из 20 человек можно выбрать двух дежурных?

Решение. В этой задаче не важен порядок выбора. Общее число упорядоченных пар (число размещений) равно 20×19; ясно, что количество неупорядоченных пар вдвое меньше, и равно . Заметим, что 2- это число перестановок в множестве из двух элементов. Если бы мы выбирали 3-х дежурных из 20, то делить нужно было бы на 3!=6, т.е. формула имела бы вид .

Ответ: 1140.

В задаче 1.4 мы встретились с множествами, отличающимися друг от друга, по крайней мере, одним элементом, но никак не порядком их следования. Такие множества называются сочетаниями. Их количество обозначается и определяется по формуле .

Например,

- любые 2 карты из 36 можно выбрать способами;

- любых 4 человек из 8 можно выбрать 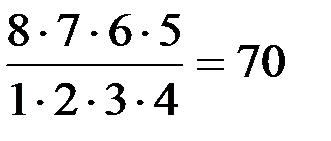способами;

- любые 3 точки из 10 данных можно выбрать способами.

1.5. Сколькими различными способами можно заполнить карточку «Спортлото», если из 49 клеток надо выбрать 6?

.

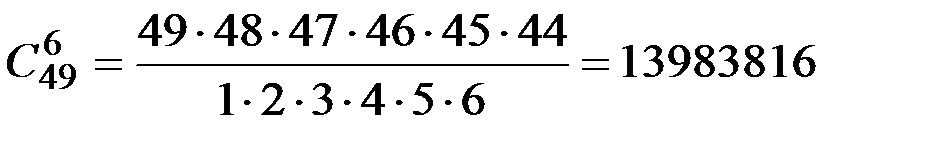Ответ: 13983816.

1.6. В партии из 50 изделий 2 бракованных. Сколькими способами можно выбрать наудачу 3 изделия, среди которых ровно одно окажется бракованным?

Решение. Одно бракованное изделие из двух можно выбрать двумя способами и после каждого такого выбора два доброкачественных изделия из 48 можно выбрать различными способами. Значит всего будет троек изделий , в каждом из которых одно бракованное.

= .

Ответ: 2256.

Замечание. Во всех приведенных примерах элементы в множествах не повторялись.

 

СЛУЧАЙНЫЕ СОБЫТИЯ

 

2.1. Брошены две игральные кости.

События:

А – на первой кости выпало нечетное число,

В – на второй кости выпало нечетное число,

С – сумма цифр на обеих костях нечетна.

Проверьте, зависимы или нет события А, В и С: а) попарно; б) в совокупности.

Решение. Применим классическую схему с 36 равновозможными исходами, которые удобно представить клетками в таблице 6 х 6 (табл.1). Отметим клетки, благоприятствующие А, В и С, соответствующими буквами.

Таблица 1

I II
	АВ	ВС	АВ	ВС	АВ	ВС
	АС		АС		АС
	АВ	ВС	АВ	ВС	АВ	ВС
	АС		АС		АС
	АВ	ВС	АВ	ВС	АВ	ВС
	АС		АС		АС

Всего исходов n =36.

Появлению события А благоприятствует 18 случаев, n_А =18, событию В – 18 случаев, событию С – 18 случаев, n_В =18, n_С =18. По определению вероятности события в классической схеме ; ; . Событию АВ благоприятствует 9 случаев, n_АВ =9; событию ВС – 9 случаев, n_ВС =9; событию АС – 9 случаев, n_АС =9. Следовательно, ; ; . Проверим, выполняется ли условие независимости событий А и В; В и С; А и С:

Р(АВ)=Р(А)Р(В), Р(ВС)=Р(В)Р(С), Р(АС)=Р(А)Р(С). Все три равенства выполнены , что означает попарную независимость событий А, В и С. Для независимости же в совокупности необходимо выполнение равенства Р(АВС)=Р(А)Р(В) Р(С). Р(АВС)= 0, так как если на обеих костях нечетные цифры, то их сумма четна и, следовательно, АВС – невозможное событие. Р(А)Р(В)Р(С) = . Независимости в совокупности нет.

Ответ: события попарно независимы; независимости в совокупности нет.

2.2. Из урны, содержащей 12 белых и 8 черных шаров, наудачу извлекают один шар. Какова вероятность извлечь наудачу из урны белый шар?

Решение. А – событие, состоящее в том, что извлеченный шар оказался белым. Применим классическое определение вероятности, получим , где n =20, m =12. Р(А)= 12/20=3/5.

Ответ: 3/5.

2.3. Из урны, содержащей 12 белых и 8 черных шаров, один шар неизвестного цвета утерян. Какова вероятность извлечь наудачу из урны белый шар?

Решение. Пусть Н ₁ – событие, состоящее в том, что утерян белый шар; Н ₂ – событие, состоящее в том, что утерян черный шар; А – событие, состоящее в том, что шар, извлеченный из оставшихся шаров, оказался белым. 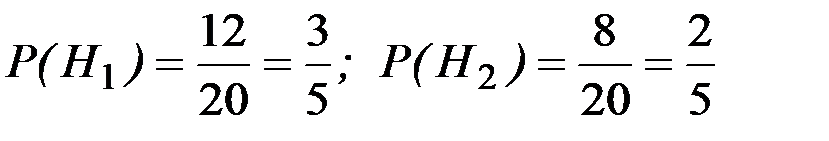. Если утерян белый шар, то в урне осталось 11 белых и 8 черных шаров, следовательно, условная вероятность события А равна . Если утерян черный шар, то в урне осталось 12 белых и 7 черных шаров, следовательно, условная вероятность события А равна . По формуле полной вероятности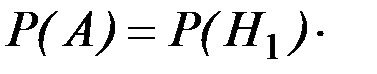

.

Отметим, что вероятность извлечения белого шара из урны до утери шара тоже равна 3/5.

Ответ: 3/5.

2.4. В первой урне 3 белых и 4 черных шара, а во второй – 2 белых и 3 черных шара. Из первой урны переложили во вторую два шара. Найдите вероятность того, что шар, вынутый из второй урны после перекладывания, окажется белым.

Решение. Обозначим события:

А – шар, взятый из второй урны после перекладывания, – белый;

Н ₁ – во вторую урну добавили 2 белых шара;

Н ₂ – во вторую урну добавили 1 белый и 1 черный шар;

Н ₃ – во вторую урну добавили 2 черных шара.

Вероятности событий Н ₁, Н ₂, Н ₃:

После перекладывания во вторую урну двух белых шаров в ней окажется 4 белых и 3 черных шара; одного белого и одного черного – 3 белых и 4 черных; двух черных шаров – 2 белых и 5 черных, поэтому условные вероятности события А равны

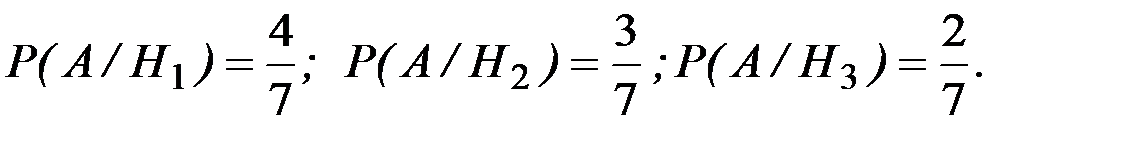По формуле полной вероятности

Ответ: 0,408.

2.5. В первом ящике находятся 3 белых и 4 черных шара, во втором – 5 белых и 3 черных шара. Из каждого ящика случайным образом извлекли по два шара и положили в третий ящик. Какова вероятность того, что шар, взятый из третьего ящика, будет белым?

Решение. Обозначим события:

А ₁ – из первого ящика удалили 2 белых шара;

А ₂ – из первого ящика удалили 1 белый и 1 черный шар;

А ₃ – из первого ящика удалили 2 черных шара;

В ₁ – из второго ящика удалили 2 белых шара;

В ₂ – из второго ящика удалили 1 белый и 1 черный шар;

В ₃ – из второго ящика удалили 2 черных шара;

С – шар, взятый из третьего ящика, – белый.

Вероятности событий А ₁, А ₂, А ₃, В ₁, В ₂, В ₃.

События Н ₁= А ₁ В ₁, Н ₂= А ₁ В ₂, Н ₃= А ₁ В ₃, Н ₄= А ₂ В ₁, Н ₅= А ₂ В ₂, Н ₆= А ₂ В ₃, Н ₇= А ₃ В ₁, Н ₈= А ₃ В ₂, Н ₉= А ₃ В ₃ образуют полную группу событий, их вероятности равны:

События:

Н ₁ –в третьем ящике 4 белых шара;

Н ₂ –в третьем ящике 3 белых и 1 черный шар;

Н ₃ –в третьем ящике 2 белых и 2 черных шара;

Н ₄ –в третьем ящике 3 белых и 1 черный шар;

Н ₅ –в третьем ящике 2 белых и 2 черных шара;

Н ₆ –в третьем ящике 1 белый и 3 черных шара;

Н ₇ –в третьем ящике 2 черных и 2 белых шара;

Н ₈ –в третьем ящике 1 белый и 3 черных шара;

Н ₉ –в третьем ящике 4 черных шара.

Условные вероятности события С:

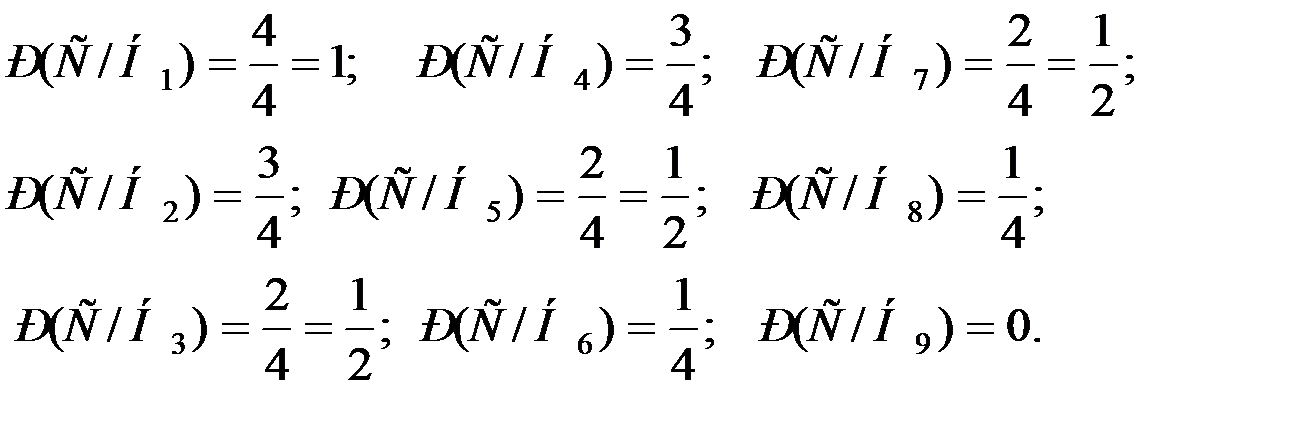
По формуле полной вероятности

Ответ: 0,527.

2.6. Надежности элементов системы соответственно равны 0,6; 0,7; 0,8; 0,9. В результате эксплуатации система отказала. Найдите вероятность того, что отказали только элементы с номерами 1 и 2 (рис.1).

Решение. Обозначим события:

Н – отказали только элементы с номерами 1 и 2,

Рис.1

А – система отказала.

Для вычисления вероятности, воспользуемся формулой Бейеса:

Р(А/Н) =1.

Р(Н)=q ₁× q ₂× р ₃× р ₄ =

=0,4×0,3×0,8×0,9=0.0864.

Надежность системы равна = =(1-0,4×0,44)0,9=0,824×0,9=0,7416.

Р(А)= 1-0,7416=0,2584.

Следовательно, .

Ответ: 0,334.

2.7. Надежности элементов системы соответственно равны 0,8; 0,7; 0,6; 0,9; 0,8. Элемент 5 можно дублировать. Имеются четыре резервных элемента с такой же надежностью. Сколько достаточно поставить дублирующих элементов, чтобы повысить надежность на 20%. На сколько процентов повысится надежность системы, если использовать для дублирования все имеющиеся резервные элементы? (рис.2).

Рис.2

Решение. Найдем надежность исходной системы

Р _1,2=1- q _1,2=1-0,2×0,3=0,94; Р _3,4=1- q _3,4=1-0,4×0,1=0,96; P _I= Р _1,2× Р _3,4× Р ₅ =0,94×0,96×0,8=0,72192.

Найдем надежность системы, если поставить один дублирующий элемент:

P _II= Р _1,2× Р _3,4· (1- q ₅× q ₅)=0,94×0,96×0,96=0,866304.

следовательно, чтобы повысить надежность системы на 20%, достаточно поставить один дублирующий элемент. Найдем надежность системы, если поставить все резервные элементы.

P _III= Р _1,2× Р _3,4 (1- q ₅× q ₅× q ₅ × q ₅× q ₅)=0,94×0,96×0,99968=0,902.

. Надежность системы повысится на 25%.

Ответ: один элемент; на 25%.

 

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

 

3.1. Электроприбор состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна р =0,1. 1. Составьте закон распределения числа отказавших элементов в одном опыте. 2. Постройте график функции распределения случайной величины.

Решение. Дискретная случайная величина Х – число отказавших в одном опыте элементов – может принимать значения:

х₁ =0 (ни один элемент электроприбора не отказал);

х ₂=1 (отказал ровно один элемент);

х ₃=2 (отказали ровно два элемента);

х ₄=3 (отказали все три элемента).

Для отыскания соответствующих вероятностей р ₁, р ₂, р ₃, р ₄ применима формула Бернулли, так как отказы элементов независимы друг от друга и вероятности отказа каждого элемента равны между собой

Имеем: n =3, p =0,1, q =1-0,1=0,9. И далее:

р ₁= р ₃(0)= ;

р ₂= р ₃(1)= ;

р ₃= р ₃(2)= ;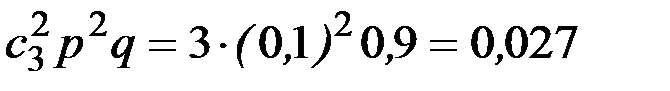

р ₄= р ₃(3)= .

(Контроль: р ₁+ р ₂+ р ₃+ р ₄=0,729+0,243+0,027+0,001=1). Искомый закон распределения дискретной случайной величины Х:

 

Х
р	0,729	0,243	0,027	0,001

 

Построим график функции распределения (рис.3).

0,999

0,972

0,729

F(x)

х

Рис.3

3.2. Преподаватель на экзамене задает студенту вопросы. Вероятность того, что студент ответит на любой вопрос, равна 0,9. Преподаватель прекращает экзамен, как только студент не сможет ответить на очередной заданный вопрос. Составьте закон распределения дискретной случайной величины Х – числа вопросов, которые преподаватель задаст студенту. Найдите число заданных преподавателем вопросов, имеющее наибольшую вероятность.

Решение. Число заданных дополнительных вопросов есть дискретная случайная величина Х, принимающая следующие возможные значения: х ₁=1, х ₂=2, х ₃=3, …, х_k = k и т.д.

Будем искать вероятности этих возможных значений. Экзаменатор задает только один дополнительный вопрос, если студент не ответит на первый вопрос. Вероятность этого возможного значения равна 1-0,9=0,1, т.е. р(х ₁)= р (1)=0,1.

Экзаменатор задаст два дополнительных вопроса, если студент ответит на первый вопрос (вероятность 0,9), но не ответит на второй (вероятность 0,1). Таким образом, р(х ₂)=0,09. Рассуждая аналогично, найдем

р(Х ₁)=0,9×0,9×0,1=0,081,

…

р(х_k) =(0,9) ^{k -1}×0,1.

Запишем искомый закон распределения:

 

Х				…	k	…
р	0,1	0,09	0,081	…	(0,9) k -1×0,1	…

 

Отсюда видно, что наивероятнейшее число заданных студенту дополнительных вопросов равно 1.

Ответ: 1.

3.3 Из орудия ведется стрельба по цели до первого попадания. Вероятность попадания в цель при первом выстреле равна 0,3, при каждом следующем увеличивается на 0,1. Составьте закон распределения числа истраченных снарядов, если имеется 5 снарядов. Найдите числовые характеристики данной случайной величины и постройте график ее функции распределения.

Решение. Случайная величина Х – число истраченных снарядов, ее возможные значения 1,2,3,4,5. Вероятность попадания в цель при первом выстреле р ₁=0,3. Если истрачено 2 снаряда, то это означает, что первый не достиг цели, а второй – попал и р ₂=0,7×0,4=0,28. Если истрачено 3 снаряда, то это означает, что первый и второй не достигли цели, а третий – попал и р ₃=0,7×0,6×0,5=0,21. Аналогично, р ₄=0,7×0,6×0,5×0,6=0,126. р ₅=1-(р ₁+ р ₂+ р ₃+ р ₄)=1-(0,3+0,28+0,21+0,126)= =0,084.

Закон распределения случайной величины Х имеет вид

 

Х
р	0,3	0,28	0,21	0,126	0,084

 

Найдем математическое ожидание случайной величины Х по формуле М[X] = х ₁ р ₁+ х ₂ р ₂+ х ₃ р ₃+ х ₄ р ₄+ х ₅ р ₅=1×0,3+2×0,28+3×0,21+

+4×0,126+5×0,084=2,414. Найдем дисперсию D[X] по формуле

D[X]=М[X ² ] - (М[X]) ²=1²×0,3+2²×0,28+3²×0,21+4²×0,126+5²×0,084- -

-2,414²=7,426-2,414=1,6.

0,916

0,79

0,58

0,3

F(x)

х

Рис.4

Среднее квадратическое отклонение s[ X ] находим по формуле

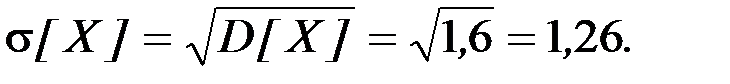График функции распределения случайной величины Х имеет вид (рис.4).

Ответ: М[X] =2,414;

D[X]= 1,6; s[ X ]=1,26.

 

 

3.4. На факультете 730 студентов. Вероятность рождения каждого студента в данный день равна 1/365. Найдите наиболее вероятное число студентов, родившихся 1 января, и вероятность того, что найдутся 3 студента с одним и тем же днем рождения. (Указание: используйте локальную теорему Муавра-Лапласа).

Решение. .

На основании локальной теоремы Муавра-Лапласа имеем

Ответ: 2; 0,22.

3.5. Если в среднем левши составляют 1%, каковы шансы на то, что среди 200 человек а) окажется ровно четверо левшей; б)найдется четверо левшей.

Решение. а) . Используя формулу Пуассона, найдем l=np =2, т.е.

б)

.

Ответ: 0,09; 0,15.

3.6. Поток сбоев, возникающих при работе автоматической линии, можно считать простейшим. Среднее число неисправностей за месяц равно 1,5. Определите вероятность сбоя в работе автоматической линии за 8 дней. Найдите среднее время безотказной работы.

Решение. Так как поток отказов является простейшим, то время Т безотказной работы распределено по показательному закону с параметром сбоев в сутки. Тогда вероятность отказа за 8 дней работы равна

.

Ответ: 0,33.

3.7. При 14400 бросаниях монеты герб выпал 7428 раз. Какова вероятность такого или еще большего уклонения числа выпадений герба при np =14400(1/2)=7200 (монета симметрична и р =1/2)?

Решение. При больших n закон распределения биномиальной величины с параметрами n и р близок к нормальному с параметрами а=np= 7200, 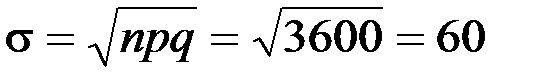. Х – число выпадений герба, а вероятность отклонения от математического ожидания не более чем на g равна

Ответ: 0,00014.

3.8. В страховом обществе застраховано 10000 лиц одного возраста и одной социальной группы. Вероятность случайной травмы в течение года для каждого лица равна 0,006. Каждый застрахованный вносит 1 января 1200 рублей страховых и в случае травмы получает от страхового общества 100 000 рублей. Найдите вероятность того, что а) страховое общество потерпит убыток;

б) страховое общество получит прибыль, не меньшую 4 млн руб., 6 млн руб., 8 млн руб.

Решение. а) Все взносы на 1 января составляют 12 млн рублей; в случае получения травмы в течение года 120 человек все компенсации также составят 12 млн рублей. Следовательно, вероятность убытков для страховщиков есть при получении травмы в течение года более 120 человек. Х – число лиц, получивших травму в течение года – биномиальная случайная величина с параметрами n =10 000, р =0,006; q= 0,994; np =60;

Применим интегральную теорему Лапласа:

(с точностью более чем до 10-го знака после запятой).

б) Получение прибыли в 4 млн рублей и более может быть, если в течение года получат травмы не более 80 человек (12млн-8млн= =4млн).

Прибыль в 6 млн рублей и более может быть, если в течение года получат травмы не более 60 человек (12млн-6млн=6млн).

Прибыль в 8 млн рублей и более может быть, если в течение года получат травмы не более 40 человек (12млн-4млн=8млн).

Ответ: а)0; б) 0,99534; 0,5; 0,0047.

РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ

Задание 1

Вариант 1. Брошено три монеты. Найти вероятности событий: А- выпадение герба на первой монете; В - выпадение ровно двух гербов. Зависимы ли события А и В?

Вариант 2. В первой урне 2 белых и 3 черных шара. Во второй урне 3 белых. Из каждой удалили по одному, наугад взятому шару, а оставшиеся шары поместили в третью урну (пустую). Какова вероятность события А - шар наугад взятый из 3-й урны, белый?

Вариант 3. Из 20 лотерейных билетов 4 выигрышных. Три человека по очереди берут по одному билету. Найти вероятности событий: А1 - первый возьмет выигрышный; А2 - второй возьмет выигрышный.

Вариант 4. В первой урне 1 белый и 4 черных шара, во второй - 1 белый и 2 черных. В первую урну добавили один шар, наугад взятый из второй урны. После этого из 1-й урны наугад извлекли 1 шар. Какова вероятность того, что этот шар белый.

Вариант 5. Игральная кость брошена 2 раза. Х1 - количество очков при первом бросании; Х2 - количество очков при втором бросании. События: А={Х1 делится на 2}; В={Х2 делится на 2}. Найти вероятность произведения АВ. Зависимы ли события А и В?

Вариант 6. Из урны, содержащей 2 белых и 2 черных шара, извлекают по одному без возвращения все шары. Найти вероятности событий: 1) третий шар белый, 2) третий и четвертый шары белые, 3) четвертый - белый, при условии, что третий был белым.

Вариант 7. В первой урне 1 белый и 2 черных шара, во второй - 2 белых и 3 черных. Из первой и второй урн взяли наугад по одному шару и поместили в третью (пустую) урну. Какова вероятность того, что взятый наугад из 3-й урны шар окажется белым?

Вариант 8. Игральная кость брошена два раза. Х1 - количество очков при первом бросании; Х2- количество очков при втором бросании. События: А={Х1 делится на 2}; В={Х2 делится на 3}. Найти вероятности: Р(А), Р(В), Р(АВ). Зависимы ли события А и В?

Вариант 9. Из пяти карточек с номерами 1,2,3,4,5 наугад извлекают одну, регистрируют ее номер Х, а карточку возвращают в общую совокупность. После этого вторично извлекают наугад карточку и регистрируют ее номер Y. Какова вероятность того, что хотя бы одно из чисел Х, Y равно 3, если Х+Y - четное число?

Вариант 10. Брошены две игральные кости. События: А={число очков на 1-й кости делится на 2}; В={ сумма очков, выпавших на 1-й и 2-й костях делится на 4}. Зависимы ли события А и В? Найти вероятности: Р(А), Р(В), Р(АВ), Р(В/А), Р(А/В).

Вариант 11. Из ящика, содержащего три билета с номерами 1,2,3, извлекают по одному все билеты. Предполагая, что все последовательности номеров билетов имеют одинаковые вероятности, найти вероятность того, что хотя бы у одного билета порядковый номер совпадет с его собственным номером.

Вариант 12. Имеется 5 урн с шарами. В 1-й, 2-й и 3-й содержатся по 2 белых и по одному черному, а в 4-й и 5-й - по одному белому и одному черному. Наугад выбирается одна урна и из нее берут наугад один шар. Какова вероятность того, что этот шар белый?

Вариант 13. Игральная кость брошена 2 раза. Х1 и Х2 - количество очков, выпавших при первом и втором бросании. События: А={Х1 делится на 2, Х2 делится на 4}; В={Х1 делится на 3}. Зависимы ли события А и В?

Вариант 14. В первой урне находятся 2 белых и 3 черных шара, во второй урне - 3 белых и 2 черных. Из первой урны во вторую переложили один шар. После этого извлекли наугад один шар из второй урны. Какова вероятность того, что этот шар белый?

Вариант 15. Игральная кость брошена 2 раза. Х1 и Х2 - количество очков, выпавших на верхних гранях. События: А={6£Х1 + Х2 £ 8}; В={Х1 - четное число}. Зависимы ли события А и В?

Вариант 16. В первой урне содержатся 4 белых и 2 черных шара, во второй - 2 белых и 4 черных. Из первой урны переложили во вторую один шар, а затем из второй урны переложили в первую урну один шар, и взяли из 1-й урны наугад 1 шар. Какова вероятность того, что этот шар черный?

Вариант 17. Игральная кость брошена 2 раза. Х1 и Х2 - количество очков, выпавших на верхних гранях. События: А={-2£Х1 - Х2 £2}; В={Х1 = Х2}. Зависимы ли события А и В? Найти вероятности: Р(А), Р(В), Р(АВ), Р(В/А).

Вариант 18. Брошены две игральные кости. Х1 - количество очков, выпавших на 1-й кости; Х2 - количество очков, выпавших на 2-й кости. События: А={Х1 делится на 3}; В={Х1 +Х2 ³10}. Зависимы ли события А и В? Найти вероятности: Р(А), Р(В), Р(АВ), Р(А/В).

Вариант 19. Из урны, содержащей 2 белых и 2 черных шара, извлекли 1 шар наугад, а затем добавили 2 белых и 1 черный. Какова вероятность того, что извлеченные после этого 2 шара окажутся оба белыми?

Вариант 20. Из урны, содержащей 2 белых и 1 черный шар, извлекают по одному все шары. Какова вероятность того, что 3-й шар окажется белым?

Вариант 21. Из урны, содержащей 3 шара с номерами 1,2,12, извлекают наугад один шар. Ак - {на извлеченном шаре содержится цифра к} (к=1,2) Зависимы ли события А1, А2?

Вариант 22. Из урны, содержащей 2 белых и 3 черных шара, наугад извлекли 2 шара, а затем добавили один черный шар. Какова вероятность того, что извлеченный после этого наугад шар окажется белым?

Вариант 23. Из урны, содержащей 2 белых и 4 черных шара, удалили два наугад, а затем извлекли 3-й шар. Какова вероятность того, что этот шар белый?

Вариант 24. В первой урне 4 белых и 2 черных шара, во второй 2 белых и 4 черных. Из первой урны переложили во вторую один шар. После этого из второй урны извлекли один шар. Какова вероятность того, что шар, взятый из 2-й урны, черный?

Вариант 25. Имеются 3 урны с шарами. В 1-й и 2-й по 2 белых и 3 черных шара. В 3-й урне белых шаров столько же, сколько и черных. Найти вероятность того, что извлеченный из наугад взятой урны шар окажется белым. Шар оказался черным. Какова вероятность того, что он извлечен из 3-й урны?

Вариант 26. В ящике имеются 10 шаров: 6 белых и 4 черных. Три шара имеют метку, в том числе 2 белых. Наугад извлекают один шар. Зависимы ли события: А - шар имеет метку; В - шар белый? Найти вероятность того, что шар белый при условии, что он имеет метку.

Вариант 27. Наугад извлекают 1 шар из ящика, содержащего 15 шаров, причем, 6 из них белых; 5 шаров имеют метку, в том числе 2 белых имеют метку. Зависимы ли события: А - шар белого цвета; В - шар имеет метку? Найти вероятность события А при условии, что событие В произошло.

Вариант 28. Из 25 экзаменационных билетов 5 «хороших». Два студента берут по очереди по одному билету. Найти вероятности событий: А - 1-й студент взял «хороший» билет; В - 2-й студент взял «хороший» билет; С - оба студента взяли «хорошие» билеты.

Вариант 29. Брошены 2 игральные кости. Х1 - количество очков, выпавших на 1-й кости; Х2 - количество очков выпавших на 2-й кости. События: А={Х1 - четно и Х2 - четно}; В={6£Х1+Х2£8}. Зависимы ли события А и В? Найти вероятности: Р(А), Р(В), Р(В/А).

Вариант 30. Из группы студентов наугад отбирают одного. В группе 20 студентов, из них 8 курящих, 5 носят очки, х студентов и курят, и носят очки. При каком значении х события: А - студент курящий; В - студент носит очки независимы?

Вариант 31. В группе из 25 человек 15 юношей и 10 девушек. 7 из 25 старше 19 лет, в том числе 3 девушки. Наугад выбран один из группы. Зависимы ли события А и В, где А - выбран юноша, В - выбран человек старше 19 лет? Найти вероятность Р(В/А).

Вариант 32. Игральная кость брошена два раза. Х1 - количество очков при первом бросании; Х2 - количество очков при втором бросании. События: А={Х1 +Х2=7}; В={|X1- Х2 | =3}. Зависимы ли события А и В? Найти условные вероятности: Р(А/В), Р(В/А).

Задание 2

1.

Система может работать в двух режимах: благоприятном и неблагоприятном. Вероятности отказов элементов соответственно равны при благоприятном режиме 0,1; 0,05; 0,2; 0,1, при неблагоприятном режиме 0,2; 0,1; 0,3; 0,2. Определить надёжность системы, если в неблагоприятном режиме система работает 20 % времени.

2.

Определить надёжность системы. Надёжности элементов соответственно равны 0,8; 0,9; 0,8; 0,6, 0,7; 0,9.

3.

Надёжности элементов системы соответственно равны 0,8; 0,7; 0,9. В результате эксплуатации система отказала. Найти вероятность того, что отказал только элемент с номером 3.

4.

Надёжности элементов системы соответственно равны 0,8; 0,7; 0,9; 0,6; 0,8. На сколько процентов повысится надёжность системы, если элементы 4 и 5 дублировать такими же элементами (каждый элемент дублируется отдельно)? Поделиться: Поиск по сайту ©2015-2024 poisk-ru.ru Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-02-13 Нарушение авторских прав и Нарушение персональных данных

 Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд Тема 11. Банковские риски и способы их оценки Опросник «Активность повседневной жизни» Интересно: Глава 3.Что такое успех? Что такое современная опера Что такое графический способ записи алгоритмов? Роль музыки в эстетическом воспитании Обратная связь