ОТВЕТЫВАРИАНТ №8 ДОП
Вариант № 16323675
1. Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Американская миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 39 миль в час? Ответ округлите до целого числа.
Решение.
Спидометр показывает скорость 39 миль в час, значит, в километрах скорость автомобиля составит 
км в час.
Ответ: 63.
2. 
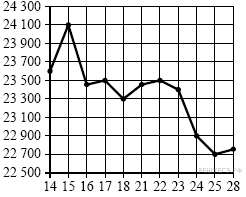На рисунке жирными точками показана цена олова на момент закрытия биржевых торгов во все рабочие дни с 14 по 28 июля 2008 года. По горизонтали указываются числа месяца, по вертикали — цена тонны олова в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена олова на момент закрытия торгов была наименьшей за данный период.
Решение.
Из графика видно, что наименьшей цена была 25 июля (см. рисунок).
Ответ: 25.
3. 
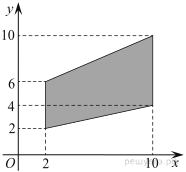Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (10; 4), (10; 10), (2; 6).
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту. Основания трапеции равны 4 и 6. Высота трапеции равна 10 − 2 = 8. Поэтому
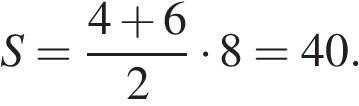
Ответ: 40.
4. В сборнике билетов по математике всего 20 билетов, в 11 из них встречается вопрос по теме "Логарифмы". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Логарифмы".
Решение.
Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам, равна
Ответ: 0,55.
5. Найдите корень уравнения 
Решение.
Возведем обе части уравнения в пятую степень:
Ответ: −29.
6. 
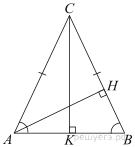В треугольнике 
, 
Найдите высоту 
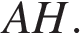
Решение.
Треугольник равнобедренный, значит, углы 
и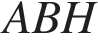 
равны как углы при его основании, а высота, проведенная из точки 
, делит основание 
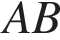пополам.
Ответ: 7,5.
7. 
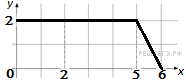На рисунке изображён график некоторой функции 
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите 
, где 
— одна из первообразных функции 
Решение.
Разность значений первообразной в точках 6 и 2 равна площади выделенной на рисунке трапеции 
Поэтому
Ответ:7.
8. 
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 5, 4, 1 и двух площадей квадратов со стороной 2:
Ответ: 50.
9. Найдите значение выражения 
при 
Решение.
Поскольку 
, имеем:
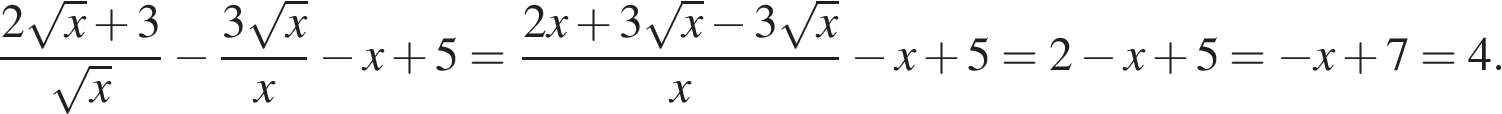
Ответ: 4.
10. Груз массой 0,2 кг колеблется на пружине. Его скорость v меняюется по закону 
где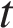 
— время с момента начала колебаний, T = 2 с — период колебаний, 
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле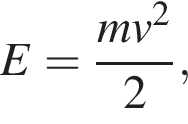 
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 40 секунд после начала колебаний. Ответ дайте в джоулях.
Решение.
Найдем скорость груза через 40 секунд после начала колебаний:
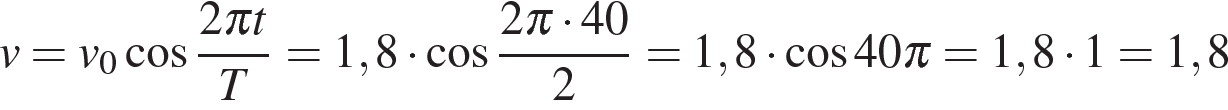
Найдем кинетическую энергию груза через 40 секунд после начала колебаний:
Ответ: 0,324
11. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 70 км/ч и 50 км/ч. Длина пассажирского поезда равна 800 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 45 секундам. Ответ дайте в метрах.
Решение.
Скорость сближения поездов равна: 
км/ч, что составляет 
м/с.
За 45 секунд один поезд проходит мимо другого, то есть вместе поезда преодолевают расстояние, равное сумме их длин:
м.
Следовательно, длина скорого поезда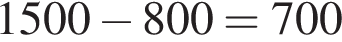 
м.
Ответ: 700.
12. Найдите наибольшее значение функции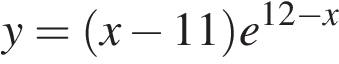 
на отрезке 
Решение.
Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
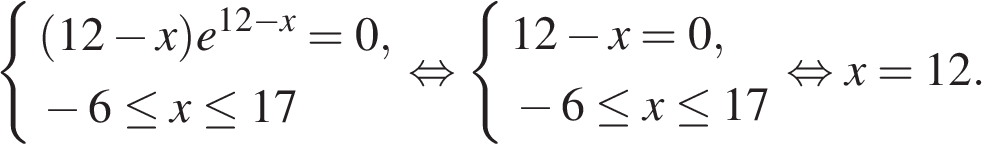
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке 
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
Ответ: 1.
13. а) Решите уравнение: 
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение.
а) Пусть 
тогда поскольку 
и 
, получаем:
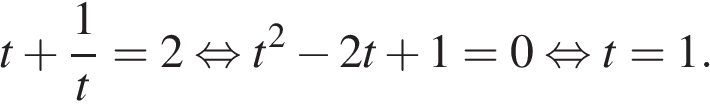
Тогда:
б) Найдём корни, лежащие на заданном отрезке:
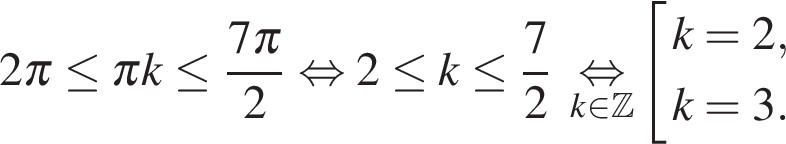
Тем самым, отрезку 
принадлежит корни 
и 
Ответ: а) 
б) 
Приведём другое решение.
В силу неравенства между средним арифметическим и средним геометрическим, имеем:
Тогда
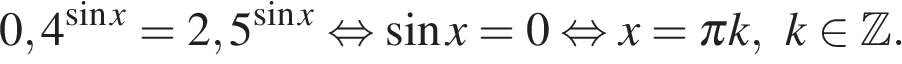
14. В одном основании прямого кругового цилиндра с высотой 3 и радиусом основания 8 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
Решение.
а) Для построения сечения опустим перпендикуляры AM и BN на второе основание цилиндра. Отрезки AM и BN параллельны и равны, значит, ABNM — параллелограмм. Так как прямые AM и BN перпендикулярны основаниям цилиндра и, в частности, прямой AB, параллелограмм ABNM является прямоугольником. Отрезки AN и BM равны как диагонали прямоугольника, что и требовалось доказать.
б) Площадь прямоугольника ABNM равна 3 · 8 = 24. Пусть H — точка пересечения отрезков NM и CD. Отрезок OH равен 
Высота CH пирамиды CABNM равна 
Следовательно, объём пирамиды CABNM равен:
Ответ: б) 
15. Решите неравенство: 
Решение.
Пусть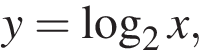 
получаем:
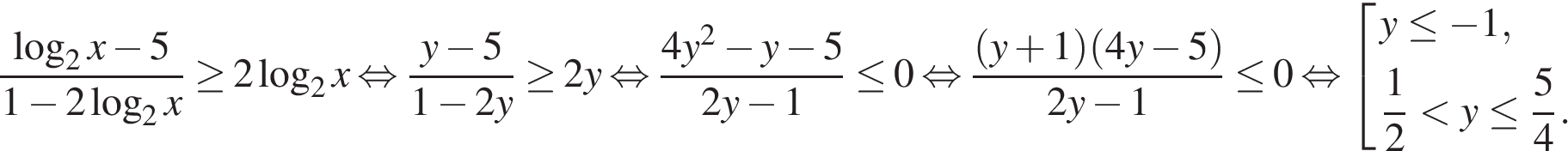
Вернёмся к исходной переменной:
Таким образом, решение исходного неравенства 
Ответ:
16. На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что 
В каком отношении прямая DL делит сторону AB?
Решение.
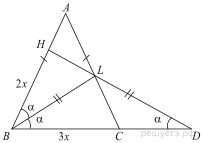
а) Обозначим 
, тогда
, 
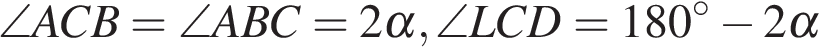поэтому
и треугольник LCD — равнобедренный.
б) Пусть 
пересекает 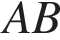в точке 
Тогда
поэтому треугольники HLB и LCB подобны по двум углам. Отсюда 
Поскольку 
, то BC: AB = 3: 2. Пусть AB = 2 x, BC = 3 x.
Поскольку AL: LC = AB: BC, находим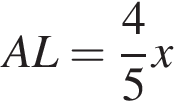 
, 
Тогда 
, значит,
, откуда 
Ответ:21: 4.
17. 1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?
Решение.
Если первый платеж банку Аркадия составил x рублей, то второй составит 2 x рублей, а третий — 3 x рублей, всего 6 x рублей, что равно 2 395 800, т. е. x = 2 395 800: 6 = 399 300. Отсюда: 2 x = 798 600, 3 x =1 197 900.
Пусть в банке Аркадий взял в кредит S рублей.
Тогда его долг 01.03.2011 составил 1,1 S рублей. После первого перечисления Аркадия долг снизился до (1,1 S − 399 300) руб.
01.03.2012 банк начислил проценты на долг Аркадия. Долг Аркадия стал (1,1 S − 399 300) · 1,1 = 1,21 S − 439 230 (руб.)
Аркадий перевел в банк 798 600 руб. Долг снизился до 1,21 S − 439230 − 798600 = 1,21 S − 1237830 (руб.)
01.03.2013 банк начислил проценты на оставшийся долг Аркадия. Долг Аркадия стал (1,21 S − 1237830) · 1,1 = 1,331 S − 1 361 613 (руб.)
Аркадий перевел в банк 1 197 900 руб. Кредит погашен полностью, долга у Аркадия нет.
Значит, 1,331 S − 1 361 613 − 1 197 900 = 0 ⇔ 1,331 S = 2 559 513 ⇔ S = 1 923 000.
Ответ: 1 923 000 рублей.
18. Найдите все значения 
при каждом из которых график функции
пересекает ось абсцисс более чем в двух различных точках.
Решение.
Рассмотрим вспомогательную функцию 
График функции 
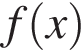пересекает ось абсцисс в трёх или более точках, если уравнение 
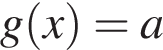имеет более двух различных корней.
Если 
или 
то 
и 
Если 
то 
и 
График функции 
состоит из двух лучей и дуги параболы. На рисунке видно, что уравнение 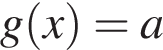имеет более двух корней только если 
Соответствующие значения функции 
равны:
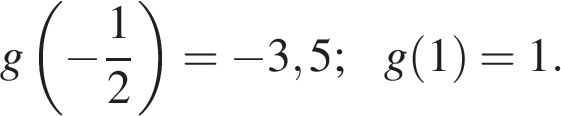
Ответ: 
19. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более 
от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более 
от общего числа учащихся группы, посетивших кино.
а) Могло ли быть в группе 10 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а) и б)?
Решение.
а) Если группа состоит из 4 мальчиков, посетивших только театр, 6 мальчиков, посетивших только кино, и 10 девочек, сходивших и в театр, и в кино, то условие задачи выполнено. Значит, в группе из 20 учащихся могло быть 10 мальчиков.
б) Предположим, что мальчиков было 11 или больше. Тогда девочек было 9 или меньше. Театр посетило не более 4 мальчиков, поскольку если бы их было 5 или больше, то доля мальчиков в театре была бы не меньше 
, что больше 
Аналогично, кино посетило не более 6 мальчиков, поскольку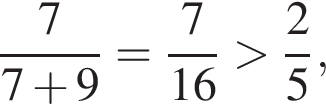 
но тогда хотя бы один мальчик не посетил ни театра, ни кино, что противоречит условию.
В предыдущем пункте было показано, что в группе из 20 учащихся могло быть 10 мальчиков. Значит, наибольшее количество мальчиков в группе — 10.
в) Предположим, что некоторый мальчик сходил и в театр, и в кино. Если бы вместо него в группе присутствовало два мальчика, один из которых посетил только театр, а другой — только кино, то доля мальчиков и в театре, и в кино осталась бы прежней, а общая доля девочек стала бы меньше. Значит, для оценки наименьшей доли девочек в группе можно считать, что каждый мальчик сходил или только в театр, или только в кино.
Пусть в группе 
мальчиков, посетивших театр, 
мальчиков, посетивших кино, и 
девочек. Оценим долю девочек в этой группе. Будем считать, что все девочки ходили и в театр, и в кино, поскольку их доля в группе от этого не изменится, а доля в театре и в кино не уменьшится.
Из условия:
значит, 
Тогда 
, поэтому доля девочек в группе:
Если группа состоит из 4 мальчиков, посетивших только театр, 6 мальчиков, посетивших только кино, и 9 девочек, сходивших и в театр, и в кино, то условие задачи выполнено, а доля девочек в группе равна 
Ответ: а) да: б) 10; в)